A lei da indução aplica-se a circuitos elétricos e como estes podem considerar-se um conjunto de malhas, cada uma com a sua corrente, será aqui analisada para uma espira constituída por um fio condutor de dimensões limitadas, mas de espessura fina, comparada com o seu perímetro de modo que o fio pode ser considerado uma linha para a maior parte dos propósitos. A lei faz intervir dois importantes conceitos que, a seguir, se relembram.

1º Força eletromotriz (f.e.m.)

Trata-se, simplesmente, do trabalho realizado ao longo do circuito pela força eletromagnética que actua sobre a unidade de carga, i.e., é o trabalho da força de Lorentz para carga unitária:

\(\varepsilon =\oint d\vec{l}\cdot \left ( \vec{E}+\vec{V}\wedge \vec{B} \right )\) (1)

Aqui, \(d\vec{l}\) é um pequeno vetor, tangente, em cada ponto, à linha, de grandeza igual ao elemento de comprimento da linha e com o sentido da circulação arbitrada na espira. Por sua vez, \(\vec{E}\) e \(\vec{B}\) são, respetivamente, as intensidades dos campos elétrico e magnético, podendo, qualquer um deles, variar no tempo e no espaço. E \(\vec{V}\) é a velocidade de cada ponto da espira se esta se deslocar no espaço. Notar-se-á que \(\vec{E}\) não pode ser um campo eletrostático, pois que este é o gradiente de um potencial pelo que terá circulação nula numa espira fechada.

2º Fluxo do campo magnético

Imagine-se uma superfície \(\Sigma\) qualquer, aberta e que se apoia sobre a linha. Em cada um dos seus pontos define-se o versor da normal \(\left ( \vec{n} \right )\) cujo sentido está ligado ao sentido da circulação pela regra do saca-rolhas. Nestas condições, o fluxo do campo magnético através da espira é:

\(\Phi \left ( t \right )=\int_{\Sigma}^{}dS\vec{n}\cdot \vec{B}\left ( \vec{r},t \right )\) (2)

O fluxo pode depender do tempo quer porque o campo magnético depende do tempo, quer porque a espira se desloca no espaço cortando linhas de força do campo. Estes dois casos serão analisados adiante.

A lei da indução estabelece a relação entre estes dois conceitos:

\(\varepsilon =-\frac{d\Phi }{dt}\) (3)

O sinal negativo nesta expressão tem uma importância capital. A f.e.m. por si só induz uma corrente na espira a qual, por sua vez, origina um campo magnético e um fluxo que fazem parte das equações anteriores. O sinal indica que tal corrente, pelo seu efeito magnético, se opõe à causa que a originou, i.e., se o fluxo, por exemplo, estiver a aumentar a corrente gerada cria um campo magnético que se opõe àquele aumento de fluxo. É este o conteúdo da lei de Lenz (1834), uma lei qualitativa, mas de grande valor na interpretação de diversos efeitos da indução eletromagnética.

A variação temporal do fluxo na eq. (3) pode ter origem num campo magnético varável no tempo como pode ser devida ao movimento da espira através e um campo magnético estacionário. Estes dois processos são, agora, analisados. Na FIGURA 1, cada ponto da espira, representada por \(C (t)\) num dado instante, desloca-se de \(\vec{V}\delta t\), assumindo uma nova configuração \(C\left ( t+\delta t \right )\) atravessada por um campo magnético que, entretanto, se alterou.

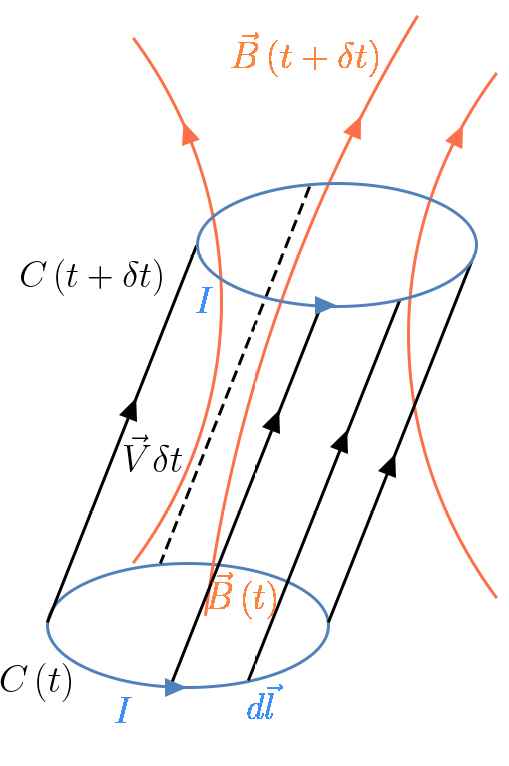
A variação genérica do fluxo através da espira escreve-se:

\(\Phi \left ( t+\delta t \right )-\Phi \left ( t \right )=\int_{\Sigma\left ( t+\delta t \right )}^{}ds\vec{n}\cdot \vec{B}\left ( \vec{r},t+\delta t \right )-\int_{\Sigma\left ( t \right )}^{}ds\vec{n}\cdot\vec{B}\left ( \vec{r},t \right )=\)

\(=\oint_{\Sigma\left ( t+\delta t \right )}^{}ds\vec{n}\cdot \left [ \vec{B}\left ( \vec{r},t+\delta t \right )-\vec{B}\left ( \vec{r},t \right ) \right ]+\left [ \int_{\Sigma\left ( t+\delta t \right )}^{}ds\vec{n}\cdot \vec{B}\left ( \vec{r},t \right )-\int_{\Sigma\left ( t \right )}^{}ds\vec{n}\cdot \vec{B}\left ( \vec{r},t \right ) \right ]\)

No último membro, o primeiro termo representa a variação temporal do fluxo para um campo que variou, mas com a espira imóvel (na sua posição final), pelo que:

\(=\oint_{\Sigma\left ( t+\delta t \right )}^{}ds\vec{n}\cdot \left [ \vec{B}\left ( \vec{r},t+\delta t \right )-\vec{B}\left ( \vec{r},t \right ) \right ]\rightarrow \delta t\int_{\Sigma\left ( t \right )}^{}ds\vec{n}\cdot\frac{\partial \vec{B}\left ( \vec{r},t \right )}{\partial t}\)

O segundo termo representa a variação de fluxo de um campo estacionário (“congelado” no instante inicial) através da espira entre as suas posições final e inicial. Observando a figura, vê-se que a espira nestas posições e o campo de deslocamentos \(\vec{V}\delta t\) definem um cilindro “deformado” no qual a base inferior é a espira na sua posição inicial (com \(- \vec{n}\) versor apontando para o exterior do cilindro) e a base superior é a espira na sua posição final (com \(\vec{n}\) versor apontando para o exterior do cilindro). Ora, deve ser nulo o fluxo do campo \(\vec{B}\left ( \vec{r},t \right )\) através da superfície completa do cilindro, pelo que:

\(\int_{\Sigma\left ( t+\delta t \right )}^{}ds\vec{n}\cdot \vec{B}\left ( \vec{r},t \right )+\int_{\Sigma\left ( t \right )}^{}ds\left ( -\vec{n} \right )\cdot \vec{B}\left ( \vec{r},t \right )+\oint_{C\left ( t \right )}^{}d\vec{l}\wedge \left ( \vec{V}\delta t \right )\cdot \vec{B}\left ( \vec{r},t \right )=0\)

Assim, aquele segundo termo fica:

\(\int_{\Sigma\left ( t+\delta t \right )}^{}ds\vec{n}\cdot \vec{B}\left ( \vec{r},t \right )+\int_{\Sigma\left ( t \right )}^{}ds\vec{n}\cdot \vec{B}\left ( \vec{r},t \right )=-\delta t\oint_{C\left ( t \right )}^{}d\vec{l}\cdot \vec{V}\wedge \vec{B}\left ( \vec{r},t \right )\)

Juntando estas contribuições, obtém-se:

\(\frac{\partial \Phi }{\partial t}=\int_{\Sigma\left ( t \right )}^{}ds\vec{n}\cdot\frac{\partial \vec{B}\left ( \vec{r},t \right )}{\partial t}-\oint_{C\left ( t \right )}^{}d\vec{l}\cdot\vec{V}\wedge \vec{B}\left ( \vec{r},t \right )\)

pelo que a f.e.m. induzida é:

\(\varepsilon =-\frac{d\Phi }{dt}=-\int_{\Sigma\left ( t \right )}^{}ds\vec{n}\cdot\frac{\partial \vec{B}\left ( \vec{r},t \right )}{\partial t}+\oint_{C\left ( t \right )}^{}d\vec{l}\cdot \vec{V}\wedge \vec{B}\left ( \vec{r},t \right )\)

Comparando com a eq. (1), conclui-se:

\(\oint_{C\left ( t \right )}^{}d\vec{l}\cdot\vec{E}=-\int_{\Sigma\left ( t \right )}^{}ds\vec{n}\cdot\frac{\partial \vec{B}}{\partial t}\)

Embora este resultado seja estritamente válido para espiras físicas, constituídas por condutores finos, Maxwell assumiu-a como verdadeira para qualquer linha fechada, no primeiro membro, e qualquer superfície aberta apoiada naquela linha, no segundo membro. Sendo assim, o teorema de Stokes permite transformar o primeiro membro:

\(\oint_{C\left ( t \right )}^{}d\vec{l}\cdot\vec{E}=-\int_{\Sigma}^{}ds\vec{n}\cdot\bigtriangledown \wedge \vec{E}\)

Dada a arbitrariedade da linha e da superfície, obtém-se, assim a equação de Maxwell- Faraday:

\(\bigtriangledown \wedge \vec{E}=-\frac{\partial \vec{B}}{\partial t}\) (4)

Estas considerações não devem ocultar a imensa importância da lei de Faraday. Os dois processos de geração de uma f.e.m. são bem identificados nas figuras seguintes.

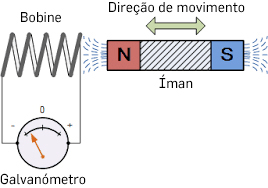
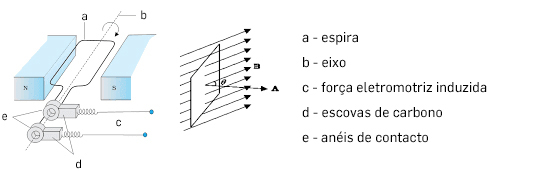
O processo tipificado na FIGURA 3 é, essencialmente, o método de geração de corrente elétrica alternada sinusoidal nas centrais hidroelétricas onde a rotação das espiras do gerador é accionada por uma turbina hidráulica.

Os exemplos seguintes ajudam a clarificar alguns destes importantes resultados.

1º A FIGURA 4 representa um circuito constituído por dois condutores retilíneos verticais (distantes \(l\) ligados, em cima, por uma resistência \((R)\) e, em baixo, por uma barra condutora móvel (massa \(m\)); desprezam-se as resistências elétricas dos condutores verticais e da barra móvel. O dispositivo está mergulhado num campo magnético \(\left ( B_{a} \right )\) uniforme (pontos azuis), perpendicular ao plano da figura e dirigido “para cá” . Permitindo que a barra caia no campo gravítico terrestre, o fluxo do campo \(\Phi \left ( t \right )=B_{a}lz\left ( t \right )\) varia no tempo, gerando uma f.e.m. \(\varepsilon =-B_{a}lv\) que cria uma corrente \(I\left ( t \right )=-\frac{B_{a}lv}{R}\) (o sinal indica que tem o sentido contrário ao da circulação indicado na figura).

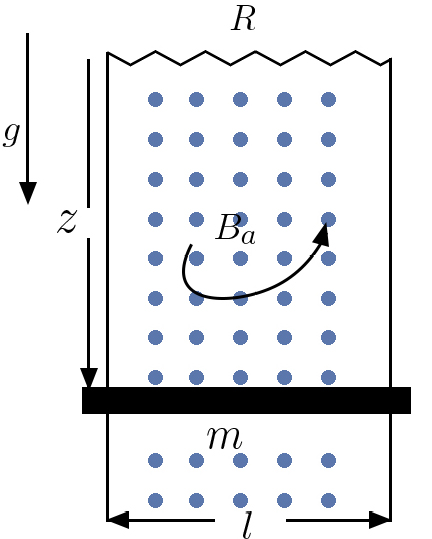
Esta corrente origina, na barra, a força de Laplace, vertical, \(F=IlB_{a}\) de modo que a equação de movimento desta, é:

\(m\frac{dv}{dt}=mg+F=mg-\frac{\left ( B_{a}l \right )^{2}}{R}v\)

Reconhece-se ser a equação de movimento de um grave sujeito a uma força viscosa do tipo de Stokes. Se a barra partir da posição mais alta com velocidade nula, a sua velocidade em qualquer instante posterior é \(v\left ( t \right )=g\tau \left ( 1-e^{-\frac{t}{\tau}} \right )\), onde \(\tau =\frac{mR}{\left ( B_{a}l \right )^{2}}\) é uma constante do tempo; o movimento é praticamente uniforme ao fim de \(3 \tau\), com a velocidade terminal \(g \tau\). O problema, contudo, é um pouco mais complicado porque a corrente cria o seu próprio campo magnético \(B\propto I\) e é, também, por ele actuado, originando uma força de Laplace adicional \(f\propto IB\propto I^{2}\). Percebe-se que esta contribuição poderá ser ignorada para “baixas” intensidades de corrente.

Este dispositivo funciona como um travão eletromagnético com múltiplas aplicações, em particular como elemento adicional de segurança em alguns tipos de elevadores.

2º O disco de Faraday (FIGURA 7).

Um disco circular (raio \(R\)), metálico, roda com velocidade angular \(\left ( \omega \right )\) constante, em torno de um eixo (raio \(r_{0}\ll R\)) perpendicular ao disco e passando pelo seu centro (FIGURA 5). O disco encontra-se mergulhado num campo magnético \(\left ( B_{a} \right )\) constante e uniforme, paralelo ao seu eixo. Atingida a situação estacionária, verifica-se existir uma diferença de potencial elétrico entre o centro do disco e a sua periferia.

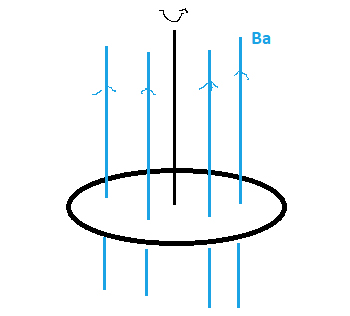
Com efeito, o disco metálico é constituído por iões, que rodam solidariamente com o disco, e eletrões livres. Ambos são actuados pela força \(q\vec{v}\wedge \vec{B}_{a}\), mas só os eletrões se podem mover em relação ao disco, acumulando carga na sua superfície e, desta forma, criando um campo elétrico radial que se torna constante após um período transitório. Nesta situação, a força de Lorentz¹ \(q\left ( \vec{E}+\vec{v}\wedge \vec{B}_{a} \right )\) anula-se, pelo que:

\(E_{r}=-\omega rB_{a}=-\frac{\partial \varphi }{\partial r}\)

Donde a diferença de potencial mencionada:

\(V=\varphi \left ( R \right )-\varphi \left ( r_{0} \right )=\frac{1}{2}\omega B_{a}\left ( R^{2}-r_{0}^{2} \right )=\frac{\omega \Phi }{2\pi}\)

onde \(\Phi \) é o fluxo do campo magnético através do disco. Aquele campo elétrico indica existir uma densidade de carga na superfície do disco:

\(\frac{\rho _{s}}{\varepsilon _{0}}=\frac{1}{r}\frac{d}{dr}\left ( rE_{r} \right )=-2\omega B_{a}\;\; \; \rightarrow \; \; \; \frac{Q}{\varepsilon _{0}}=-2\omega B_{a}\pi R^{2}\)

Carga oposta surge na periferia do disco, como se deduz da descontinuidade do campo elétrico aí verificada:

\(\frac{\rho l}{\varepsilon _{0}}=-E_{r}\left ( R \right )=\omega RB_{a}\; \; \; \rightarrow \; \; \; \frac{Q'}{\varepsilon _{0}}=\omega RB_{a}2\pi R=-\frac{Q}{\varepsilon _{0}}\)

Imagine-se, agora, que se faz passar corrente (intensidade \(I\)) ao longo do eixo, retirando- a, uniformemente, da periferia do disco. Esta corrente distribui-se radialmente no disco, sendo \(i_{s}\left ( r \right )2\pi r=I\). A corrente responde à f.e.m.: \(i_{s}=\sigma _{s}\left ( E_{r}+\omega rB_{a} \right )\), onde \(\sigma _{s}\) é a condutividade superficial (a condutividade do metal multiplicada pela espessura do disco). Então:

\(E_{r}=\frac{I}{2\pi r\sigma _{s}}-\omega rB_{a}=-\frac{\partial \varphi }{\partial r}\)

A diferença de potencial entre a periferia do disco e o seu eixo passa a ser:

\(V=\frac{\omega \Phi }{2\pi}-\frac{I}{2\pi\sigma _{s}}\textrm{log}\left ( \frac{R}{r_{0}} \right )\)

A corrente radial \(i_{s}\), sob acção do campo magnético aplicado, resulta em forças de Laplace \(\vec{i}_{s}\wedge \vec{B}_{a}dS\) distribuídas na superfície do disco. Estas forças têm resultante nula, mas um momento resultante (polo no centro do disco) não nulo e dirigido segundo o eixo de rotação:

\(M_{z}=-\int dSi_{s}\left ( r \right )B_{a}r=-\frac{IB_{a}}{2}\left ( R^{2}-r^{2} \right )=-\frac{I\Phi }{2\pi}\)

Este momento opõe-se ao movimento do disco (lei de Lenz) – é compensado pelo momento exterior do motor que mantem o disco em rotação uniforme, o qual despende, assim, a potência \(\frac{I\Phi }{2\pi}\omega \). Reconhece-se, neste modelo, o princípio de funcionamento dos contadores de eletricidade!

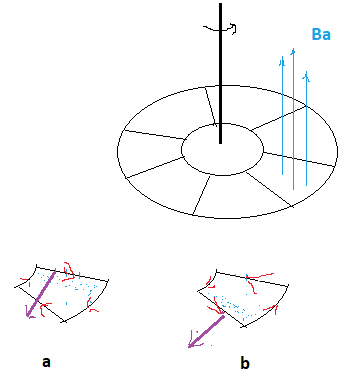
O disco de Faraday (FIGURA 7) é uma variante do anterior: o campo magnético é aplicado apenas numa pequena região do disco, cuja rotação origina correntes (designadas por correntes de Foucault). Para melhor compreensão do seu funcionamento, imagine-se que o disco é constituído por uma série de malhas condutoras (FIGURA 6). Prestando atenção a uma dessas malhas, vê-se que, quando ela penetra na região do campo (FIGURA 6A)), o aumento de fluxo induz uma corrente que se “opõe” ao campo (lei de Lenz), resultando numa força de Laplace que trava o disco; e quando sai da região do campo (FIGURA 6B)), a diminuição do fluxo induz uma corrente de sentido contrário ao anterior, mas que resulta, de novo, numa força de Laplace que se opõe ao movimento. Em ambos os casos o disco é travado na sua rotação, um efeito que subjaz aos “travões de segurança” em veículos pesados.

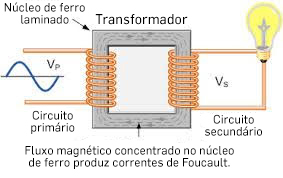
3º Na FIGURA 8, as duas bobinas estão introduzidas nos braços de um núcleo de material ferromagnético, de baixa condutividade, cujo objectivo é concentrar e direccionar as linhas de campo ao longo dos seus braços. Imagine-se que a bobina da esquerda – o primário do transformador – é atravessada por uma corrente sinusoidal \(I\left ( t \right )\). É criado um campo² magnético \(B\left ( t \right )=\frac{N}{l}\mu I\left ( t \right )\), onde N é o número de enrolamentos, \(l\) o comprimento do primário) e \(\mu \) é a permeabilidade magnética do ferro. As linhas de força do campo atravessam a bobina da direita (o secundário), originando um fluxo \(\Phi '\left ( t \right )=N'sB\left ( t \right )\), onde \(N′\) é o seu número de espiras e s é a área da secção das espiras. É, assim, induzida uma f.e.m. no secundário \(\varepsilon '=-\frac{N'N}{l}s\mu \frac{dl}{dt}\) que aparecerá como uma tensão sinusoidal \(\left ( V_{s} \right )\) nos terminais do circuito secundário se este estiver aberto. Esta tensão pode ser maior que a tensão induzida no primário, \(V_{p}=-L\frac{dI}{dt}=-\frac{N^{2}}{l}s\mu \frac{dI}{dt}\), caso em que o dispositivo é um amplificador de tensão, como ser menor – redutor de tensão – dependendo da razão \(\frac{N'}{N}\) ser, respetivamente, maior ou menor do que a unidade. Note-se que no núcleo de ferro (um condutor) as variações de fluxo originam correntes de Foucault que levam ao seu aquecimento.

Coeficientes de auto-indução e de indução mútua

Considerem-se dois circuitos elétricos, independentes, formados por condutores físicos com dimensões finitas (na FIGURA 9, estes circuitos são representados pelas duas espinhas); em cada um é arbitrado um sentido de circulação, desta forma ficando definidos os versores das normais (regra do saca-rolhas) para quaisquer superfícies que se apoiem num e no outro.

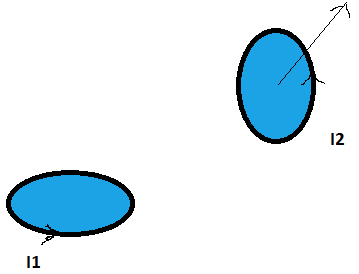
Se os condutores forem percorridos por correntes elétricas, é gerado um campo magnético \(\vec{B}\) em todo o espaço, sobreposição dos campos gerados por cada corrente. A energia magnética associada ao campo, é:

\(U=\frac{1}{2\mu_{0}}\int dV\vec{B}^{2}\) (5)

Esta expressão pode ser transformada noutra equivalente se se usar o potencial vetor magnético:

\(U=\frac{1}{2\mu _{0}}\int dV\vec{B}\cdot \bigtriangledown \wedge \vec{A}=\frac{1}{2\mu_{0}}\int dV\vec{A}\cdot\bigtriangledown \wedge \vec{B}+\frac{1}{2\mu _{0}}\int dV\bigtriangledown \cdot\left ( \vec{A}\wedge \vec{B} \right )\)

O último termo é nulo para correntes localizadas; com efeito, tal termo pode ser transformado no fluxo de \(\vec{A}\wedge \vec{B}\) através de uma superfície esférica gaussiana de raio arbitrariamente grande onde aqueles campos decaem com suficiente rapidez para assegurar o anulamento. Para o outro termo, a equação de Maxwell-Ampère dá:

\(U=\frac{1}{2}\int dV\vec{i}\cdot \vec{A}\) (6)

Aplicando aos dois circuitos, obtém-se:

\(U=\frac{1}{2}\int dV_{1}\vec{i}_{1}\left ( \vec{r}_{1} \right )\cdot \vec{A}_{1}+\frac{1}{2}\int dV_{1}\vec{i}_{1}\cdot \vec{A}_{2}+\frac{1}{2}\int dV_{2}\vec{i}_{2}\cdot\vec{A}_{1}+\frac{1}{2}\int dV_{2}\vec{i}_{2}\cdot\vec{A}_{2}\)

Os dois termos intermédios são iguais:

\(\int dV_{1}\vec{i}_{1}\left ( \vec{r}_{1} \right )\cdot\vec{A}_{2}\left ( \vec{r}_{1} \right )=\frac{\mu_{0}}{4\pi}\int dV_{1}\vec{i}_{1}\left ( \vec{r}_{1} \right )\cdot\int dV_{2}\frac{\vec{i}_{2}\left ( \vec{r}_{2} \right )}{R_{12}}=\int dV_{2}\vec{i}_{2}\left ( \vec{r}_{2} \right )\cdot \vec{A}_{1}\left ( \vec{r}_{2} \right )\)

onde \(R_{12}=\left | \vec{r}_{1}-\vec{r}_{2} \right |\) é a distância entre dois pontos genéricos, um em cada circuito. Como os potenciais são proporcionais às correntes que os originam, a energia do campo pode escreverse sob a forma:

\(U=\frac{1}{2}L_{1}I_{1}^{2}+M_{12}I_{1}I_{2}+\frac{1}{2}L_{2}I_{2}^{2}\) (7)

Esta expressão define os coeficientes de auto-indução de cada circuito \(\left ( L \right )\) e o coeficiente de indução mútua entre os dois circuitos \(\left ( M_{12} \right )\). Como deve ser \(U\geq 0\) quaisquer que sejam as intensidades das correntes, obtém-se:

\(L_{1}L_{2}\geq M_{12}^{2}\) (8)

Em geral, a redução dos circuitos a linhas fechadas (sem espessura) não serve para o cálculo dos coeficientes de auto-indução, porque o potencial vetor diverge nos pontos de tais linhas. Contudo, se esse efeito puder ser ignorado, obtém-se:

\(LI^{2}=I\oint d\vec{l}\cdot \vec{A}=I\int dS\vec{n}\cdot \vec{B}=I\Phi \; \; \; \rightarrow \; \; \; L=\frac{\Phi }{I}\) (9)

Assim, o coeficiente de auto-indução aparece como a razão entre o fluxo através da espira (auto-fluxo) e a intensidade da corrente que o origina. Por exemplo, no primário da FIGURA 8, se apenas se considerar o campo magnético no interior da bobina, tem-se:

\(L\simeq \mu\frac{N^{2}}{l}s\) (10)

O cálculo do coeficiente de indução mútua, porém, é muitas vezes bem aproximado considerando circuitos filiformes, tendo-se:

\(M_{12}=\oint_{C_{1}}^{}d\vec{l}\cdot\frac{\vec{A}_{2}\left ( \vec{r}_{1} \right )}{I_{2}}=\int_{\Sigma_{1}}^{}dS_{1}\vec{n}_{1}\cdot\frac{\vec{B}_{2}\left ( \vec{r}_{1} \right )}{I_{2}}=\frac{\Phi _{12}}{I_{2}}\) (11)

Aqui, \(\Phi _{12}\) é o fluxo através do primeiro circuito do campo magnético gerado pela corrente no segundo circuito. É óbvio que se podem trocar os circuitos neste cálculo resultando na expressão equivalente \(M_{12}=\frac{\Phi _{21}}{I_{1}}\), pelo que:

\(MI_{1}I_{2}=I_{1}\Phi _{12}=I_{2}\Phi _{21}\)

Por exemplo, para as duas bobinas da FIGURA 8, tem-se:

\(M_{12}=\mu\frac{N'N}{l}s\) (12)

Deve notar-se que o coeficiente de indução mútua não depende, apenas, das características geométricas de cada bobina, mas também da distância entre elas, da orientação relativa dos seus eixos e dos sentidos nos enrolamentos. As mesmas bobinas da FIGURA 8, se colocadas com os eixos perpendiculares entre si, determinarão um coeficiente de indução mútua praticamente nulo; e se os enrolamentos forem opostos, este coeficiente é negativo.

Considere-se, de novo, a FIGURA 9 e imagine-se que o circuito 2 se move (como indicado pela seta). Este circuito é actuado pela força de Laplace que realiza o trabalho \(\delta W_{L}=I_{2}\delta \Phi _{21}=I_{1}I_{2}\delta M_{12}\), pois que são consideradas constantes as correntes no cálculo deste trabalho2. Assim, a potência associada à força de Laplace é originada pela variação do coeficiente de indução mútua causada pela alteração de geometria no movimento relativo dos circuitos

\(P_{L}=I_{1}I_{2}\frac{\partial M}{\partial t}\)

Devido ao movimento, variam os fluxos através de qualquer das espiras, gerando forças eletromotrizes que realizam trabalho (Faraday). Para o circuito 1, a potência da f.e.m. induzida é obtida invocando a lei da indução:

\(P_{F}^{\left ( 1 \right )}=-I_{1}\frac{\partial }{\partial t}\left ( L_{1}I_{1}+M_{12}I_{2} \right )=-\frac{1}{2}\frac{\partial }{\partial t}\left ( L_{1}I_{1}^2{} \right )-I_{1}\left [ M_{12}\frac{\partial I_{2}}{\partial t}+I_{2}\frac{\partial M_{12}}{\partial t} \right ]\)

Analogamente, para o circuito 2:

\(P_{F}^{\left ( 2 \right )}=-I_{2}\frac{\partial }{\partial t}\left ( L_{2}I_{2}+M_{12}I_{1} \right )=-\frac{1}{2}\frac{\partial }{\partial t}\left ( L_{2}I_{2}^{2} \right )-I_{2}\left [ M_{12}\frac{\partial I_{1}}{\partial t}+I_{1}\frac{\partial M_{12}}{\partial t} \right ]\)

Somando estas potências, tem-se:

\(P_{L}+P_{F}^{\left ( 1 \right )}+P_{F}^{\left ( 2 \right )}=-\frac{\partial }{\partial t}\left ( \frac{1}{2}L_{1}I_{1}^{2}+\frac{1}{2}L_{2}I_{2}^2{+M_{12}I_{1}I_{2}} \right )=-\frac{dU}{dt}\)

Quer isto dizer que a diminuição, na unidade de tempo, da energia magnética contabiliza todo o trabalho realizado na mesma unidade de tempo pelas forças exercidas pelo campo magnético, sejam elas forças de Laplace actuando sobre circuitos móveis, sejam as f.e.m. induzidas nos circuitos por acção desses movimentos relativos³.

Estão estabelecidos os principais conceitos para se discutirem circuitos elétricos, em corrente contínua ou alternada. Com as noções de capacidade de um condensador⁴ e dos coeficientes de auto-indução e indução mútua ficam definidos os principais termos que intervêm no estudo dos circuitos elétricos de que se ocupa o artigo “Circuitos elétricos”.