Aplicando um campo elétrico a um metal verifica-se o aparecimento de uma corrente elétrica que satisfaz à lei de Ohm (1827):

\(\vec{i}=\sigma \vec{E}\) (1)

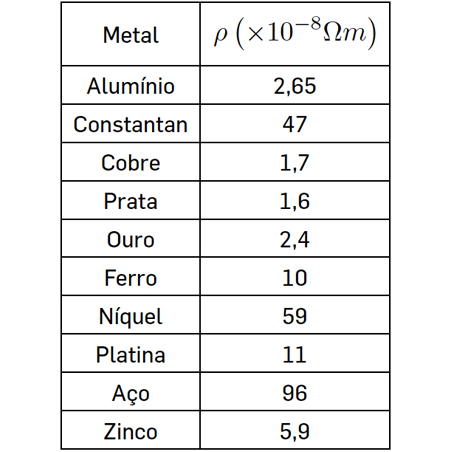
Aqui,   é a condutividade do metal, designando-se por resistividade o seu inverso: \(\rho =\frac{1}{\sigma }\) (unidade S.I. ohm^*m). A tabela seguinte mostra os valores da resistividade, à temperatura ambiente, para alguns metais. A resistividade aumenta com a temperatura, tipicamente da ordem de 0,5%/ K.

A equação (1) exibe claramente uma quebra de simetria por inversão do tempo¹, uma propriedade característica de um fenómeno irreversível. E, de facto, o trabalho realizado pelo campo elétrico em cada segundo e por unidade de volume, é convertido em calor (calor de Joule).:

\(\frac{\delta ^{2}W}{\delta V\delta t}=\vec{i}\cdot \vec{E}=\rho \vec{i}^{2}\) (2)

A FIGURA 2 mostra uma porção de um condutor cilíndrico (raio a, comprimento \(l\)), nas extremidades do qual é aplicada uma diferença de potencial \(V_{A}-V_{B}\). O cilindro é atravessado por uma corrente, de intensidade \(I\), que se distribui uniformemente na secção transversal e ao longo do eixo.

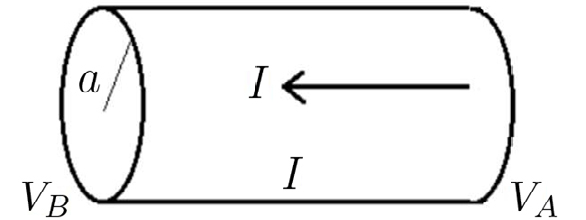
Assim, é \(i=\frac{I}{\pi a^{2}}\) e, da equação (1), resulta:

\(V_{A}-V_{B}=El=\frac{\rho l}{\pi a^{2}}I\equiv RI\) (3)

onde:

\(R=\frac{\rho l}{\pi a^{2}}\) (4)

é a resistência do troço considerado. Esta expressão é generalizável a qualquer outro tipo de secção reta, bastando substituir o denominador pela área dessa secção. Se se considerar um condensador plano cujas armaduras são as bases destes cilindros, a sua capacidade é² \(C=\frac{\varepsilon _{0}\pi a^{2}}{l}\), pelo que \(RC=\varepsilon _{0}\rho\). Ver-se-á que esta relação é mais geral do que aparenta neste exemplo.

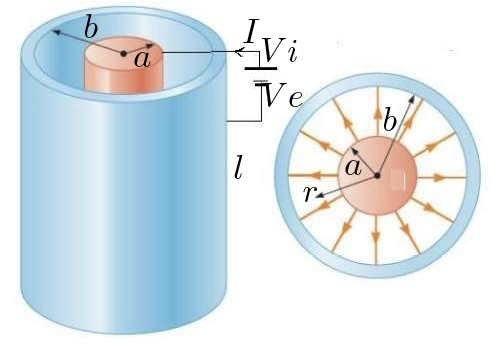
A FIGURA 3 representa duas superfícies cilíndricas coaxiais, de comprimento \(l\) e raios \(a <\)\( b\). O meio entre as superfícies é um condutor \(\left ( \rho \right )\). O cilindro interior é mantido ao potencial \(V_{i}\) e o exterior ao potencial \(V_{e}<\)\(V_{i}\), pelo que existe um campo elétrico radial que origina uma corrente também radial, \(i_{r}=\frac{I}{2\pi rl}\). Pela lei de Ohm, é:

\(E_{r}=pi_{r}=\frac{\rho I}{2\pi rl}=-\frac{\partial \varphi }{\partial r}\rightarrow V_{i}-V_{e}=\frac{\rho I}{2\pi l}\textrm{log}\left ( \frac{b}{a} \right )\)

Assim, a resistência deste condutor é:

\(R=\frac{\rho}{2\pi l}\textrm{log}\left ( \frac{b}{a} \right )\) (5)

Comparando este resultado com a capacidade de um condensador formado pelas mesmas superfícies cilíndricas, obtém-se \(RC=\rho \varepsilon _{0}\), como no exemplo anterior.

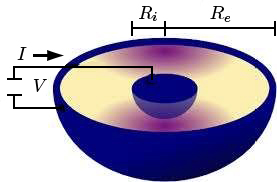
A FIGURA 4 mostra duas superfícies esféricas, concêntricas, de raios \(R_{i}<\)\(R_{e}\). O espaço entre as superfícies é inteiramente ocupado por um meio condutor. Estabelecendo uma diferença de potencial \(V\) entre as esferas, é criado um campo elétrico radial e, portanto, também uma corrente radial \(i_{r}=\frac{I}{4\pi r^{2}}\). A lei de Ohm dá:

\(E_{r}=\rho i_{r}=\frac{\rho I}{4\pi r^{2}}\rightarrow V=\frac{\rho I}{4\pi}\left ( \frac{1}{R_{1}}-\frac{1}{R_{e}} \right )\)

A resistência deste condutor é:

\(R=\frac{\rho}{4\pi}\left ( \frac{1}{R_{i}}-\frac{1}{R_{e}} \right )\) (6)

Comparando com a capacidade de um condensador com a mesma geometria, obtém-se \(RC=\rho \varepsilon _{0}\), como antes.

Esta relação, verificada nestes três exemplos, entre capacidade de um condensador e a resistência de um condutor com a mesma geometria, não é fortuita. Basta lembrar que, para a mesma diferença de potencial (e, portanto, o mesmo campo elétrico), esta determina a carga do condensador (multiplicando aquela por \(C\)) e a corrente no condutor (dividindo aquela por \(R\)). A relação é bastante genérica.

Para todos os exemplos anteriores, é fácil mostrar que o calor de Joule libertado em cada segundo, é:

\(\frac{\delta Q}{\delta t}=RI^{2}\) (7)

A FIGURA 5A) exemplifica a associação de resistências em série: a corrente é a mesma para cada resistência, pelo que a diferença de potencial entre os terminais da série é:

\(V=R_{1}I+R_{2}I+R_{3}I+R_{4}I=\left ( R_{1}+R_{2}+R_{3}+R_{4} \right )I\equiv R_{eq}I\)

onde:

\(R_{eq}=R_{1}+R_{2}+R_{3}+R_{4}\) (8)

é designada por resistência equivalente, uma resistência que pode substituir o conjunto, gerando a mesma tensão para a mesma corrente e libertando o mesmo calor de Joule que é totalmente libertado nas resistências individuais.

A FIGURA 5B) mostra a associação em paralelo das mesmas resistências. Agora, a tensão é a mesma nos terminais de cada resistência, tendo-se:

\(V_{A}-V_{B}=R_{1}I_{1}=R_{2}I_{2}=R_{3}I_{3}=E_{4}I_{4}\)

A corrente que atravessa o conjunto é:

\(I=I_{1}+I_{2}+I_{3}+I_{4}=\left ( V_{A}-V_{B} \right )\left ( \frac{1}{R_{1}}+\frac{1}{R_{2}}+\frac{1}{R_{3}}+\frac{1}{R_{4}} \right )=\frac{V_{A}-V_{B}}{R_{eq}}\)

onde, agora, é:

\(\frac{1}{R_{eq}}=\frac{1}{R_{1}}+\frac{1}{R_{2}}+\frac{1}{R_{3}}+\frac{1}{R_{4}}\) (9)

com o mesmo significado anterior.

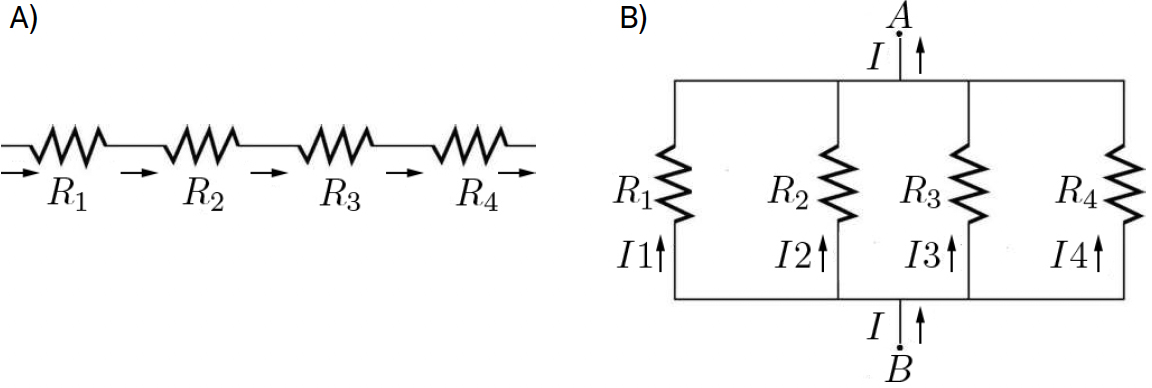
Este conceito de resistência equivalente é muito útil por simplificar a análise de circuitos elétricos.

Um circuito elétrico de corrente contínua (cc) é um conjunto de condutores e uma, pelo menos, força eletromotriz (bateria, pilha). Um nodo é um ponto onde se ligam três ou mais condutores; uma malha é um circuito fechado integrado no circuito elétrico. Há duas maneiras distintas de tratar as correntes. Numa, é atribuída uma corrente a cada ramo (i.e., o condutor que liga dois nodos consecutivos) e escrever que a soma algébrica das correntes é nula em cada nodo (primeira lei de Kirchhoff). Na outra, atribuem-se correntes de malha, reduzindo significativamente o número de incógnitas, ficando automaticamente satisfeita aquela lei. A segunda lei de Kirchhoff, comum aos dois métodos, estabelece que a soma algébrica das quedas de tensão em cada malha iguala a soma algébrica das f.e.m. presentes nessa malha.

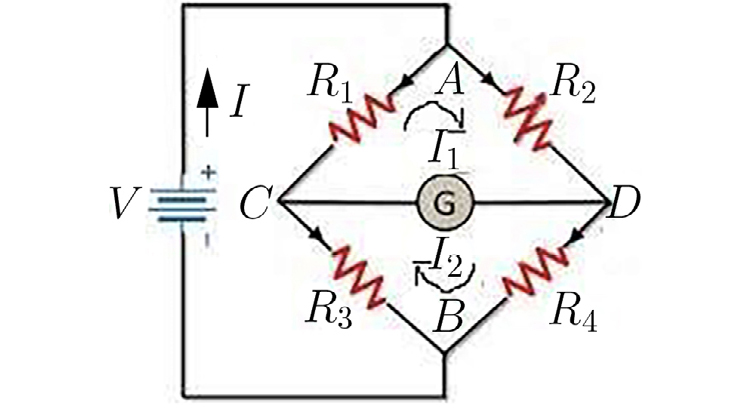
A FIGURA 6 representa a ponte de Wheatstone, um dispositivo para medir resistências elétricas. A ponte diz-se em equilíbrio quando não passar corrente através do amperímetro G (de resistência interna r). O circuito é facilmente analisado com as três correntes de malha identificadas na figura:

\(\begin{matrix} V=R_{1}\left ( I-I_{1} \right )+R_{3}\left ( I-I_{2} \right )\\ 0=R_{1}\left ( I_{1}-I \right )+R_{2}I_{1}+r\left ( I_{1}-I_{2} \right )\\ 0=r\left ( I_{2}-I_{1} \right )+R_{4}I_{2}+R_{3}\left ( I_{2}-I \right ) \end{matrix}\)

Este sistema é resolvido sem dificuldades; a corrente que passa no galvanómetro é \(I_{1}-I_{2}\propto R_{1}R_{4}-R_{2}R_{3}\). Se \(R_{2}\) for um reóstato, a sua resistência pode ser ajustada até a ponte equilibrar, i.e., \(R_{1}R_{4}-R_{2}R_{3}=0\) o que permite medir, por exemplo, \(R_{4}\) se as outras resistências forem conhecidas.

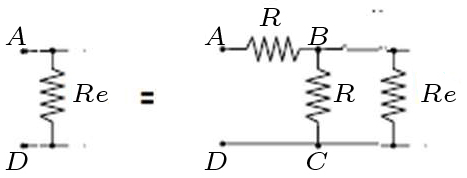
A FIGURA 7 mostra uma ligação de resistências “em cascata” infinita. Contudo, a resistência \(R_{eq}\) medida a partir dos terminais AD é finita. Com efeito, a resistência da cascata a jusante de BC é igual à resistência da cascata completa (FIGURA 8). Então:

\(R_{eq}=R+\frac{RR_{eq}}{R+R_{eq}}\rightarrow R_{eq}=\frac{1+\sqrt{5}}{2}R\)

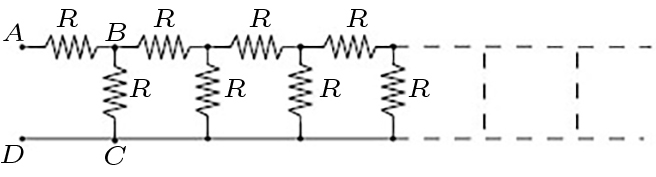
O aparecimento da razão dourada \(\alpha=\frac{1+\sqrt{5}}{2}\) não é fortuito, como se verá a seguir. A FIGURA 9 mostra a cascata de resistências, agora finita e fechada por uma resistência \(R'\).

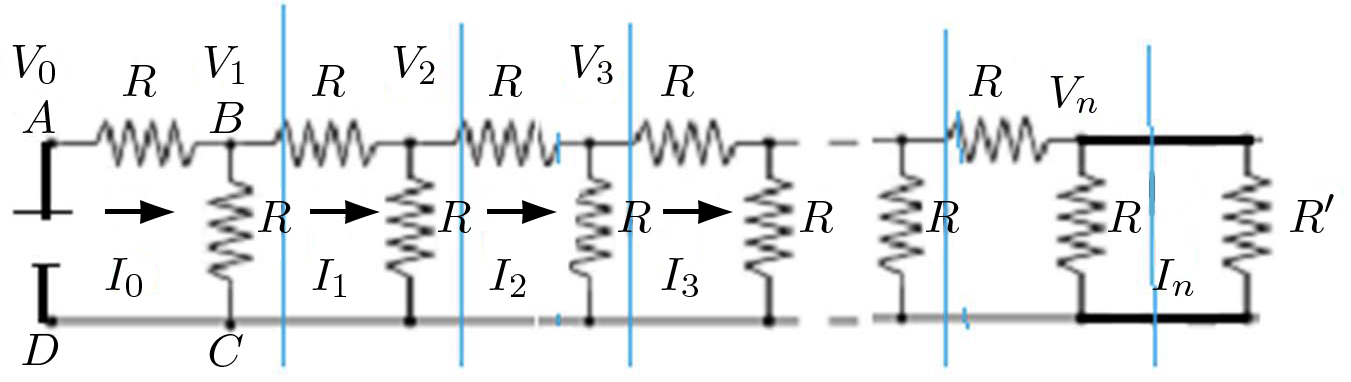
O potencial é nulo em todo o condutor inferior e, no superior, são indicados os potenciais em cada nodo. As linhas azuis mostram que existe um elemento repetitivo designado por quadripolo², que se reproduz na FIGURA 10.

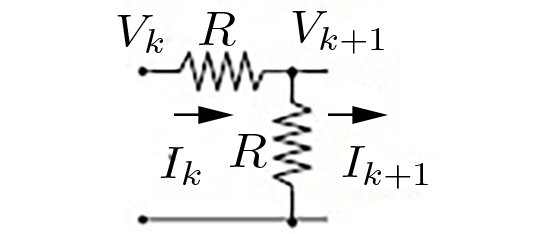
Um quadripolo relaciona linearmente as variáveis de entrada (tensão e corrente) com as variáveis de saída, definindo, dessa forma, a matriz de transferência:

\(\begin{matrix} V_{k}=V_{k+1}+RI_{k}\\ V_{k+1}=R\left ( I_{k}-I_{k+1} \right ) \end{matrix}\)

A matriz de transferência \(T\) obtém-se facilmente a partir das relações anteriores:

\(\begin{matrix} V_{k}=2V_{k+1}+RI_{k+1} & & \\ & \rightarrow & \begin{bmatrix} V_{k}\\ RI_{k} \end{bmatrix}=\begin{bmatrix} 2 & 1\\ 1 & 1 \end{bmatrix}\begin{bmatrix} V_{k+1}\\ RI_{k+1} \end{bmatrix}\equiv T\begin{bmatrix} V_{k+1}\\ RI_{k+1} \end{bmatrix}\\ RI_{k}=V_{k+1}+RI_{k+1} & & \end{matrix}\)

Da FIGURA 9, conclui-se que estas relações são válidas para \(k = 0, 1, ..., n − 1\). Então:

\(\begin{bmatrix} V_{0}\\ RI_{0} \end{bmatrix}=T^{n}\begin{bmatrix} V_{n}\\ RI_{n} \end{bmatrix}=T^{n}\begin{bmatrix} R'\\ R \end{bmatrix}I_{n}\) (10)

Aqui, a última igualdade resulta do fecho da cadeia através da resistência \(R′\).

A matriz de transferência é real e simétrica. Logo, diagonalizável. Os seus valores e vectores próprios são ortogonais e normalizados à unidade, ficam:

\(t_{+}=1+\alpha\; \; \; \; \; v_{+}=\frac{1}{\sqrt{\alpha ^{2}+1}}\begin{bmatrix} \alpha\\ 1 \end{bmatrix}\)

\(t_{-}=1-\alpha\; \; \; \; \; v_{-}=\frac{1}{\sqrt{\alpha ^{2}+1}}\begin{bmatrix} -\alpha\\ 1 \end{bmatrix}\)

Daqui obtém-se:

\(T^{n}=\frac{1}{\sqrt{5}}\left \{ t_{+}^{n}\begin{bmatrix} \alpha & 1\\ 1 & \frac{1}{\alpha} \end{bmatrix}+t_{-}^{n}\begin{bmatrix} \frac{1}{\alpha} & -1\\ -1 & \alpha \end{bmatrix} \right \}\)

Substituindo na equação (10), resulta:

\(\frac{V_{0}}{RI_{0}}=\frac{\alpha R'+R+\left ( \frac{t_{-}}{t_{+}} \right )^{2}\left ( \frac{R'}{\alpha}-R \right )}{R'+\frac{R}{\alpha}+\left ( \frac{t_{-}}{t_{+}} \right )^{n}\left ( -R'+\alpha R \right )}\)

Vê-se agora que a escolha \(R'=\alpha R\) anula qualquer dependência no tamanho da cascata e determina \(\frac{V_{0}}{RI_{0}}=\alpha\), como se tinha encontrado atrás.

Associação de condensadores e de bobinas

A FIGURA 11 mostra dois condensadores ligados em série e que se imagina inseridos num circuito elétrico. Por simples conservação de carga, estão ambos igualmente carregados. Ora:

\(V_{A}-V_{C}=V_{A}-V_{S}+V_{S}-V_{C}=\frac{Q}{C_{1}}+\frac{Q}{C_{2}}\equiv \frac{Q}{C_{eq}}\)

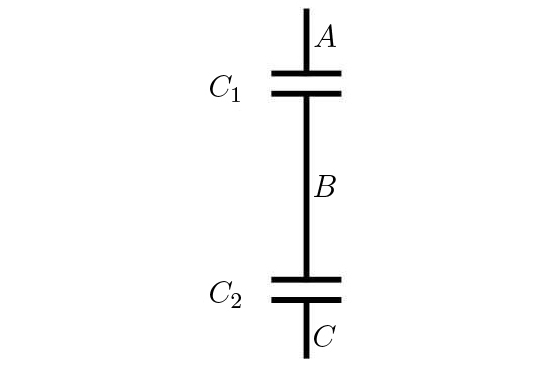
A expressão define a capacidade equivalente do conjunto, i.e., a capacidade de um único condensador que apresenta a mesma carga para a mesma diferença de potencial:

\(\frac{1}{C_{eq}}=\frac{1}{C_{1}}+\frac{1}{C_{2}}\) (11)

Na FIGURA 12, os mesmos condensadores estão ligados em paralelo. Agora, a queda de tensão é a mesma em cada condensador:

\(V_{A}-V_{S}=\frac{Q_{1}}{C_{1}}=\frac{Q_{2}}{C_{2}}\)

A carga total armazenada no conjunto é

\(Q=Q_{1}+Q_{2}=\left ( V_{A}-V_{S} \right )\left ( C_{1}+C_{2} \right )\equiv C_{eq}\left ( V_{A}-V_{S} \right )\)

A capacidade equivalente, com o mesmo significado atrás dado, é a soma das capacidades:

\(C_{eq}=C_{1}+C_{2}\) (12)

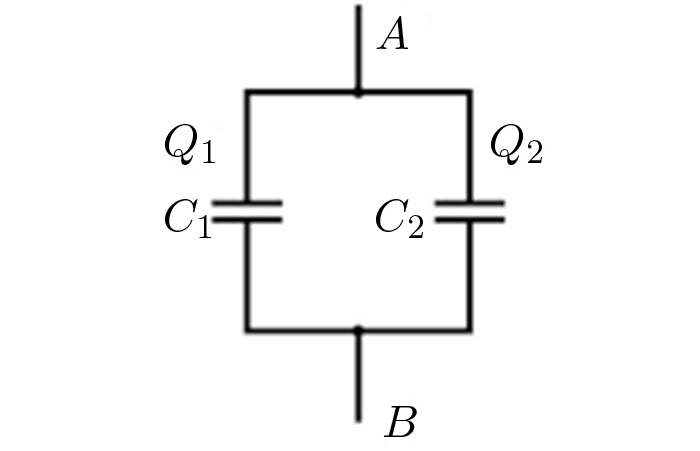
Em ambos os casos, a energia eletrostática acumulada no conjunto é igual à acumulada na capacidade equivalente. Note-se que as expressões para a capacidade equivalente apresentam resultados cruzados com os obtidos para a associação de resistências – tal não é de estranhar se se atender ao resultado \(RC=\rho \varepsilon_{0}\) antes encontrado em diversos exemplos.

A FIGURA 13 representa uma associação em série de bobinas em repouso. O fluxo magnético através das duas bobinas é³:

\(\Phi =L_{1}+L_{2}I+2M_{12}I\)

Então, a f.e.m. desenvolvida entre os terminais A e B é:

\(E=-\frac{d\Phi }{dt}=-\left ( L_{1}+L_{2}+2M_{12} \right )\frac{dI}{dt}\equiv -L_{eq}\frac{dI}{dt}\)

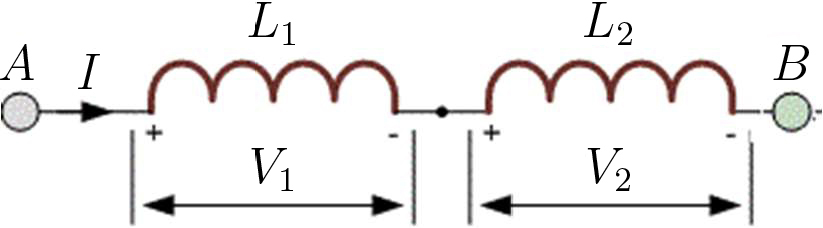
O conjunto comporta-se como uma única bobina com o coeficiente de auto-indução equivalente:

\(L_{eq}=L_{1}+L_{2}+2M_{12}\) (13)

A FIGURA 14 exibe a associação em paralelo das mesmas bobinas. A f.e.m. desenvolvida entre os terminais A e B é a mesma quer se utilize um ou outro ramo para o seu cálculo:

\(\begin{matrix} E=-L_{1}\frac{dI_{1}}{dt}-M_{12}\frac{dI_{2}}{dt}\\ E=-L_{2}\frac{dI_{1}}{dt}-M_{12}\frac{dI_{1}}{dt} \end{matrix}\)

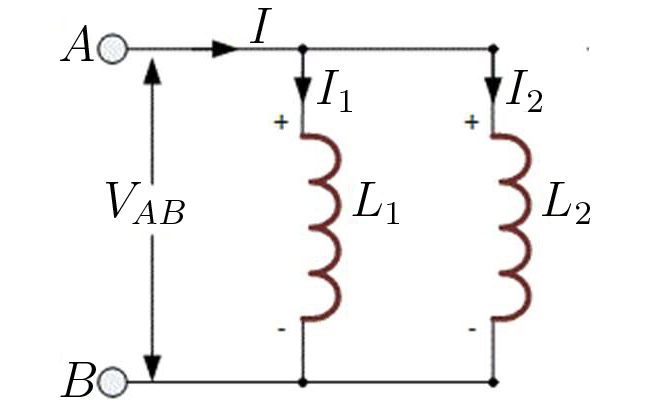
Resolvendo em ordem às correntes em cada ramo e notando que a corrente \(I\) que entra no circuito é a soma daquelas, tem-se:

\(\frac{dI}{dt}=\frac{dI_{1}}{dt}+\frac{dI_{2}}{dt}=-\left [ \frac{L_{1}+L_{2}-2M_{12}}{L_{1}L_{2}-M_{12}^{2}} \right ]E\equiv -\frac{E}{L_{eq}}\)

do que define a impedância equivalente para esta associação:

\(L_{eq}=\frac{L_{1}L_{2}-M_{12}^{2}}{L_{1}+L_{2}-2M_{12}}\) (14)

É, pela equação anterior, o coeficiente de auto indução de uma bobina que apresenta nos seus terminais a mesma tensão para a mesma corrente \(I\).

Em ambas associações, a energia acumulada pelas bobinas é a mesma que na “bobina equivalente”. Deve-se notar que o coeficiente de indução mútua não é necessariamente o mesmo nos dois casos pois que depende da distância e orientação relativa das duas bobinas.

Se este coeficiente puder ser ignorado, então as regras para a impedância equivalente são as mesmas que para a associação de resistências. É mesmo comum ignorar o coefi - ciente de indução mútua nestas definições e introduzi-lo como um elemento adicional na análise de circuitos elétricos.

Impedâncias

Resistências, condensadores e bobinas são os elementos principais de circuitos elétricos quando tensões e correntes variam no tempo, como é o caso dos circuitos em corrente alternada (ac). Nestes, as f.e.m. e correntes variam sinusoidalmente no tempo o que permite introduzir a representação complexa pois que aqueles elementos originam relações lineares entre tensões e correntes. As leis de Kirchhoff são válidas em cada instante: em particular, para cada malha, a soma das f.e.m. quer externamente aplicadas quer originadas na lei da indução de Faraday, igualam a soma das quedas de tensão ao longo da malha. No que se segue, aceita-se que foi ultrapassado o período transitório após se activar o circuito.

A FIGURA 15 representa um simples circuito com os elementos em série⁴. A fonte externa aplica uma tensão \(V_{S}\left ( t \right )\), obtendo-se, para a malha:

\(V_{S}\left ( t \right )-L\frac{dI}{dt}=\frac{Q}{C}+RI\)

\(I=\frac{dQ}{dt}\)

Aceitando ser \(V_{S}\left ( t \right )=V_{0}\textrm{cos}\left ( \omega t \right )=\textrm{Re}\left ( V_{0}e^{i\omega t} \right )\), esta representação complexa pode ser usada para a carga e corrente, sob a condição de, no fim dos cálculos, serem tomadas as respectivas partes reais.

Assim, obtém-se das expressões acima, após eliminar a carga na primeira equação:

\(V_{0}=\left ( i\omega L+\frac{1}{i\omega C}+R \right )I\equiv Z\left ( \omega \right )I\)

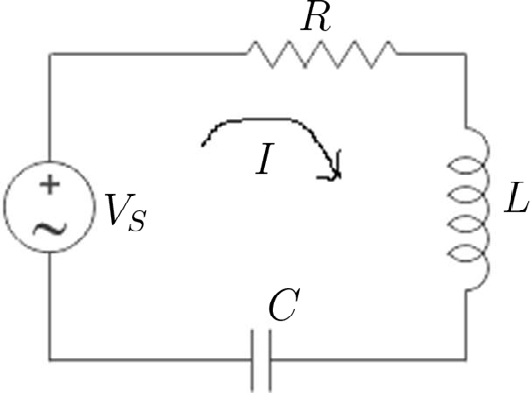
Aqui, \(Z\left ( \omega \right )\) é designada por impedância do circuito, um conceito inventado por Steinmetz que, neste caso, se escreve:

\(Z\left ( \omega \right )=i\omega L+\frac{1}{i\omega C}+R\)

Ora, observando o circuito, vê-se que resistência, bobina e condensador estão em série (são percorridos pela mesma corrente) e, observando a expressão da impedância vê-se que é a soma de três termos, como aconteceria com resistências em série, o que leva a atribuir as seguintes impedâncias a cada um daqueles elementos:

resistência \(\rightarrow \; \; \; \; \; R\)

bobina \(\rightarrow \; \; \; \; \; i\omega L\)

condensador \(\rightarrow \; \; \; \; \; \frac{1}{i\omega C}\)

Nestas condições, as associações, atrás consideradas em série ou paralelo de condensadores ou bobinas (ignorando o coeficiente de indução mútua) conduzem a correspondentes leis de associação de impedâncias idênticas às que se obtiveram para resistências e, dessa maneira, a análise de circuitos ac é idêntica à estudada em circuitos cc.

Regressando ao circuito na FIGURA 15, a potência despendida pelo gerador é \(P\left ( t \right )=V_{S}\left ( t \right )I\left ( t \right )\). Ora, \(I\left ( t \right )=\textrm{Re}\left [ \frac{V_{0}e^{i\omega t}}{Z\left ( \omega \right )} \right ]\). Defina-se \(Z\left ( \omega \right )=\left | Z\left ( \omega \right ) \right |e^{i\alpha \left ( \omega \right )}\) o que origina \(I\left ( t \right )=\frac{V_{0}}{\left | Z\left ( \omega \right ) \right |}\textrm{cos}\left ( \omega t-\alpha\left ( \omega \right ) \right )\). Em geral, define-se a potência fornecida pela média de \(P\left ( t \right )\) sobre um ciclo de vibração:

\(P=\frac{1}{T}\int_{0}^{T}dtP\left ( t \right )=\frac{1}{T}\int_{0}^{T}dt\frac{V_{0}^{2}}{\left | Z\left ( \omega \right ) \right |}\textrm{cos}\left ( \omega t \right )\textrm{cos}\left ( \omega t -\alpha \left ( \omega \right )\right )=\frac{\left | V_{0} \right |}{2\left | Z\left ( \omega \right ) \right |}\textrm{cos}\left ( \alpha \left ( \omega \right ) \right )\)

Este resultado identifica-se com a expressão seguinte:

\(P=\frac{1}{2}\textrm{Re}\left [ V_{0}I^{*} \right ]=\frac{\left [ I \right ]^{2}}{2}\textrm{Re}\left [ Z\left ( \omega \right ) \right ]\geq 0\) (15)

É habitual dar a esta expressão uma forma idêntica à obtida em cc, definindo-se, para isso, a tensão e corrente eficazes, i.e., \(V_{ef}=\frac{V_{0}}{\sqrt{2}}\) e \(I_{ef}=\frac{\left | I \right |}{\sqrt{2}}\). A habitual tensão doméstica de 230V é uma tensão eficaz, uma observação importante para aferir se um dispositivo elétrico aguenta a tensão máxima (que é, portanto, \(\sqrt{2}\) vezes maior).

A ponte de Wheatstone (FIGURA 6), com as resistências nos ramos substituídas por impedâncias, pode ser analisada exatamente como antes, mas nem sempre o equilíbrio é possível. De facto, a condição \(Z_{1}Z_{4}=Z_{2}Z_{3}\) nunca é satisfeita se, por exemplo, \(Z_{1}=R_{1},Z_{3}=R_{3}\) e \(Z_{2}=R_{2},Z_{4}=i\omega L\) ou \(\frac{1}{i\omega C}\). Mas o equilíbrio já é possível se \(Z_{2}=i\omega L,Z_{3}=\frac{1}{i\omega C}\), vindo \(R_{1}R_{4}=\frac{L}{C}\). É mais utilizada a ponte de Anderson (FIGURA 17) que mede, simultaneamente, uma resistência e uma capacidade ou coeficiente de auto-indução.

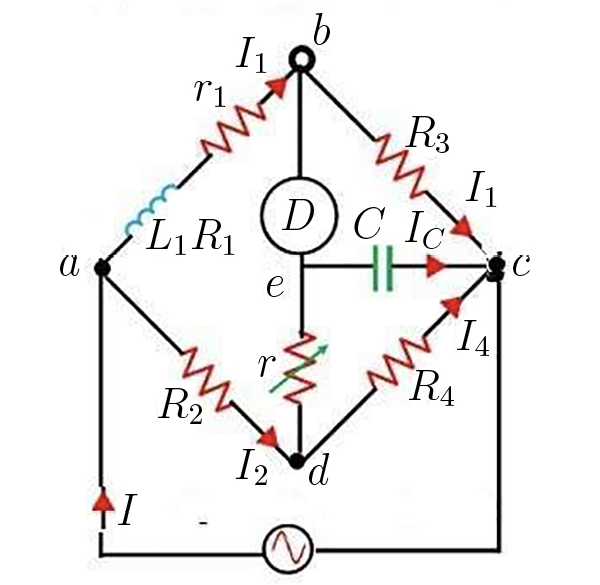
A ponte fica equilibrada quando o detetor D não acusar passagem de corrente, i.e., \(V_{b}=V_{e}\). Nestas condições, a corrente em abc é \(I_{1}\) e tem-se \(V_{c}-V_{a}=I_{1}\left ( R_{1}+r_{1}+\omega L_{1}+R_{3} \right )\). Esta mesma diferença de potencial vigora para adc, i.e., \(V_{c}-V_{a}=I_{2}\left ( R_{2}+\frac{R_{4}\left ( r+\frac{1}{i\omega C} \right )}{R_{4}+r+\frac{1}{i\omega C}} \right )\), ficando assim estabelecida uma primeira relação entre as correntes \(I_{1}\) e \(I_{2}\). Uma segunda relação resulta de \(V_{b}-V_{a}=V_{e}-V_{a}\), i.e., \(I_{1}\left ( R_{1}+r_{1}+i\omega L_{1} \right )=I_{2}R_{2}+rI_{c}\). Ora \(I_{2}=I_{c}+I_{4}\) e \(I_{C}\left (r+ \frac{1}{i\omega C} \right )=I_{4}R_{4}\), o que determina, em particular, \(I_{C}\) que, substituída na igualdade anterior, estabelece a segunda relação entre \(I_{1}\) e \(I_{2}\). Das duas relações, obtém-se a condição de equilíbrio da ponte que é independente da frequência:

\(R_{1}=\frac{R_{2}R_{3}}{R_{4}}-r_{1}\)

\(\frac{L_{1}}{C}=R_{3}\left ( r+R_{2}+\frac{rR_{2}}{R_{4}} \right )\)

A primeira equação é a mesma que para uma ponte de Wheatstone, o que não deve admirar porque a esta se reduz a de Anderson para \(\omega=0\). Aquela equação permite medir \(R_{1}\) se as resistências no segundo membro forem todas conhecidas. A segunda equação determina o coeficiente de auto-indução da bobina ou a capacidade do condensador.

A condição de equilíbrio estabelece uma relação entre impedâncias, desdobrando-se, pois, em duas equações quando se separam, no resultado final, a partes real e imaginária. Ora, a parte imaginária dos elementos na ponte está sempre associada com a frequência, o que justifica a independência na frequência das relações de equilíbrio.

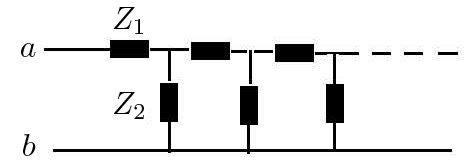
A FIGURA 17 representa uma cascata infinita de impedâncias. A sua análise é idêntica à efetuada com resistências, obtendo-se facilmente a impedância equivalente:

\(Z_{eq}=\frac{1}{2}\left ( Z_{1}\pm \sqrt{Z_{1}^{2}+4Z_{1}Z_{2}} \right )\)

Só são aceitáveis soluções com \(\textrm{Re}\left ( Z_{eq} \right )\geq 0\). Considerando, por exemplo⁴, \(Z_{1}=i\omega L\) e \(Z_{2}=\frac{1}{i\omega C}\), tem-se \(Z_{eq}=\frac{1}{2}\left ( i\omega L\pm \sqrt{\frac{4L}{C}-\omega^{2}L^{2}} \right )\). Assim, para \(\omega\leq 2\sqrt{\frac{1}{LC}}\) só existe uma raíz e há lugar a dissipação. Esta não existe para frequências superiores àquele limite, funcionando a cascata como um filtro passa-alto. Trocando as impedâncias, resulta \(Z_{eq}=\frac{1}{2}\left ( \frac{1}{i\omega C}\pm \sqrt{\frac{4L}{C}-\frac{1}{\omega^{2}C^{2}}} \right )\), havendo dissipação para \(\omega\geq \frac{1}{2\sqrt{LC}}\) altas frequências, i.e., a cascata funciona como um filtro passa-baixo. Mas como pode uma associação de bobinas e condensadores originar dissipação? A resposta, em ambos os casos, reside no facto de o gerador estar sempre a debitar energia porque esta se propaga ao longo da cadeia infinita.

Efeito pelicular

Num condutor onde se estabeleça uma corrente alternada, é gerado um campo magnético que actua sobre a corrente empurrando-a para a superfície do condutor. Este efeito pelicular depende da frequência imposta à corrente, designando-se por profundidade pelicular a distância próxima da superfície onde a corrente preferencialmente se situa. Um modelo simples captura a essência do fenómeno. Imagine-se um condutor que preenche totalmente o espaço acima do plano \(xy\). Para uma corrente paralela a este plano, a sua densidade \(i_{x}\) não pode depender de \(x\), pela lei de conservação de carga, nem de \(y\) por simetria. Assim considerar-se-á ix (z, t), o que origina, por sua vez, um potencial vectorial \(A_{x}\left ( z,t \right )\), satisfazendo¹:

\(\frac{1}{c^{2}}\frac{\partial ^{2}A_{x}}{\partial t^{2}}-\frac{\partial ^{2}A_{x}}{\partial z^{2}}=\mu_{0}i_{x}\)

Aqui, \(c\) deve ser interpretado como a velocidade da luz no metal e \(\mu_{0}\) deve, também, corresponder à permeabilidade magnética do condutor, mas estas observações serão ignoradas no que segue. Ora, pela lei de Ohm, é \(i_{x}=\sigma E_{x}\), onde \(\sigma\) é a condutividade do condutor que, em geral, depende da frequência aplicada mas que aqui, para simplificar, se considerará constante; o campo elétrico, para além do aplicado pelo gerador, tem a parte induzida pela variação no tempo do campo magnético gerado pela corrente. É este que agora se pretende considerar para o que basta recordar¹ a relação \(E_{x}=-\frac{\partial A_{x}}{\partial t}\). Assim, a equação anterior fica:

\(\frac{1}{c^{2}}\frac{\partial ^{2}A_{x}}{\partial t^{2}}-\frac{\partial ^{2}A_{x}}{\partial z^{2}}=-\mu_{0}\sigma \frac{\partial A_{x}}{\partial t}\)

Para corrente variando sinusoidalmente no tempo, tem-se \(A_{x}\left ( z,t \right )=e^{i\omega t}f\left ( z \right )\), obtendo- se:

\(\frac{d^{2}f}{dz^{2}}+k^{2}f=0\) (16)

com:

\(k^{2}=\frac{\omega^{2}}{c^{2}}-i\mu _{0}\sigma \omega\)

Para os metais, o primeiro termo, no segundo membro, só é comparável ao segundo termo para frequências da ordem de 10¹⁸ Hz. Assim, para frequências inferiores a esta, é: \(k\simeq \pm \frac{1-i}{\sqrt{2}}\sqrt{\mu_{0}\sigma \omega}\equiv \pm \frac{1-i}{\delta }\), com \(\delta =\sqrt{\frac{2}{\mu_{0}\sigma \omega}}\). Então, a solução da equação (16) que se anula para z = + , é:

\(f\left ( z \right )\propto e^{-\frac{z}{\delta }}\textrm{cos}\left ( \frac{z}{\delta } \right )\)

A corrente \(i_{x}=-i\omega \sigma e^{i\omega t}f\left ( z \right )\) decai numa distância da ordem de \(\delta \), o comprimento de penetração pelicular. Para os condutores da tabela acima inserida, é \(\delta \sim \) 1cm para \(\omega \sim \) 100 rad/s.