A força eletrostática entre partículas eletricamente carregadas é descrita pela Lei de Coulomb (1783)1, 2, enquanto a Lei da Gravitação Universal de Newton (1687)3, 4 expressa a força gravitacional entre partículas massivas. Apesar dessas forças terem naturezas distintas, as duas leis descrevem forças de interação entre partículas que apresentam características em comum: elas envolvem o produto de uma propriedade intrínseca das partículas envolvidas (carga em um caso, massa no outro) e apresentam uma dependência que varia com inverso do quadrado da distância que as separam. No entanto, as forças gravitacionais são sempre atrativas, enquanto as forças eletrostáticas podem ser atrativas ou repulsivas, dependendo do tipo de carga envolvida (negativa e/ou positiva).

As forças eletrostática e gravitacional atuam a distância por intermédio da ação de um campo. Os campos elétrico e gravitacional podem ser compreendidos como uma região de influência no espaço gerada pelas cargas e massas, respetivamente. Dessa forma, o conceito de campo é muito útil para a determinação da influência das cargas e massas sobre os seus arredores. Como as forças eletrostática e gravitacional são expressas por equações similares, os campos elétrico e gravitacional também o são5, 6.

Apesar da Lei de Coulomb e da Lei da Gravitação Universal fornecerem um suporte necessário para determinar o campo elétrico \(\vec{E}\) de uma distribuição contínua de cargas e o campo gravitacional \(\vec{g}\) de uma distribuição contínua de massas, respetivamente, muitas vezes, as integrais que envolvem os cálculos do campo podem ser complexas, mesmo para casos razoavelmente simples. Nesse sentido, a Lei de Gauss da Eletrostática (1867) permite determinar o campo elétrico \(\vec{E}\) gerado por cargas elétricas. Esta lei é uma das quatro Equações de Maxwell e é equivalente a Lei de Coulomb, porém, seu uso facilita e simplifica a resolução de problemas que possuem elevado grau de simetria (ex: plana, axial ou esférica). A Lei de Gauss foi formulada inicialmente para a Eletrostática, mas devido a semelhança entre os campos elétrico e gravitacional, ela apresenta um análogo para a Gravitação.

A Lei de Gauss da Eletrostática1, 2 estabelece uma relação entre o fluxo de campo elétrico \(\Phi _E\) através de uma superfície imaginária fechada (conhecida como gaussiana) e a carga elétrica \(q\) existente no interior dessa mesma superfície. Essa leié expressa por:


\(\oint \vec{E}.d\vec{S}=\frac{q}{\varepsilon _{0}}\) (1)


onde \(\varepsilon _0=8,85\times 10^{-12}F/m\) é a permissividade elétrica do vácuo e \(d\vec{S}\) é o vetor elemento de área infinitesimal, o qual possui a mesma direção do vetor normal à superfície \(\left ( d\vec{S}=dS\hat{n} \right )\).

Aplicando o Teorema da Divergência na equação (1) e considerando uma distribuição volumétrica de carga, tem-se que:


\(\int \left ( \vec{\bigtriangledown }. \vec{E} \right )dV=\frac{1}{\varepsilon _0}\int \rho_q dV\) (3)


Dessa forma, obtém-se a Lei de Gauss da Eletrostática em seu formalismo diferencial:


\(\vec{\bigtriangledown }.\vec{E}=\frac{\rho _q}{\varepsilon _0}\) (3)


tal que \(\rho_q\) é a densidade da distribuição volumétrica de carga

Pode-se notar que a equação (3) evidencia o fato de que cargas elétricas produzem campos elétricos convergentes e divergentes.

De maneira análoga, a Lei de Gauss da Gravitação7, 8 determina uma relação entre o fluxo de campo gravitacional \(\Phi _G\) através de uma superfície gaussiana e a massa \(m\) contida no interior dessa mesma superfície. Essa lei é dada por:


\(\oint \vec{g}.d\vec{S}=-4\pi Gm\), (4)


tal que \(G = 6, 67 \times 10^{-11}m^{3}\textup{kg}^{-1}s^{-2}\) é a constante da gravitação universal e \(d\vec{S}\) é o vetor elemento de área infinitesimal.

Aplicando o Teorema da Divergência na equação (4) e considerando uma distribuição volumétrica de massa, obtém-se a Lei de Gauss da Gravitação em seu formalismo diferencial:


\(\vec{\bigtriangledown }. \vec{g}=-4\pi G\rho_m\), (5)


em que \(\rho_m\) é a densidade da distribuição volumétrica de massa.

O sinal negativo apresentado na equação (5) demonstra que os campos gravitacionais são sempre convergentes.


Túnel no Interior de uma Esfera Maciça Dielétrica

Seja uma esfera maciça dielétrica de raio \(R\), uniformemente carregada com carga positiva \(+Q\) e com densidade volumétrica de carga constante \(\rho_q\). Essa esfera apresenta um túnel reto ao longo do eixo \(z\), partindo da superfície em direção ao seu centro \(O\) e saindo na superfície diametralmente oposta. O diâmetro do túnel é desprezível em relação ao tamanho da esfera. Considera-se, agora, que um elétron de carga \(−e\) e massa \(m_e\) seja abandonado a partir do repouso na entrada do túnel e que não haja nenhuma outra força relevante além da força eletrostática (tais como as forças gravitacional e magnética), como mostrado na FIGURA 1.


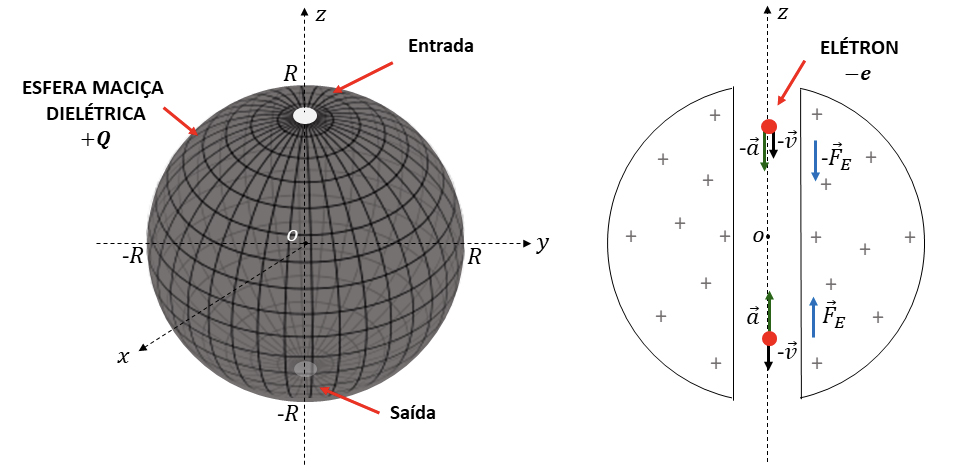
FIGURA 1. Representação esquemática de um elétron no interior de um túnel conectando os extremos de uma esfera maciça dielétrica de raio \(R\) e uniformemente carregada com carga \(+Q\), onde \(\vec{F}_E\) é a força eletrostática sobre o elétron e \(\vec{v}\) e \(\vec{a}\) são, respetivamente, sua velocidade e aceleração.

Como esse problema apresenta simetria esférica, pode-se utilizar facilmente a Lei de Gauss da Eletrostática para determinar o campo elétrico \(\vec{E}\) em um ponto que se localize a uma distância radial \(r\) do centro da esfera. Então, para qualquer ponto no interior da esfera \(( r<\)\( R)\), tem-se que:


\(\oint \vec{E}. d\vec{S}=\frac{1}{\varepsilon _0}\int \rho_q dV\)

\(E\int_{0}^{2\pi}\int_{0}^{\pi}r^{2}\sin \theta d\theta d\phi=\frac{\rho_q}{\varepsilon _0}\int_{0}^{r}\int_{0}^{2\pi}\int_{0}^{\pi}r^2 \sin \theta d\theta d\phi dr\)

\(E4\pi r^2=\frac{\rho_q}{\varepsilon _0}\frac{4\pi r^{3}}{3}\) (6)

\(E4\pi r^2=\frac{Qr^3}{\varepsilon _0R^3}\)

\(\vec{E}\left ( r \right )=\frac{Qr}{4\pi \varepsilon _0R^3}\hat{r}\).


Portanto, o campo elétrico \(\vec{E}\) no interior do túnel em função de uma distância \(z <\)\( R\) do centro \(O\) é dado por:


\(\vec{E}\left ( z \right )=\frac{Qz}{4\pi\varepsilon _0 R^3}\hat{k}\) (7)


Dessa forma, o elétron no interior do túnel fica sujeito a uma força eletrostática \(\vec{F}_E\) expressa por:


\(\vec{F}_E=\left ( -e \right )\vec{E}=-\frac{Qez}{4\pi\varepsilon _0 R^3}\hat{k}\), (8)


em que \(e=1,60\times 10^{-19}C\) é o modulo da carga do elétron.

Pode-se observar que essa força possui o mesmo formato da Lei de Hooke9 Portanto, esse resultado leva a inferir que assim como um corpo conectado a uma mola de constante elástica \(k\) e livre de forças externas executa um MHS (Movimento Harmônico Simples10) em torno de uma posição de equilíbrio devido a força elástica \(\vec{F}_e\) e (Lei de Hooke), o elétron também executa um MHS em torno do centro \(O\) do túnel devido à força eletrostática \(\vec{F}_E\) dada pela equação (8). Assim, nesse problema, fica claro que a força eletrostática se comporta como uma força restauradora..

Utilizando a Segunda Lei de Newton, é possível determinar a equação do MHS que o elétron descreve no interior do túnel:


\(\vec{F}_{res}=\frac{d\vec{p}}{dt}=m_e\vec{a}\), (9)


onde \(\vec{p}=m_e\vec{v}\) é o momento linear do elétron de massa \(m_e=9,11\times 10^{-31}\)kg, velocidade \(\vec{v}\) e aceleração \(\vec{a}\).

Substituindo a equação (8) na equação (9), obtém-se:


\(-\frac{Qez}{4\pi \varepsilon _0R^3}=m_e\frac{d^2z}{dt^2}\)

\(\frac{d^2z}{dt^2}+\frac{Qe}{4\pi \varepsilon _0m_eR^3}z=0\). (10)


Note que a equação (10) apresenta a forma típica da equação de um oscilador harmônico simples, cuja frequência angular natural \(\omega\) é dada por:


\(\omega^2=\frac{Qe}{4\pi \varepsilon _0m_eR^3}\). (11)


Então, pode-se concluir que o elétron ao ser abandonado a partir do repouso na entrada do túnel se movimentaria com velocidade crescente até o centro \(O\) da esfera e lá chegaria com velocidade máxima, isto é, energia cinética \(K\) máxima. Posteriormente, seguiria afastando-se do centro da esfera, desacelerando, até a outra extremidade do túnel, onde novamente pararia ao atingir a energia potencial elétrica \(U\) máxima. Novamente cairia em direção ao centro, oscilando dentro desse túnel em MHS. Essa é a típica situação da conservação da energia mecânica \(E_{mec}\), onde a energia potencial \(U\) se transforma em cinética \(K\) e vice-versa.

A partir da equação (11), pode-se determinar o período \(T\) e a frequência de oscilação \(f\) do elétron:


\(T=\sqrt{\frac{16\pi^3\varepsilon _0m_eR^3}{Qe}}\) (12)


e


\(f=\sqrt{\frac{Qe}{16\pi^3\varepsilon _0m_eR^3}}\). (13)


Uma possível solução da equação (10) é dada por:


\(z\left ( t \right )=R\cos\left ( \omega t \right )\). (14)


As funções velocidade \(v (t)\) e aceleração \(a (t)\) podem ser obtidas, respetivamente, por meio da derivada da primeira e segunda derivada temporal de \(z (t)\):


\(v\left ( t \right )=\frac{dz}{dt}=-R\omega \sin \left ( \omega t \right )\), (15)


e


\(a\left ( t \right )=\frac{d^2z}{dt^2}=-R\omega^2 \cos \left ( \omega t \right )\). (16)


A velocidade média \(v_{m\acute{e}d}\) desenvolvida pelo elétron no interior desse túnel é dada por:


\(v_{m\acute{e}d}=\frac{2R}{T/2}=\frac{4R}{T}\) (17)


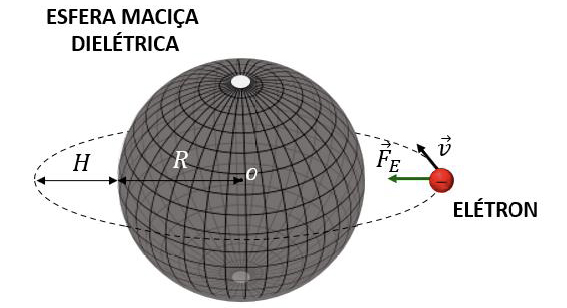
Nota-se que a equação para o período \(T\) de um elétron orbitando a mesma esfera dielétrica de raio \(R\) e uniformemente carregada com carga \(+Q\), a partir de uma distância \(H\) de sua superfície (FIGURA 2), possui o mesmo formato da equação (12). Tal resultado pode ser obtido igualando o módulo da força eletrostática \(F_E\) ao módulo da força centrípeta \(F_c\), conforme segue:


\(F_c=F_E\)

\(\frac{m_ev^2}{R+H}=\frac{Qz}{4\pi\varepsilon _0\left ( R+H \right )^{3}}\)

\(m_e\left [ \frac{2\pi\left ( R+H \right )}{T} \right ]^{2}=\frac{Qz}{4\pi\varepsilon _0\left ( R+H \right )^{2}}\) (18)

\(T=\sqrt{\frac{16\pi^3\varepsilon _0m_e\left ( R+H \right )^{3}}{Qe}}\).


FIGURA 2. Representação esquemática de um elétron orbitando uma esfera maciça dielétrica de raio \(R\) e uniformemente carregada com carga \(+Q\), a partir de uma distância \(H\) de sua superfície.


Túnel no Interior de um Astro Rochoso

Seja, agora, um túnel reto com as mesmas características apresentadas anteriormente, mas que neste caso conecte os dois extremos da superfície de um astro rochoso. Considera- se que o astro possa ser modulado como uma esfera maciça de raio \(R\), massa \(M\) e densidade volumétrica de massa constante \(\rho_m\). Seja uma partícula de massa \(m\) abandonada a partir do repouso na entrada do túnel e que a força gravitacional seja a única força relevante do problema.

Utilizando a Lei de Gauss da Gravitação pode-se obter o campo gravitacional \(\vec{g}\) no interior do túnel em relação a uma distância \(z <\)\( R\) do centro \(O\) do túnel do astro rochoso:


\(\vec{g}\left ( z \right )=-\frac{GMz}{R^3}\hat{k}\) (19)


e a força gravitacional \(\vec{F}_G\) que a partícula de massa \(m\) fica sujeita no interior do túnel é:


\(\vec{F}_G=m\vec{g}=-\frac{GMmz}{R^3}\hat{k}\). (20)


Pode-se notar que a força gravitacional \(\vec{F}_G\) também possui o mesmo formato que a Lei de Hooke9.

Portanto, a partícula massiva também executa um MHS em torno do centro \(O\) do túnel devido a força gravitacional \(\vec{F}_G\) dada pela equação (20).

Aplicando a Segunda Lei de Newton, obtém-se a equação do MHS que a partícula de massa \(m\) descreve no interior do túnel:


\(\frac{d^2z}{dt^2}+\frac{GM}{R^3}z=0\) (21)


onde a frequência angular natural \(\omega '\) é dada por:


\(\omega '^{2}=\frac{GM}{R^3}\). (22)


Através da equação (22), é possível obter o período \(T′\) e a frequência de oscilação \(f′\) da partícula massiva:


\(T'=2\pi \sqrt{\frac{R^3}{GM}}\) (23)


e


\(f'=\frac{1}{2\pi}\sqrt{\frac{GM}{R^3}}\). (24)


A solução da equação (21) admite o mesmo formato da equação (14).

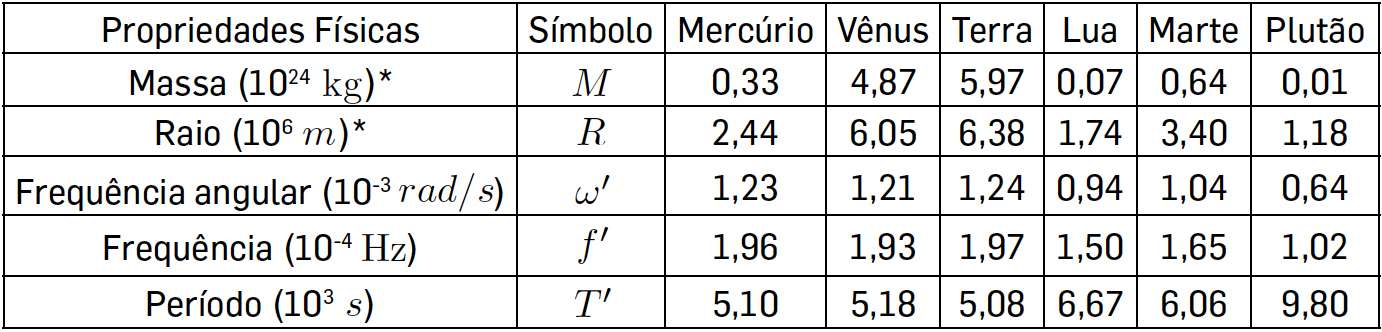
A nível de curiosidade, apresentam-se na TABELA 1 valores de frequência angular natural, frequência de oscilação e período para uma massa \(m\) movendo-se em MHS no interior de um túnel que atravessa diferentes astros rochosos.


TABELA 1. Quantidades físicas relacionadas ao MHS para uma massa \(m\) no interior de um túnel que atravessa diferentes astros rochosos.
* Obtidos de Lunar and Planetary Science. National Aeronautics and Space Administration – NASA11.

É interessante ressaltar que nesse caso, o período \(T′\) obtido pela equação (23) também possui o mesmo formato do período de uma massa \(m\) orbitando a mesma esfera maciça de raio \(R\) e massa \(M\) a partir de uma distância \(H\) de sua superfície. De forma análoga ao que foi feito anteriormente, o resultado pode ser obtido igualando o módulo da força gravitacional \(F_G\) ao módulo da força centrípeta \(F_c\):


\(F_c=F_G\)

\(\frac{mv^2}{R+H}=\frac{GMm}{\left ( R+H \right )^{2}}\)

\(\left [ \frac{2\pi\left ( R+H \right )}{T'} \right ]^{2}=\frac{GM}{R+H}\) (25)

\(\frac{4\pi^{2}}{T'^2}\left ( R+H \right )=GM\)

\(T'=2\pi \sqrt{\frac{\left ( R+H \right )^{3}}{GM}}\).


Por fim, comparam-se, a seguir, os períodos dados pelas equações (12) e (23). Para tal, considera-se que a esfera dielétrica de carga \(+Q\) da situação 1 é constituída de \(N\) prótons e a esfera maciça de massa \(M\) da situação 2 de \(N\) átomos de hidrogênio. Então:


\(\frac{T'}{T}=\frac{2\pi\sqrt{\frac{R^3}{GM}}}{\sqrt{\frac{16\pi^3\varepsilon _0m_eR^3}{Q_e}}}=2\pi\sqrt{\frac{4\pi^2Qe}{GM16\pi^3 \varepsilon _0m_e}}=\frac{\sqrt{e^2}}{Gm_H4\pi\varepsilon _0m_e}\approx 5\times 10^{19}\). (26)


onde \(m_H\) é a massa do átomo de hidrogênio

Tal resultado evidencia o fato da intensidade da força gravitacional \(\vec{F}_G\) ser muito menor que a intensidade da força eletrostática \(\vec{F}_E\), uma vez que a razão \(\frac{T'}{T}\gg 1\).

Portanto, o objetivo aqui não foi apresentar um caso realístico, mas sim corroborar as semelhanças existentes entre os campos elétrico e gravitacional. Ao utilizar exemplos de situações distintas e obter resultados extremamente similares, ratificou-se a existência da simetria entre esses dois campos. Viu-se que nos dois casos, o movimento da partícula estudada é o mesmo de um oscilador harmônico simples, sendo que no primeiro caso a força restauradora é desempenhada pela força eletrostática e no segundo caso pela força gravitacional.