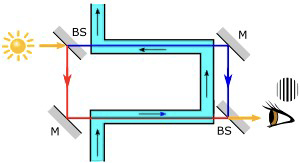
A velocidade da luz no meio interestelar (representada por \(c\)) foi estimada pela primeira vez em 1676 por O. Romer através dos atrasos nas ocultações das luas de Júpiter. Em 1848, H. Fizeau determinou aquela velocidade através de uma experiência laboratorial. Quando J. C. Maxwell deduziu (1865) que um campo eletromagnético variável no tempo se propaga no vazio como uma onda com a velocidade da luz¹, parecia evidente que se poderia medir a velocidade da Terra em relação ao meio interestelar (então designado por éter) através de uma experiência de óticaa. Para este efeito, A. Michelson e E. Morley montaram em 1887 um dispositivo de interferometria (FIGURA 1A)) esquematicamente representado na FIGURA 1B).

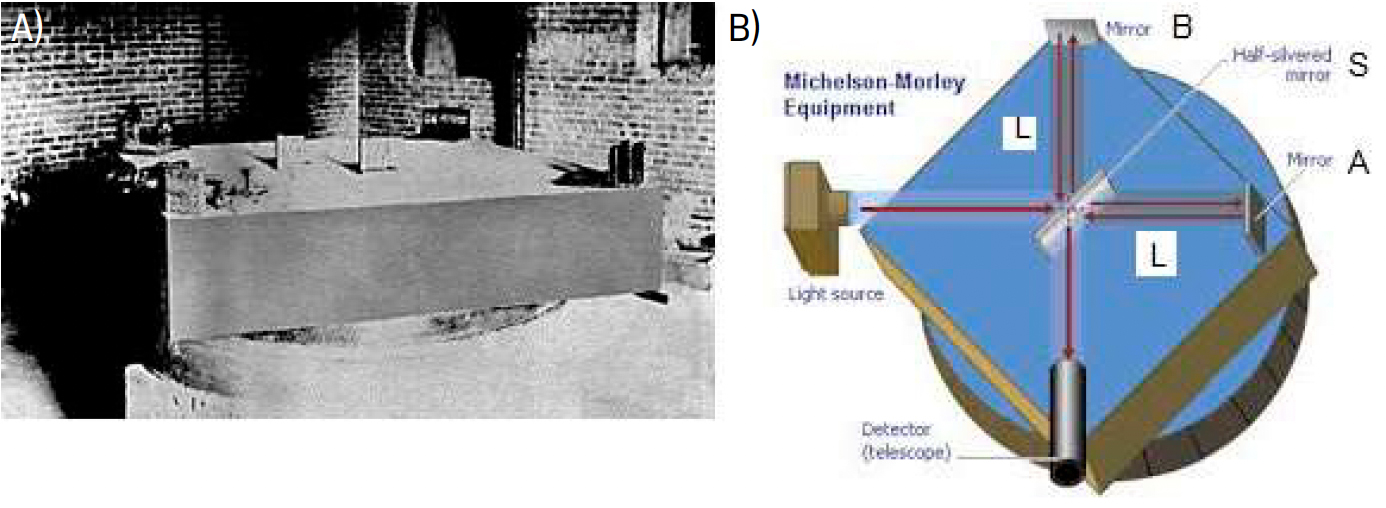
Um feixe de luz é enviado da fonte (lâmpada de sódio) até uma lâmina (S) que o divide em dois: um continua o caminho até um espelho (A) que o reflecte de volta para a lâmina e daí para o detetor; o outro reflecte na lâmina é enviado para uma direção perpendicular ao primeiro onde é refletido por outro espelho (B) e daí para o detetor. Neste é observada a sobreposição das duas ondas a qual depende dos tempos despendidos pelos raios nos seus percursos e que se resumem, afinal, aos tempos entre a saída da lâmina e o regresso à mesma (os outros percursos são comuns aos dois raios)

Aceite-se, para simplificar, que a distância (L) da lâmina aos espelhos é a mesma. Que resultado se deveria esperar? Para um observador em repouso no “éter”, a velocidade da luz é isotrópica; imagine-se que, para tal observador, a Terra se move com velocidade V no sentido SA. Então o raio que percorre este braço demora um tempo \(\frac{L}{c+V}\) para ir de S até A (porque o espelho A se afasta) e um tempo \(\frac{L}{c-V}\) de A até S (porque a lâmina S se aproxima), daqui resultando o tempo total \(t_{SA}=\frac{2L}{c}\frac{1}{1-\left ( \frac{V}{C} \right )^2}\). Para o outro percurso, o observador vê o raio seguir os lados de um triângulo isósceles do qual as posições inicial e final da lâmina são os vértices da base (FIGURA 2); um cálculo simples mostra que o tempo total para este percurso é \(t_{SB}=\frac{2L}{c}\frac{1}{1- \sqrt{1-\left ( \frac{V}{C} \right )}^2}\).

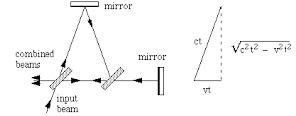
A diferença \(t_{SB}-t_{SA}\) deveria traduzir-se numa interferência² das duas ondas originando no detetor um registo de intensidade inferior à que seria obtida se os raios chegassem ao mesmo tempo (os braços do interferómetro tinham comprimento L = 11m; para a velocidade V = 3x104 m/s da Terra em torno do Sol, obtém-se \(c\left ( t_{SB}-t_{SA} \right )\) = 110nm, inferior aos 590nm do comprimento de onda da radiação emitida pelo sódio). Mas a experiência, repetida e melhorada durante mais de 20 anos, deu resultado nulo: os dois raios chegam ao mesmo tempo! Como é possível a velocidade da luz ser a mesma no “éter” e na Terra quando esta se move naquele meio?

O princípio da relatividade.

Em 1632, Galileu, na sua histórica obra Dialogo sopra I due sistemi del^a mondi, estabeleceu o primeiro princípio da relatividade: não é possível distinguir através de uma experiência mecânica, se se está em repouso ou em movimento retilíneo e uniforme. Imaginem-se dois observadores: um (R) arbitrariamente considerado em repouso e o outro (M) em movimento uniforme e retilíneo em relação ao primeiro, com a velocidade V. Segundo Galileu, qualquer experiência mecânica realizada por R terá o mesmo resultado que a mesma experiência realizada por M em idênticas condições. Deste modo, dois relógios iguais, um em repouso para R e o outro em repouso para M, batem ao mesmo ritmo para os respetivos observadores. Seja \(\left ( x,y,z \right )\) um sistema de eixos cartesianos com origem em R e o eixo \(x\) alinhado na direção do movimento de M; analogamente, seja \(\left ( x',y',z' \right )\) um sistema de eixos cartesianos com origem em M e o eixo \(x′\) sobreposto ao eixo \(x\). A relação entre as coordenadas e os tempos marcados pelos relógios para qualquer acontecimento é conhecida por transformação de Galileu:

\(t=t'\; \; \; \; \; x=x'+Vt'\; \; \; \; \; y=y'\; \; \; \; \; z=z'\) (1)

onde se aceitou, por convenção, que no instante inicial \(\left ( t=t'=0 \right )\) as duas origens coincidem e os dois relógios estão acertados. Mas a primeira equação em (1) tem um significado adicional: quando passar 1s no relógio de \(\left ( \Delta t'=1 \right )\) também passa 1s no relógio de R \(\left ( \Delta t=1 \right )\), i.e., os dois relógios permanecem sincronizados. A transformação de Galileu está na base de toda a mecânica newtoniana, mas dela decorre que se R enviar um raio de luz ao longo do eixo \(x\), i.e, \(x=ct\), então é \(x'=\left ( cV \right )t'\) pelo que M mediria a velocidade \(c − V\) para esse raio de luz, o que é manifestamente negado pela experiência de Michelson-Morley.

A teoria da relatividade restrita generaliza o princípio de Galileu, assentando em dois postulados de grande simetria:

1.º: Nenhuma experiência, seja qual for a sua natureza, permite distinguir o estado de repouso do estado de movimento uniforme e retilíneo. Os dois observadores R e M são inteiramente equivalentes na descrição de qualquer experiência. Assim, as leis da Física devem ser escritas sob uma forma que estabeleça esta equivalência (princípio da covariância), tal como em Física clássica a escrita das leis sob forma vetorial as torna independentes do referencial que se utilize.

2.º: A velocidade da luz no vazio é a mesma para os observadores R e M, sendo a maior velocidade a que se pode transmitir qualquer informação. Este postulado torna impossíveis ações instantâneas à distância e elege o campo, tal como o eletromagnético, na verdadeira realidade física onde forças são transmitidas a velocidades finitas. Como consequência, para qualquer acontecimento é necessário especificar não só onde ocorreu (definido pelas três coordenadas cartesianas) como o tempo marcado pelo relógio em repouso no ponto onde o acontecimento ocorreu. Assim, cada observador dispõe de relógios, seja qual for a sua natureza, em cada ponto do espaço que se consideram sincronizados e acertadosb. É útil considerar relógios óticaos, i.e., um raio de luz oscilando entre dois espelhos paralelos e em repouso para o observador, apresentando um período \(\frac{2l_0}{c}\) onde \(l_0\) é a distância entre os espelhos, colocando-se, porém, a questão se os relógios de R sincronizam com os relógios de M.

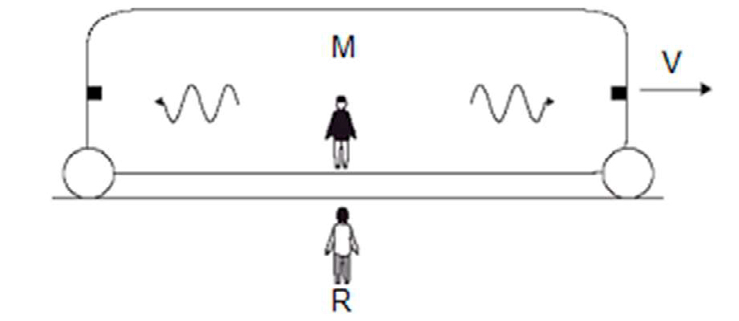
Uma primeira consequência é a relatividade da simultaneidade como se exibe na FIGURA 3. Para M, situado a meio da distância entre os dois alvos, os dois raios que emitiu no mesmo instante chegam no mesmo instante aos alvos; mas para R o raio da esquerda chega antes do raio da direita! Imagine-se agora que M orienta o seu relógio óticao de modo que o raio de luz oscila segundo o eixo \(y′\); o seu período é \(\Delta t'=\frac{2l_0}{c}\). Para R a trajetória do raio é a representada na FIGURA 2 e, para este observador, a distância entre os espelhos é também \(l_0\). De facto, suponha-se que, para R, tal distância é \(l=\alpha\left ( V \right )l_0\). O factor \(\alpha\left ( V \right )\) deve ser par, \(\alpha\left ( V \right )=\alpha\left ( -V \right )\), porque é irrelevante se o movimento se dá para a direita ou para a esquerda. Então, se M colocar aquele relógio a mover-se com velocidade \(−V\), a distância entre os espelhos deveria ser \(\alpha\left (- V \right )l_0\) para M e, portanto, seria \(\alpha\left ( V \right )\left [ \alpha\left ( -V \right )l_0 \right ]\) para R. Mas, para R, este relógio óticao está parado, pelo que \(\alpha\left ( V \right )\alpha\left (- V \right )=1\) e, portanto, \(\alpha\left ( V \right )=1\). Distâncias perpendiculares à direção do movimento são as mesmas para os dois observadores. Ora o período que R atribui a tal relógio já foi calculado na FIGURA 2:

\(\Delta t=\frac{\Delta t'}{\sqrt{1-\left ( \frac{V}{c} \right )^2}}>\Delta t'\) (2)

O relógio (qualquer relógio!) em movimento bate mais lentamente para um observador em repouso – tal é designado por dilatação do tempo. Pela simetria entre os observadores, também o relógio de R bate mais lentamente para M: não há contradição porque a única forma de comparar os relógios seria o observador M ficar em repouso com R, o que manifestamente significa que o seu movimento deixaria de ser uniforme e retilíneo. É habitual designar-se por factor de Lorentz \(\left ( \gamma \right )\) a razão daqueles períodos, i.e.:

\(\gamma\equiv \frac{1}{\sqrt{1-\left ( \frac{V}{c} \right )^2}}\) (3)

Exemplo: o muão decai, no laboratório, ao fim de \(\tau =\)2,2\(\mu\)s . Raios cósmicos produzem muões a cerca de 2Km de altitude, por colisão com moléculas. Os muões viajam à velocidade \(\frac{V}{c}=\)0,994 , obtendo-se \(\gamma \simeq \)10 . Não fosse a dilatação do tempo, os muões teriam desaparecido após \(V_{\tau }\simeq \)600m, mas por causa da dilatação os muões sobrevivem numa distância \(V\gamma \tau \simeq \)6Km, sendo detetados no solo.

O observador M roda o seu relógio óticao ficando os espelhos perpendiculares ao eixo \(x′\). O período não é alterado (se fosse, o observador saberia que estava em movimento). Qual o período para R? Se \(l\) designar a distância entre os espelhos para este observador, o período é o intervalo de tempo entre a partida do raio num espelho, sua reflexão no segundo espelho e regresso ao primeiro espelho. Este cálculo também já foi apresentado para o braço “horizontal” do interferómetro de Michelson, tendo-se encontrado \(\Delta t=\frac{2l}{c}\frac{1}{1-\left ( \frac{V}{c} \right )^2}\). Mas este período é o mesmo da eq. (2) – a relação entre os relógios de R e M não depende da orientação dos mesmos! Comparando, obtém-se o a distância entre os espelhos atribuída por R:

\(l=l_0\sqrt{1-\left ( \frac{V}{c} \right )^2}=\frac{l_0}{\gamma}\) (4)

A distância aparece mais curta para o observador que vê os espelhos em movimento, fenómeno conhecido por contração de Lorentz. Percebe-se agora melhor o resultado nulo da experiência de Michelson-Morley. Para o observador terrestre, onde a experiência foi feita, os tempos nos dois braços são iguais porque têm o mesmo comprimento e a velocidade da luz é \(c\). Para o observador no “éter”, os tempos são iguais porque o braço horizontal, paralelo à direção da velocidade da Terra, apresenta a contração de Lorentz.

A transformação de Lorentz.

Pode agora estabelecer-se a relação entre as coordenadas espaciais e temporais que R e M atribuem a um mesmo acontecimento. As distâncias perpendiculares à direção do movimento relativo são iguais, como se mostrou, pelo que \(y = y′\) e \(z = z′\). Se M atribui a distância \(x′\) ao acontecimento, a distância deste a M é \(\frac{x'}{\gamma}\) para R (pela contração de Lorentz) e situando-se M à distância \(V t\) de R, então obtém-se:

\(x=Vt+\frac{x'}{\gamma}\; \; \; \; \; \rightarrow \; \; \; \; \; x'=\gamma\left ( x-Vt \right )\) (5)

Dada a simetria entre os dois observadores, é imediato obter a relação inversa (R move-se para M com velocidade \(−V\)), tendo-se:

\(x=\gamma\left ( x'+Vt' \right )\) (6)

Eliminando \(x\) entre estas equações, obtém-se:

\(t=\gamma\left ( t'+\frac{Vx'}{c^2} \right )\) (7)

Imediatamente se deduz a relação inversa:

\(t'=\gamma\left ( t-\frac{Vx}{c^2} \right )\) (8)

Ficam assim estabelecidas as relações entre coordenadas e tempos atribuídas pelos dois observadores ao mesmo acontecimento. São conhecidas por transformações de Lorentz e reduzem- se à transformação de Galileu, eq. (1), para baixas velocidades \(\left ( V\ll c \right )\).

\(t=\gamma\left ( t'+\frac{Vx'}{c^2} \right )x=\gamma\left ( x'+Vt' \right )y=y'z=z'\) (9)

Considerando estas relações sob forma matricial, é fácil concluir que o determinante da matriz é 1. A matriz que relaciona as coordenadas e tempo de M em termos dos de R, é igual à matriz inversa da anterior e dela se obtém simplesmente trocando \(V\) por \(−V\):

\(t'=\gamma\left ( t-\frac{Vx}{c^2} \right )x'=\gamma\left ( x-Vt \right )y'=yz'=z\) (10)

Espaço-tempo.

Designa-se por espaço-tempo o lugar geométrico dos acontecimentos etiquetados pelas coordenadas \(\left ( ct,x,y,z \right )\) e que obedecem à transformação de Lorentz sob uma mudança de observador. É comum resumir aquelas coordenadas usando a notação \(\left ( x^{\mu} \right )\) com \(\mu=\)0,1,2,3 e a identificação \(x^0\equiv ct,x^1\equiv x,x^2\equiv y,x^3\equiv z\), ou, de forma condensada, \(x^{\mu}\equiv \left ( ct,\vec{r} \right )\) onde \(\vec{r}\) é o habitual vetor de posição na geometria tridimensional. Por analogia com esta geometria, define-se quadrivetor qualquer conjunto ordenado de quatro grandezas que se transformam como \(x^{\mu}\) e aquelas quatro grandezas designam-se por componentes contravariantes do respetivo quadrivetor. Adiante serão apresentados alguns exemplos.

Considerem-se dois acontecimentos no espaço-tempo, um que ocorre em \(\left ( ct_1,x_1,y_1,z_1 \right )\) e o outro em \(\left ( ct_2,x_2,y_2,z_2 \right )\). Define-se intervalo entre estes acontecimentos a grandeza:

\(s^2=c^2\left ( t_2-t_1 \right )^2-\left ( x_2-x_1 \right )^2-\left ( z_2-z_1 \right )^2=c^2\left ( t_2-t_1 \right )^2-\left | \vec{r}_2-\vec{r}_1 \right |^2\) (11)

É fácil mostrar que o intervalo é um invariante, i.e., permanece o mesmo sob uma transformação de Lorentz:

\(s^2=c^2\left ( t_2-t_1 \right )^2-\left | \vec{r}_2-\vec{r}_1 \right |^2=c^2\left ( t_{2}^{'}-t_{1}^{'} \right )^2-\left | \vec{r}_{2}^{'}-\vec{r}_{1}^{'} \right |^2\)

Para acontecimentos muito próximos no espaço-tempo obtém-se:

\(ds^2=c^2dt^2-\left | d\vec{r} \right |^2\) (12)

O intervalo desempenha um papel análogo à distância na geometria tridimensional. Mas, ao contrário desta, o intervalo pode ser positivo, nulo ou negativo. É nulo apenas para um raio de luz: a distância entre os dois acontecimentos, \(\left | \vec{r}_2-\vec{r}_1 \right |\), é exatamente igual à distância percorrida pelo raio de luz, \(c\left | t_2-t_1 \right |\) que tenha partido de \(\vec{r}_1\) no instante \(t_1\) e chegado a \(\vec{r}_2\) no instante \(t_2\). Para os outros valores do intervalo, suponha-se, para simplificar, que, para o observador R, um dos acontecimentos ocorre na origem, \(x^{\mu}=0\), e que o outro tem nulas as coordenadas \(y\) e \(z\), de modo que \(s^2=c^2t^2-x^2\). Ora:

i) Se \(s^2> 0\) existe um observador M para o qual os dois acontecimentos ocorreram no mesmo ponto do espaço em tempos diferentes. Com efeito, usando a transformação de Lorentz deduz-se a velocidade de M:

\(0<\)\(s^2=c^2t^2-x^2=c^2t'^2=\gamma^2c^2\left ( t-\frac{xV}{c^2} \right )^2\rightarrow V=\frac{x}{t}\)

Os dois acontecimentos dizem-se temporalmente separados, podendo um deles ser a causa do outro. Por exemplo, uma explosão no Sol (tomado como origem) provocou intensa radiação UV, verificando-se que um satélite, a 300 s-luz do Sol ficou danificado 500s após a explosão: \(s^2 = 500^2− 300^2 = 400^2\): os dois acontecimentos são percebidos por um observador M (mesmo ponto!) movendo-se com a velocidade \(V=\frac{3c}{5}\) (em relação ao Sol) e separados por 400s (no relógio desse observador).

ii) Se \(s^2<\) \(0\) existe um observador M para o qual os dois acontecimentos ocorreram no mesmo instante em pontos distintos do espaço. Com efeito, usando a transformação de Lorentz deduz-se a velocidade de M:

\(0>s^2=c^2t^2-x^2=-x'^2=-\gamma^2\left ( x-Vt \right )^2\rightarrow V=\frac{c^2t}{x}\)

Os dois acontecimentos dizem-se espacialmente separados, não podendo um deles ser a causa do outro. Retomando o exemplo anterior, verificou-se uma avaria num satélite a 500 s-luz do Sol, 300s após a explosão solar: \(s^2 = 300^2− 500^2 = −400^2\). Os dois acontecimentos são percebidos pelo mesmo observador M no mesmo instante (relógio de M), separados por uma distância de 400 s-luz.

A FIGURA 4 é uma representação gráfica do espaço-tempo e de vários resultados já obtidos. As linhas vermelhas são trajetórias de raios de luz passando por M e designam-se por cone de luz^d: bissetam os eixos \(ct\) e \(x\). O interior da folha superior do cone de luz é o futuro absoluto de M; o interior da folha inferior é o passado absoluto de M. Qualquer linha que represente o movimento de um observador ou de uma partícula é designada por linha de mundo da respetiva entidade: a linha vertical \(x = 0\) é a linha de mundo de R, e a reta azul linha de mundo de M — é o seu eixo \(ct′\), com declive \(\frac{c}{V}>1\). Este resultado é genérico: para qualquer linha representando o movimento de uma partícula (a verde em \(a\)), o declive em cada ponto é \(\frac{d\left ( ct \right )}{dx}=\frac{c}{v\left ( t \right )}>1\).

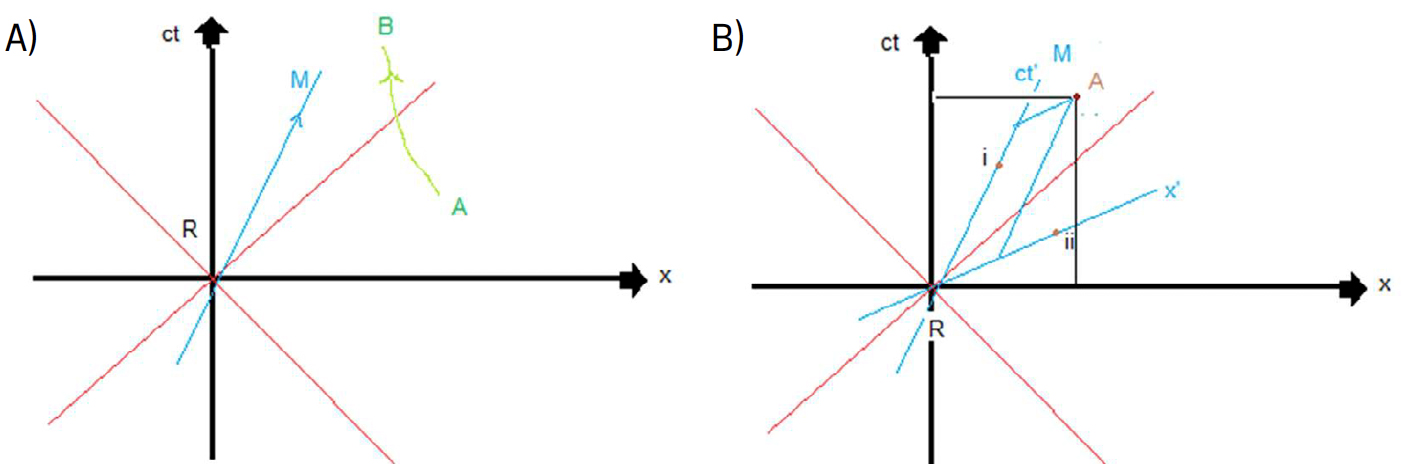
Na FIGURA 4B) são representados os eixos dos dois observadores: como os raios de luz bissetam os eixos \(ct\) e \(x\), então deverão bissetar os eixos \(ct′\) e \(x′\), o que permite desenhar este último eixo. Os pontos i e ii representam os acontecimentos referidos nos exemplos anteriores. Para um acontecimento genérico A, as suas coordenadas, para R, obtêm-se tirando paralelas aos eixos \(ct\) e \(x\) até os intersetar, e, para M, de modo análogo, tirando paralelas aos eixos \(ct′\) e \(x′\) até os intersetar. Note-se, porém, que as unidades são diferentes: \(\Delta t′ = 1\) corresponde a \(\Delta t =\gamma\) (dilatação do tempo) e \(\Delta x′ =\gamma^{-1}\) corresponde a \(\Delta x = 1\) (contração de Lorentz).

Quadrivetores

Para uma partícula em movimento, a velocidade, para R, é o vetor tridimensional \(\left ( \frac{dx}{dt},\frac{dy}{dt},\frac{dz}{dt} \right )\) e, para M, é o vetor tridimensional \(\left ( \frac{dx'}{dt'},\frac{dy'}{dt'},\frac{dz'}{dt'} \right )\). Usando a transformação de Lorentz, eq. (9), obtém-se^e:

\(v_x=\frac{v'_{x'}+V}{1+\frac{Vv_{x'}'}{c^2}}\; \; \; \; \; v_y=\frac{1}{\gamma}\frac{v'_{y'}}{1+\frac{Vv_{x'}'}{c^2}}\; \; \; \; \; v_z=\frac{1}{\gamma}\frac{v'_{z'}}{1+\frac{Vv_{x'}'}{c^2}}\) (13)

Facilmente se deduz a relação:

\(1-\frac{\vec{v}^2}{c^2}=\frac{1}{\gamma^2}\frac{1-\frac{\vec{v}^2}{c^2}}{\left ( 1+\frac{Vv'_{v'}}{c^2} \right )^2}\) (14)

verificando o acordo com o segundo postulado \(\left ( \left | \vec{v} \right |=c\leftrightarrow \left | \vec{v}' \right |=C \right )\). Se uma fonte de luz (por exemplo, uma estrela), em repouso para R, emitir um feixe de luz fazendo um ângulo \(\theta\) com a direção do eixo \(x\), i.e., o feixe tem a velocidade \(-c\left ( \cos\theta,\textrm{sen}\theta \right )\), o observador M (por exemplo, astrónomo) recebe o raio sob um ângulo \(\theta '\) que se obtém da primeira das equações inversas de (13), vindo:

\(\cos\theta'=\frac{\cos\theta+\frac{V}{c}}{1+\frac{V}{c}\cos\theta}\) (15)

Não só existe um erro de paralaxe \(\left ( \theta\neq\theta' \right )\) como, para altas velocidades de M (ou da fonte em relação a M) o feixe aparece concentrado sob o mesmo ângulo, aumentando a intensidade caso M se aproxime da fonte \(\left ( V>0\rightarrow \theta'\simeq 0 \right )\) ou diminuindo a intensidade caso M se afaste da fonte \(\left ( V<0\rightarrow \theta'\simeq \pi \right )\). Este fenómeno, conhecido por focagem relativista^f, tem grande importância em Cosmologia.

Usando a eq. (14) , reescrevem-se as eqs. (13) sob a forma:

\(\frac{1}{\sqrt{1-\frac{\vec{v}^2}{c^2}}}=\gamma\frac{1+\frac{Vv_{x'}^{'}}{c^2}}{\sqrt{1-\frac{\vec{v}^2}{c^2}}};\frac{v_x}{\sqrt{1-\frac{\vec{v}^2}{c^2}}}=\gamma\frac{v_{x'}^{'}+V}{\sqrt{1-\frac{\vec{v}^2}{c^2}}};\frac{v_y}{\sqrt{1-\frac{\vec{v}^2}{c^2}}}=\frac{v_{y'}^{'}}{\sqrt{1-\frac{\vec{v}^2}{c^2}}};\frac{v_z}{\sqrt{1-\frac{\vec{v}^2}{c^2}}}=\frac{v_{z'}^{'}}{\sqrt{1-\frac{\vec{v}^2}{c^2}}}\) (16)

Comparando com as eqs. (9), conclui-se que estas quatro grandezas se transformam como \(\left ( ct,x,y,z \right )\), o que leva à identificação do quadrivetor velocidade:

\(v^{\mu}\equiv \frac{1}{\sqrt{1-\frac{\vec{v}^2}{c^2}}}\left ( c,v_x,v_y,v_z \right )=\frac{1}{\sqrt{1-\frac{\vec{v}^2}{c^2}}}\left ( c,\vec{v} \right )\) (17)

Este resultado pode ser obtido mais facilmente notando que para o movimento de uma partícula com velocidade \(\vec{v}\), a eq. (12) dá \(ds=cdt\sqrt{1-\left ( \frac{\vec{v}}{c} \right )^2}\), sendo imediato verificar que \(v^{\mu}=c\frac{dx^{\mu}}{ds}\), o que mostra claramente ser um quadrivetor porque \(ds\) é invariante.

Tal como se definiu o intervalo a partir das componentes de \(x^{\mu}\), também se define o quadrado deste quadrivetor pelo mesmo critério, obtendo-se um invariante:

\(v^2=\left ( v^0 \right )^2-\left ( v^1 \right )^2-\left ( v^2 \right )^2-\left ( v^3 \right )^2=\left ( v^0 \right )^2-\vec{v}^2=\frac{1}{1-\frac{\vec{v}^2}{c^2}}\left ( c^2-\vec{v}^2 \right )=c^2\)

A massa \(m\) de uma partícula é um invariante: é a massa da partícula em repouso para o observador. Então \(p^{\mu}\equiv mv^{\mu}\) é um quadrivetor. Qual o seu significado? As suas componentes espaciais definem:

\(\vec{p}=\frac{m\vec{v}}{\sqrt{1-\frac{\vec{v}^2}{c^2}}}\) (18)

Esta grandeza reduz-se à quantidade de movimento da mecânica newtoniana para baixas velocidades. É, então, identificada com a quantidade de movimento relativista da partícula. Ora, pela lei fundamental da dinâmica, quando à partícula é aplicada uma força \(\vec{F}\), tem-se:

\(\vec{F}=\frac{d\vec{p}}{dt}\) (19)

A potência desta força escreve-se:

\(P=\vec{F}\cdot\vec{v}=\vec{v}\cdot\left ( \frac{d}{dt}\frac{m\vec{v}}{\sqrt{1-\frac{\vec{v}^2}{c^2}}} \right )=\frac{d}{dt}\left ( \frac{mc^2}{\sqrt{1-\frac{\vec{v}^2}{c^2}}} \right )\)

Ora, a potência de uma força é igual ao aumento, na unidade de tempo, da energia da partícula, o que leva à identificação desta grandeza:

\(E=\frac{mc^2}{\sqrt{1-\frac{\vec{v}^2}{c^2}}}\rightarrow mc^2+\frac{1}{2}m\vec{v}^2+\cdots\) (20)

A última expressão acima, obtida para baixas velocidades, mostra que, neste limite, o aumento da energia é o aumento da energia cinética newtoniana. Mas também mostra que mesmo em repouso há uma energia \(mc^2\) associada à massa da partícula, a qual desempenha um papel fundamental em reações nucleares e na física de altas energias de que alguns exemplos serão apresentados adiante.

Estes resultados mostram que o quadrivetor \(p^{\mu}=mv^{\mu}\) tem componentes:

\(p^{\mu}=\left ( \frac{E}{c},\vec{p} \right )\) (21)

É o quadrivetor energia-momento da partícula. O seu quadrado é um invariante fácil de obter:

\(p^2=\left ( \frac{E}{c} \right )^2-\vec{p}^2=\left ( mc \right )^2\) (22)

Deste modo, a energia da partícula também se pode escrever:

\(E=\sqrt{\left ( mc^2 \right )+\left ( c\vec{p} \right )^2}\) (23)

A eq. (18) mostra que partículas que viajam à velocidade da luz, por exemplo, fótão, têm necessariamente \(m = 0\), pelo que em tais casos é \(E=c\left | \vec{p} \right |\), sendo \(\vec{p}\) designado por momento linear da partícula. O fótão é o quantum da onda eletromagnética: se esta tiver frequência angular \(\omega\) e vetor de onda \(\vec{k}\), o fótão apresenta energia \(E=\frac{h\omega}{2\pi}\)  e momento linear \(\vec{p}=\frac{h\vec{k}}{2\pi}\), onde \(h\) é a constante de Planck. Pelo anterior, é nulo o quadrado do quadrivetor momento- -energia do fótão, obtendo-se simplesmente \(\left ( \frac{\omega}{c} \right )^2=\vec{k}^2\), a relação de dispersão das ondas eletromagnéticas para o vazio.

A fase de uma onda, seja qual for a sua natureza, é um invariante de Lorentz. Na experiência de Michelson-Morley as duas ondas separadas pela lâmina chegam em fase à lâmina para os dois observadores. Mais geralmente, os nodos de uma onda estacionária devem ser nodos para todos os observadores. Considere-se uma onda plana e monocromática: a sua fase é \(\vec{k}\cdot\vec{r}-\omega t\) e a invariância significa que \(\vec{k}\cdot\vec{r}-\omega t=\vec{k}'\cdot\vec{r}'-\omega't'\). Usando a transformação de Lorentz da eq. (10), facilmente se obtém a relação entre os vetores de onda e frequências para os dois observadores:

\(\omega=\gamma\left ( \omega'+k_{x'}^{'}V \right )k_x=\gamma\left ( k_{x'}^{'}+\frac{\omega'V}{c^2} \right )k_y=k_{y'}^{'}k_z=k_{z'}^{'}\) (24)

Comparando com a eq. (9), conclui-se que \(k^{\mu}\equiv \left ( \frac{\omega}{c},\vec{k} \right )\) é um quadrivetor. O seu quadrado, \(\left ( \frac{\omega}{c} \right )-\vec{k}^2\), é um invariante de Lorentz, nulo para ondas eletromagnéticas no vazio.

Exemplos.

1.º: A FIGURA 5 representa uma experiência ideal: um corpo de massa m, em repouso para o observador M, absorve dois fótões de frequência \(\nu \equiv \frac{\omega}{2\pi}\)  incidindo em sentidos opostos, pelo que o corpo aumenta a sua energia em \(\Delta E_0=2h\nu\), permanecendo em repouso porque são iguais e opostos os momentos dos fótões. Para o observador R, o corpo move-se para a direita com velocidade \(V\) e os fótões tem frequências diferentes. Usando as eqs. (24), o fótão da direita tem frequência \(\gamma\nu\left ( 1-\frac{V}{c} \right )\) e o fótão da esquerda tem frequência \(\gamma\nu\left ( 1+\frac{V}{c} \right )\). Então, para o observador R, o corpo aumentou a energia em \(\Delta E=2\gamma h\nu=\gamma\Delta E_0\) e o momento em \(\Delta P=2\gamma h\nu\frac{V}{c^2}\). Mas o corpo permanece com a mesma velocidade \(V\), pelo que o aumento do seu momento tem de ser atribuído a um aumento de massa: \(\Delta P=\Delta mV\), obtendo-se \(\Delta m=\frac{\Delta E}{c^2}\).

2.º: Em 1851, Fizeau realizou a experiência esquematizada na FIGURA 6: luz é enviada através de dois tubos percorridos por água em sentidos diferentes. As duas ondas eletromagnéticas sobrepõem-se no detetor onde se regista a intensidade. Considere-se o eixo \(x\) paralelo à velocidade \(V\ll c\) da água.

O índice de refração, \(\eta\), é definido para um meio óticao em repouso, i.e., a velocidade da luz na água é \(\frac{c}{\eta}\) para o observador M movendo-se com a água. Mas para o observador R, a velocidade da luz obtém-se das duas primeiras equações em (24), deduzindo-se a fórmula que Fizeau ajustara aos resultados da experiência:

\(v_f=\frac{\omega}{k}=\frac{v_{f}^{'}+V}{1+\frac{Vv_{f}^{'}}{c^2}}=\frac{\frac{c}{\eta}+V}{1+\frac{V}{\eta c}}\simeq \frac{c}{\eta}+V\left ( 1-\frac{1}{\eta^2} \right )\)

Há, pois, uma diferença de velocidades da luz na água entre o tubo inferior \(\left ( V>0 \right )\) e o superior \(\left ( V<0 \right )\) originando uma interferência detectável e que confirmou a fórmula anterior. Note-se que o factor \(\eta^2\) resulta da adição relativista de velocidade e estaria ausente se se empregasse a lei de adição de Galileu.

3.º: Na explosão da supernova SN1987A, situada na Nuvem de Magalhães a \(ct_0=1,68\times 10^4\) anos-luz da Terra, foram emitidos neutrinos, 12 dos quais detetados em laboratório num intervalo \(\delta t =\)3,2s com energiasg centradas em \(E_0 =\)12MeV e largura \(\delta E =\)4MeV.

Admitindo que a emissão foi instantânea, é possível estimar a massa m do neutrino: se a massa fosse nula, viajariam à velocidade da luz e teriam chegado ao mesmo tempo! O tempo de viagem dos neutrinos é \(t=\frac{ct_0}{v}\), onde \(v\) é a velocidade dos neutrinos. Eliminando a velocidade usando a eq. (20), obtém-se \(\left ( \frac{mc^2}{E} \right )=1-\left ( \frac{t_0}{t} \right )\). A dispersão na energia e nos tempos de chegada estão relacionados; diferenciando esta expressão, obtém-se:

\(\left ( \frac{mc^2}{E_0} \right )^2\frac{\delta E}{E_0}=\frac{\delta t}{t_0}\rightarrow \frac{mc^2}{E_0}\simeq 0,6\times 10^{-6}\rightarrow mc^2\approx 7eV\)

4.º: No efeito Compton, um fótão \(\gamma\) colide com um electrão em repouso (massa \(m_e\)) sendo desviado de \(\theta\) da direção original e diminuindo a sua energia (FIGURA 7).

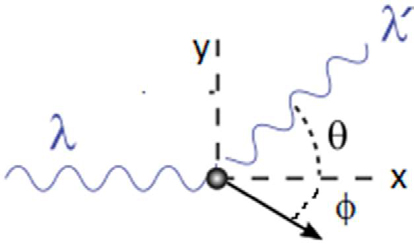
Designando por \(p\) e \(p′\) os momentos lineares do fótão, respetivamente antes e depois da colisão; por \(p_{e}^{'}\) e \(E_{e}^{'}\) o momento linear e energia do electrão após a colisão, as leis de conservação de energia e momento dão:

\(p=p'\cos\theta+p_{e}^{'}\cos\phi\)

\(0=p'\textrm{sen}\theta-p_{e}^{'}\textrm{sen}\phi\)

\(cp+m_ec^2=cp'+E_{e}^{'}\)

Eliminando o ângulo \(\phi\) nas primeiras duas equações fica:

\(\left ( p-p'\cos\theta \right )^2+\left ( p'\textrm{sen}\theta \right )^2=p_{e}^{'2}\)

A terceira equação reescreve-se:

\(\left ( p-p'+m_ec \right )^2=\left ( \frac{E_{e}^{'}}{c} \right )^2=p_{e}^{'2}+\left ( mc \right )^2\)

onde foi usada a eq. (23) para obter o último termo. As duas últimas equações dão:

\(\frac{1}{p'}-\frac{1}{p}=\frac{1}{mc}\left ( 1-\cos\theta \right )\)

Para fótões já foi encontrada atrás a relação entre o momento linear e o vetor de onda: \(p=\frac{hk}{2\pi}=\frac{h}{\lambda }\), onde \(\lambda\) é o comprimento de onda da radiação. Assim o resultado anterior escreve- se:

\(\lambda'-\lambda=\lambda_c\left ( 1-\cos\theta \right )\) (25)

onde \(\lambda_c=\frac{h}{m_ec}\simeq 2,4\times 10^{-12}\)m é o comprimento de Compton. O efeito Compton, observado e interpretado em 1923 como uma colisão inelástica fótão-electrão, foi decisivo na aceitação do conceito de quantum de luz apresentado por Einstein em 1905.

5.º: As massas das partículas elementares são habitualmente expressas em \(MeV/c^2\), uma unidade que corresponde a \(1,782\times 10^{-30}\)Kg . A tabela mostra as massas de algumas partículas:

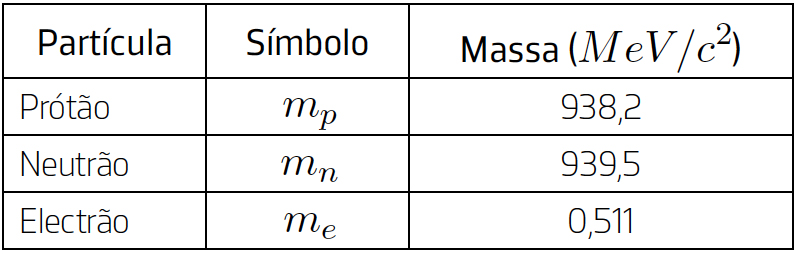
O hidrogénio atómico \(\left ( H_{1}^{1} \right )\), no estado fundamental, é constituído por um prótão e um electrão num estado ligado com a energia \(U_e = 13,6eV\) (energia que se tem de dar para colocar electrão e prótão infinitamente afastados e em repouso). Assim, a massa do átomo de hidrogénio é:

\(M\left ( H_{1}^{1} \right )=m_p+m_e-\frac{U_e}{c^2}=938,711MeV/c^2\)

Vê-se que a energia de ligação pode ser ignorada face à contribuição das massas das partículas. A unidade de massa atómica, também conhecida por Dalton (Da) é definida como \(\frac{1}{12}\) massa do \(C_{6}^{12}\) em repouso e no estado fundamental. A massa do átomo, obtida por espectroscopia de massas, é:

\(M\left ( C_{6}^{12} \right )=1, 99264687992...\times^{-26}\)Kg\(\simeq 118,8\times 10^{2}MeV/c^2\)

Assim,

\(1Da=\frac{1}{12}M\left ( C_{6}^{12} \right )=931,7MeV/c^2\)

pelo que:

\(M\left ( H_{1}^{1} \right )=1,007Da\)

O átomo de \(\left ( C_{6}^{12} \right )\) é constituído por um núcleo e 6 electrões na configuração \(1s^22s^22p^2\). A energia de ligação electrónica (a energia necessária para afastar para distâncias infinitas todos os electrões entre si e com o núcleo) pode ser estimada usando o modelo de Bohr, obtendo-se \(U_e = 40_eV\). A massa do átomo pode então escrever-se:

\(M\left ( C_{6}^{12} \right )=M\left ( 12,6 \right )+6m_e-U_e/c^2\)

onde \(M\left ( 12,6 \right )\) é a massa do núcleo. Vê-se, de novo, que a energia de ligação electrónica pode ser ignorada, obtendo-se:

\(M\left ( 12,6 \right )\simeq M\left ( C_{6}^{12} \right )-6m_e=\left ( 111,8\times 10^2-3,7 \right )MeV/c^2\)

Quer isto dizer que a massa do átomo é praticamente a massa do seu núcleo. O núcleo é formado por 6 prótões e 6 neutrões num estado ligado. Designando por \(\Delta\left ( 12,6 \right )\) a energia de ligação do núcleo, i.e., a energia que tem de ser dada para afastar para distâncias infinitas prótões e neutrões ficando em repouso, então a massa do núcleo escreve-se:

\(M\left ( 12,6 \right )=6m_p+6m_n-\frac{\Delta\left ( 12,6 \right )}{c^2}\rightarrow \Delta\left ( 12,6 \right )\simeq 86,2MeV\)

A energia de ligação nuclear representa menos de 1% da massa do núcleo. A energia de ligação nuclear por nucleão, para o \(C_{6}^{12}\), é então \(\frac{\Delta\left ( 12,6 \right )}{12}\simeq 7,2MeV\). Contudo, esta energia depende do núcleo considerado, como se mostra na FIGURA 8: cresce até ao \(\textrm{Fe}_{26}^{54}\) e diminui ligeiramente a partir daí. Adiante será retomado este tema.

Considere-se agora um átomo com número de massa A (número de neutrões e prótões no núcleo) e número atómico Z (número de electrões ou de prótões). A massa do núcleo é, então:

\(M\left ( A,Z \right )=Zm_p+\left ( A-Z \right )m_n-\frac{\Delta\left ( A,Z \right )}{c^2}\)

A FIGURA 8 mostra que \(\Delta\left ( A,Z \right )<\)\(10\times AMeV\), bem inferior às contribuições das massas dos nucleões. Ignorando a energia de ligação nuclear, a massa do núcleo fica:

\(M\left ( A,Z \right )\simeq \left [ 938,2Z+\left ( A-Z \right )939,5 \right ]MeV/c^2=\)

\(=\left [ 1,007Z+1,008\left ( A-Z \right ) \right ]Da\simeq ADa\)

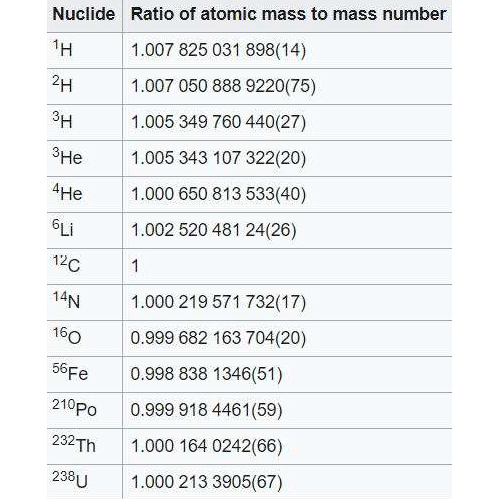
onde se usou a tabela e se converteu o valor final em daltons. Como a massa do núcleo é praticamente a massa do átomo, conclui-se que a massa do átomo expressa em daltons é praticamente o seu número de massa. A maior correção a este resultado vem da energia de ligação nuclear. A FIGURA 9 mostra o excelente acordo desta aproximação.

A fotodesintegração do deuterão tem um limiar (energia mínima do fótão) que pode deduzir-se a partir da FIGURA 9 aplicada à reação \(H_{1}^{2}+\gamma\rightarrow p+n\), obtendo-se \(\frac{E_{\gamma}}{c^2}=m_p+m_n-M\left ( H_{1}^{2} \right )\), i.e., \(E_{\gamma}=2,2MeV\) — é a energia de ligação nuclear do deuterão (ver FIGURA 8).

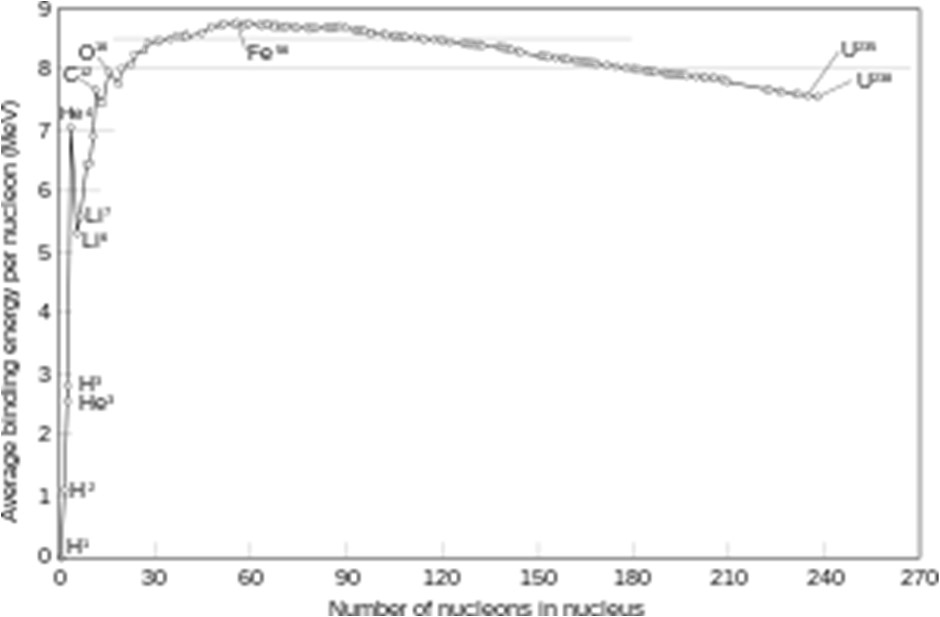
Voltando à FIGURA 8 percebe-se que o \(\textrm{Fe}_{26}^{54}\) separa dois regimes. À sua esquerda (menor Z) há um ganho de energia por fusão de núcleos: é o que se passa em estrelas que assim tentam evitar o colapso gravitacional. O ganho de energia manifesta-se na emissão de fótões \(\gamma\) e neutrinos, mas é sobretudo a pressão da radiação \(\gamma\) que evita o colapso. O processo começa com a fusão do hidrogénio, \(H_{1}^{1}+H_{1}^{1}\rightarrow H_{1}^{2}+e^++\nu\), formando-se deutério e libertando um positrão e um neutrino; depois, a fusão do deutério originando hélio; do hélio para carbono, etc.. O processo pode terminar numa destas reações conforme a massa da estrela. Mas, para estrelas de grande massa (10 ou mais vezes a massa do Sol), a fusão continua até à formação do ferro porque, a partir daí, perde-se energia por fusão. Atingido o ferro a estrela colapsa originando uma estrela de neutrões ou um buraco negro, dependendo da sua massa.

Na núcleo-síntese primordial segue-se um processo semelhante. As enormes temperaturas registadas logo após a aniquilação de matéria com antimatéria, com geração de intensa radiação, não permitem a formação estável de núcleos. A expansão do Universo arrefece-o e o primeiro núcleo composto, o deuterão, só se torna estável quando a temperatura da radiação for inferior a \(2, 2MeV\), i.e., \(T <\) \(242 \times 10^8K\).

À direita do ferro, há ganhos de energia se se diminuir o número de nucleões por emissão de neutrões ou por fissão nuclear, por exemplo, \(U_{92}^{235}\).

Estas interessantes questões sugerem tópicos para outras publicações.

A teoria da relatividade restrita não altera as equações de Maxwell³ — apenas as reescreve sob forma covariante, i.e., invocando quadrivetores e tensores definidos no espaço de Minkowski, o que, evidentemente, torna mais fácil relacionar grandezas relativas ao campo eletromagnético medidas por observadores em movimento relativo.

Os campos das forças fortes, como as nucleares, ou fracas (responsáveis pela geração de neutrinos) foram formalizados já dentro dos postulados da relatividade.

O campo gravítico só encontrou a sua formulação relativista em 1915 (Einstein), originando uma ainda mais profunda revisão dos conceitos de tempo e espaço. É um assunto muito interessante, mas que aqui não será desenvolvido.

Notas

Os dois sistemas do mundo eram os de Ptolomeu e de Copérnico.

^b O acerto de relógios não é crucial. O relógio num ponto P e outro num ponto Q estarão acertados se um raio de luz enviado de P no instante \(t_p\),marcado no relógio em P, for recebido num outro ponto Q no instante \(t_Q\), marcado no relógio em Q, tal que \(t_Q=t_p+\frac{d}{c}\) onde d é a distância entre os dois pontos.

^c Deve notar-se que 0,1,2,3 são índices e não potências.

^d A equação \(s^2=c^2t^2-x^2-y^2=0\) define um cone de duas folhas com vértice na origem.

^e As relações inversas obtêm-se trocando as variáveis com e sem plica e \(V\rightarrow -V\).

^f “Relativistic beaming”.

g \(1MeV=10^6eV;1eV\); 1eV é a energia adquirida por um electrão acelerado por uma diferença de potencial de \(1V\) – é numericamente igual à carga do electrão positivo: \(1eV=1,6022\times 10^{-19}\) e iguala a energia térmica, \(kT\) (\(k\) é a constante de Boltzmann) para \(T = 11.604K\).

 

Livros relacionados disponíveis na Loja Casa das Ciências:

1. Cadernos de Ciência – formato pdf – Relatividade Restrita

O objetivo deste pequeno Caderno de Ciência, publicado pela Casa das Ciências, é o de divulgar de uma forma simples e acessível a teoria da Relatividade Restrita, criada por Albert Einstein em 1905. É um teoria que desafia a nossa intuição, fortemente enraizada na tradição Newtoniana. No entanto, se o leitor estiver disposto a embarcar nesta fascinante viagem intelectual, com alguma matemática simples, ajuda visual e sobretudo com mente aberta, estou convicto que, no final, sairá fortemente compensado e até completamente convencido da veracidade desta criação genial de Einstein.

Este caderno contem cerca de 20 animações que ilustram o texto, ajudando a ganhar intuição sobre os conceitos expostos. As animações estão feitas em Geogebra.