Nos casos mais simples, que são também os mais vulgares, a onda, seja qual for a sua natureza, exibe, em cada ponto, uma vibração harmónica da grandeza que se propaga: designa-se por monocromática. A amplitude observada nesse ponto num dado instante, irá aparecer, um período \(T\) de vibração depois, num outro ponto – a distância entre esses pontos é o comprimento de onda (\(\lambda\)) e o seu inverso é o número de onda, i.e., o número de amplitudes na unidade de comprimento. É porém, mais comum usar-se o vector de onda (\(k\)) que indica a direcção e sentido de propagação e cuja grandeza é o número de onda multiplicado por \(2\pi\). Num dado instante, o lugar geométrico dos pontos com a mesma amplitude ou, mais geralmente, com a mesma fase, pode ser uma superfície plana, cilíndrica, esférica, etc., o que leva a classificar a onda com as mesmas designações. A propagação das amplitudes é, afinal, a propagação destes lugares geométricos: a sua velocidade é a velocidade de fase. Ora, num período de vibração (\(T\)), a amplitude repete-se no mesmo ponto, mas aquela inicialmente observada vai aparecer, \(T\) segundos depois, à distância de um comprimento de onda, pelo que a velocidade de fase é simplesmente \(\frac{\lambda}{T}\), ou, de forma equivalente, \(\frac{\omega }{k}\), onde \(\omega\) é a frequência angular¹.

A grandeza física experimentando um fenómeno ondulatório pode ser um escalar, como nas ondas de pressão ou densidade num fluido; um vector, como nas ondas electromagnéticas; ou, mais geralmente, um tensor², como nas ondas de deformação em sólidos ou as ondas gravitacionais da Relatividade Geral. Mas também pode ser algo mais abstracto, como a função de onda da Mecânica Quântica, uma função complexa do tempo e do espaço.

A natureza do meio onde se propaga a onda determina uma relação entre a frequência angular \(\omega\) e o vector de onda \(k\) - é a relação de dispersão naquele meio. Quando esta relação é linear, diz-se que não há dispersão, como acontece com as ondas electromagnéticas no vazio ou com as ondas de som no ar. Em tal caso, um sinal (i.e., uma sobreposição de ondas monocromáticas) emitido é exactamente o sinal recebido porque todas as ondas têm a mesma velocidade de fase. Mas este não é o caso geral: se a relação de dispersão é não linear, as ondas do sinal propagam-se com diferentes velocidades, alterando a forma do sinal mesmo que não haja atenuação das amplitudes. É o que se passa com a luz ao atravessar vidro ou a propagar-se na água. Adicionalmente, pode existir atenuação, diferente, em geral, para as várias ondas, se o meio onde se propaga a onda for dissipativo: no mar, o vermelho e o amarelo são mais absorvidos que o azul.

Seja qual for a sua natureza, as ondas reflectem-se ou refractam-se na superfície que separa dois meios diferentes. E difractam-se na superfície de um objecto imerso no meio ou quando obrigadas a passar por uma esquina ou por uma fenda. A difracção é a característica fundamental de uma onda, um fenómeno que depende crucialmente do comprimento de onda e que subjaz o conceito de poder separador de aparelhos ópticos, do microscópio ao telescópio.

Finalmente, uma onda confinada a um domínio finito do espaço, só pode apresentar uma selecção de comprimentos de onda, determinada pelas condições fronteira, i.e., pelas condições que as vibrações têm que satisfazer na superfície que limita o domínio – é uma onda estacionária³.

No que se segue só serão consideradas ondas planas e monocromáticas e embora se estude um caso particular, os conceitos e métodos apresentados são muito gerais, aplicando-se, praticamente, a todos os fenómenos ondulatórios.

Retome-se, aqui, a eq. (13) da Ref. 1 e que descreve o campo de deslocamentos unidimensionais \(u(x,t)\) de um meio elástico (fio metálico, barra prismática, etc.):

\(\rho \frac{\partial ^{2}u(x,t)}{\partial t^{2}}=E\frac{\partial ^{2}u(x,t)}{\partial x^{2}}\)(1)

onde \(\rho\) é a massa específica e \(E\) o módulo de Young. Este campo surgiu como limite no contínuo de uma cadeia de osciladores e descreve deslocamentos na mesma direcção da cadeia, i.e., ondas longitudinais. Na Ref. 3, a mesma cadeia vibra perpendicularmente à direcção de propagação da onda, designando-se esta, então, por transversal. Definindo \(c_{s}\equiv \sqrt{\frac{E}{\rho }} \), mostrar-se-á, a seguir, que esta grandeza é a velocidade de propagação das ondas longitudinais. Com efeito, a solução geral da eq. (1) é:

\(u(x,t)=F(x-c_{s}t)+G(x+c_{s}t)\)(2)

Considerar que a eq. (1) se pode escrever na forma \(\left ( c_{s}\frac{\partial }{\partial x}+\frac{\partial }{\partial t} \right )\left ( c_{s}\frac{\partial }{\partial x}-\frac{\partial }{\partial t} \right )u=0\), verificando-se facilmente que \(\left ( c_{s}\frac{\partial }{\partial x}+\frac{\partial }{\partial t} \right )F\left ( x-c_{s}t \right )=0\) e \(\left ( c_{s}\frac{\partial }{\partial x}-\frac{\partial }{\partial t} \right )G\left ( x+c_{s}t \right )=0\)

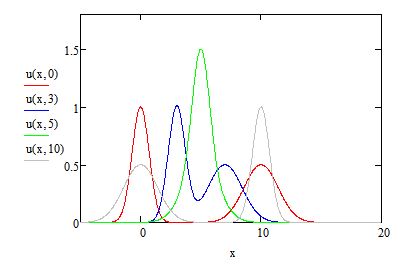
Aqui, \(F\) e \(G\) são funções arbitrárias, cada uma com um só argumento e cada uma satisfazendo independentemente à equação de onda. Qual o significado de cada uma destas funções? Consideremos \(F\left ( x-c_{s}t \right )\). Se o argumento da função, \(\xi =x-c_{s}t\), tiver um dado valor, então o valor da função \(F\left ( \xi \right )\) é o mesmo para os pontos \(x\) e instantes \(t\) tais que \(x=\xi +c_{s}t\), i.e., o valor da função é transportado para a direita com a velocidade \(c_{s}\). Assim, \(F\left ( x-c_{s}t \right )\) representa uma onda que se propaga para a direita com aquela velocidade (FIGURA 1). Analogamente \(G\left ( x+c_{s}t \right )\) representa uma onda que se propaga para a esquerda, com a mesma velocidade. Qualquer destas ondas mantem a sua forma inicial enquanto se propaga – diz-se que não há dispersão. Contudo, o campo \(u(x,t)\) é a grandeza observada e da soma daquelas funções resulta a sobreposição das ondas, alterando a forma do campo (FIGURA 1, onde, para \(t=0\), a função \(F\) está centrada em 0 e a função \(G\) está centrada em 10).

Como são determinadas estas funções?

Genericamente, qualquer campo tem que satisfazer duas condições, aqui explicitadas para o campo de deslocamentos:

1ª Condição fronteira

A que devem obedecer \(u(x,t)\) ou \(\frac{\partial u\left ( x,t \right )}{\partial t}\), em qualquer instante, nos limites do domínio onde o campo está definido?

2ª Condição inicial

Quais os dados para \(u(x,0)\) e \(\left [ \frac{\partial u(x,t)}{\partial t} \right ]_{t=0}\)?

Exemplo:

Imagine-se que o fio, de comprimento \(L\) tem os extremos livres. Então, a condição limite é:

\(\left ( \frac{\partial u(x,t)}{\partial x} \right )_{x=0}=\left ( \frac{\partial u(x,t)}{\partial x} \right )_{x=L}=0\)

Estas relações traduzem a ausência de tensões (forças) exteriores nos extremos.Considerar a Ref. 1 onde se mostrou que a tensão exercida num ponto pela parte do fio à sua direita sobre a parte à esquerda é \(\tau =E\frac{\partial u}{\partial x}\). Usando a eq. (2) e representando por uma plica a derivada em ordem a \(x\), obtém-se:

\(F'\left ( -c_{s}t \right )+G'\left ( c_{s}t \right )=0\)(3)

\(F'\left ( L-c_{s}t \right )+G'\left ( L+c_{s}t \right )=0\)(4)

Estas condições têm de ser satisfeitas qualquer que seja \(t\). Então, substituindo em (4) \(t\rightarrow t+\frac{L}{c_{s}}\) e comparando com (3), deduz-se:

\(G'\left ( c_{s}t \right )=G'\left ( c_{s}t+2L \right )\rightarrow G\left ( c_{s}t \right )=G\left ( c_{s}t +2L\right )\)

Processando do mesmo modo com \(F\), concluímos que ambas as funções são periódicas com o período \(2L\). Regressando a \(G\), esta função deverá ter a forma:

\(G\left ( c_{s}t \right )\propto e^{-ikc_{s}t}\)

com \(2kL\) múltiplo de \(2\pi\). Ora, esta função só tem um argumento: \(x+c_{s}t\), pelo que:

\(G\left ( x+c_{s}t \right )\propto e^{-ik\left ( x+c_{s}t \right )}\)

Assim, \(G'\left ( c_{s}t \right )\propto -ike^{ikc_{s}t}\). Usando eq. (3), obtém-se:

\(F'\left ( -c_{s}t \right )=ike^{ikc_{s}t}\)

Mas a função \(F\) só tem um argumento: \(x-c_{s}t\), concluindo-se:

\(F\left ( x-c_{s}t \right )\propto e^{ik\left ( x-c_{s}t \right )}\)

Assim, para estas ondas, tem-se:

\(F\left ( x-c_{s}t \right )+G\left ( x+c_{s}t \right )\propto e^{-ikc_{s}t}cos\left ( kx \right )\)

A solução geral para o campo de deslocamentos é a sobreposição destas soluções para os diferentes valores de \(k\) permitidos:

\(u\left ( x,t \right )=Re\left [ \sum_{k}^{ }a_{k}e^{-i\omega _{k}t}cos\left ( kx \right ) \right ]\)

onde se reconhece a relação de dispersão \(\omega _{k}\equiv c_{s}\left | k \right |\) entre a frequência angular das ondas e os vectores de onda \(\pm k\). As amplitudes (complexas) \(a_{k}\) são definidas pelas condições iniciais que não interessa, aqui, especificar. O leitor notará que o resultado final é o limite no contínuo da eq.(12) obtida na Ref. 1.

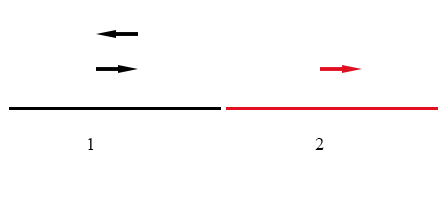
Imagine-se, agora, que o meio elástico é heterogéneo sendo constituído por uma parte (1, na FIGURA 2), com densidade \(\rho _{1}\) e módulo de Young \(E_{1}\), unida a outra parte (2, na figura), com densidade \(\rho _{2}\) e módulo de Young \(E_{2}\). Uma onda monocromática, propagando-se no meio 1, que incida na junção, não vai, apenas, criar uma onda no meio 2 (onda transmitida) como necessariamente vai gerar outra onda no meio 1 que se afasta da junção (onda reflectida). Com efeito, na junção \(\left ( x=0 \right )\), duas condições têm de ser satisfeitas:

1ª Continuidade dos deslocamentos

\(u_{1}(0,t)=u_{2}(0,t)\)(5)

Assim, como \(u_{1}(0,t)\) oscila com frequência \(\omega\), \(u_{2} (0,t)\) terá de oscilar com a mesma frequência.

2ª A tensão que, na junção, o meio 1 exerce sobre o meio 2 é igual e oposta (3ª lei de Newton) à tensão que 2 exerce sobre 1:

\(E_{1}\left ( \frac{\partial u_{1}}{\partial x} \right )_{x=0}=E_{2}\left ( \frac{\partial u_{2}}{\partial x} \right )_{x=0}\)(6)

Estas duas condições, conhecidas por relações de passagem, não podem ser verificadas, em qualquer instante, se apenas existirem ondas incidente e transmitida – é necessário considerar a onda reflectida. Temos, assim, que, no meio 1, é:

\(u_{1}(x,t)=e^{-i\omega t}\left ( e^{ik_{1}x}+Re^{ik_{1}x} \right )\)

onde \(R\) é a amplitude da onda reflectida para onda incidente de amplitude unitária e \(k_{1}=\frac{\omega }{c_{s_{1}}}\) com \(c_{s_{1}}=\sqrt{\frac{E_{1}}{\rho _{1}}}\) é a velocidade das ondas neste meio. No meio 2, é:

\(u_{2}(x,t)=Te^{-i\omega t+ik_{2}x}\)

Aqui, \(T\) é a amplitude da onda transmitida e \(k_{2}=\frac{\omega }{c_{s_{2}}}\) com \(c_{s_{2}}=\sqrt{\frac{E_{2}}{\rho _{2}}}\). As eqs. (5) e (6) determinam:

\(R=\frac{E_{1}k_{1}-E_{2}k_{2}}{E_{1}k_{1}+E_{2}k_{2}}\)

\(T=\frac{2E_{1}k_{1}}{E_{k_{1}}+E_{2}k_{2}}\)

Assim, se o meio 2 for muito mais rígido que o meio 1 (i.e. \(E_{2}\gg E_{1}\)), tem-se \(T\approx 0\) e \(R\approx -1\): quase não há onda transmitida e a onda reflectida interfere com a incidente gerando um nó de vibração na junção. Se, pelo contrário, o meio 1 for muito mais rígido que o meio 2 (i.e. \(E_{1}\gg E_{2}\)), tem-se \(T\approx 2\) e \(R\approx 1\): a junção é um ventre de vibração. A razão \(\frac{k_{1}}{k_{2}}=\frac{c_{s_{2}}}{c_{s_{1}}}\) designa-se por índice de refracção (das ondas elásticas) do meio 1 em relação ao meio 2.

Estas ondas elásticas transportam energia, o mesmo acontecendo com ondas acústicas, electromagnéticas e outras. Para encontrar o fluxo de energia destas ondas elásticas, considere-se a energia entre dois pontos fixos \(a\) e \(b>a\):

\(U(t)=\int_{a}^{b}dx\left [ \frac{1}{2}\rho \left ( \frac{\partial u}{\partial t} \right )^{2}+\frac{1}{2}E\left ( \frac{\partial u}{\partial x} \right )^{2} \right ]\)

Reconhecem-se, aqui, as contribuições das energia cinética e elástica do meio, sendo esta o limite no contínuo da energia potencial das molas consideradas na Ref. 1. Derivando a expressão anterior em ordem ao tempo e usando a equação do campo, eq. (1), obtém-se:

\(\frac{dU}{dt}=\int_{a}^{b}dx\left [ \rho \frac{\partial u}{\partial t}\frac{\partial ^{2}u}{\partial t^{2}}+E\frac{\partial u}{\partial x}\frac{\partial ^{2}u}{\partial t\partial x} \right ]=E\int_{a}^{b}dx\left [ \frac{\partial u}{\partial x}\frac{\partial ^{2}u}{\partial x^{2}}+\frac{\partial u}{\partial x}\frac{\partial ^{2}u}{\partial x^{2}}+\frac{\partial u}{\partial x}\frac{\partial ^{2}u}{\partial t\partial x} \right ]=E\int_{a}^{b}dx\frac{\partial }{\partial x}\left ( \frac{\partial u}{\partial t}\frac{\partial u}{\partial x} \right )\)

Defina-se:

\(J(x,t)=-E\frac{\partial u}{\partial t}\frac{\partial u}{\partial x}\)(7)

Assim:

\(\frac{dU}{dt}=-\int_{a}^{b}dx\frac{\partial J}{\partial x}=-J(b,t)+J(a,t)\)

Não havendo dissipação, porque deve variar esta energia no intervalo \(\left [ a,b \right ]\)? A resposta vê-se no 2º membro da equação anterior: o aumento de energia na unidade de tempo (1º membro) deve-se à entrada de energia em \(a\) e saída em \(b\). Segue-se que \(J(x,t)\) é o fluxo de energia que passa, na unidade de tempo, através do ponto \(x\), da esquerda para a direita.

A continuidade de \(J(0,t)\) na junção da FIGURA 2 está garantida pelas relações de passagem.

Para uma onda monocromática \(u(x,t)=Ae^{-i\omega _{k}t+ikc}\), é habitual considerar a média no tempo (i.e., sobre um período) do fluxo. Para isso, não é necessário tomar a parte real da expressão anterior, porque o resultado obtem-se pela expressão seguinte:

\(\left \langle J\left ( x,t \right ) \right \rangle=-\frac{1}{2}Re\left [ E\left ( \frac{\partial u}{\partial t} \right )^{*}\frac{\partial u}{\partial x} \right ]=\frac{1}{2}\left | A \right |^{2}E\omega _{k}k\)(8)

O leitor verificará facilmente que, no problema atrás analisado do fio heterogéneo, o fluxo médio da energia transportada pela onda incidente é igual à soma dos fluxos transportados pelas ondas reflectida e transmitida.

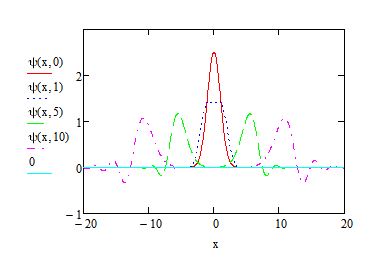
Quando a relação de dispersão não é linear, surgem novos conceitos de grande importância na transmissão de sinais. Considere-se, por exemplo, a seguinte relação: \(\omega _{k}^{2}=c_{s}^{2}k^{2}+\beta k^{4}\), com \(\beta >0\). Agora a velocidade de fase \(\frac{\omega _{k}}{k}\) depende do vector de onda: um sinal transmitido, sobreposição destas ondas, rapidamente se dispersa, dificultando, ou mesmo impossibilitando, o reconhecimento do sinal inicial (FIGURA 3).

Mas imaginemos que as ondas têm amplitudes \(A(k)\) com um pico central (em \(k_{0}\)) estreito: \(\psi \left ( x,t \right )=\int_{-\infty }^{+\infty }dkA\left ( k \right )e^{ikx-i\omega _{k}t}\)

Nesta sobreposição, ondas com \(k\) bem afastado de \(k_{0}\) praticamente não contribuem porque as respectivas amplitudes são muito pequenas. Por outro lado, para \(k\sim k_{0}\), a amplitude quase não varia junto do pico, pelo que resta considerar como varia a fase:

\(kx-\omega _{k}t\simeq k_{0}x-\omega _{k_{0}}t+\left ( k-k_{0} \right )\left ( x-\left ( \frac{d\omega _{k}}{dt} \right )_{k_{0}} \right )\)

Inserindo, obtém-se:

\(\psi \left ( x,t \right )\cong e^{ik_{0}x-i\omega _{k_{0}}t}\int_{-\infty }^{+\infty }dkA\left ( k \right )e^{i\left ( k-k_{0} \right )\left ( x-\left ( \frac{d\omega _{k}}{dt} \right )_{k_{0}}t \right )}\)

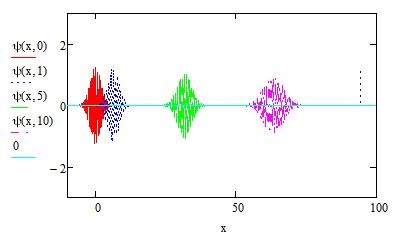
Por palavras, a onda é, essencialmente, a onda monocromática com o vector de onda do pico (designada por transportador), mas com uma amplitude (o integral acima) que a limita espacialmente, constituindo uma envolvente que se move com a velocidade \(\nu _{g}=\left ( \frac{d\omega _{k}}{dk} \right )_{k_{0}}\). O grupo de ondas desloca-se com esta velocidade de grupo (FIGURA 4). Note-se que o sinal permanece praticamente identificável ao longo do tempo. É evidente que para relações de dispersão lineares, as velocidades de fase e de grupo coincidem.

Imagine-se, agora, uma série de \(N\) linhas paralelas, no mesmo plano, equidistantes \((a)\), cada uma das quais capaz de emitir uma onda que se propaga no meio circundante. Este conjunto pode ser um genuíno emissor de ondas de som ou luz, ou ser uma rede de difracção para uma onda plana que incida sobre as linhas. Tomar-se-á a luz, aqui, como exemplo e, para simplificar, aceita-se que todas as linhas estão em fase; designe-se por \(\phi _{0}\) a amplitude da onda emitida por qualquer das linhas e por \(\lambda \) o comprimento de onda. A uma distância \(D\) do plano das linhas situa-se um plano paralelo que actua como receptor das ondas emitidas (FIGURA 5). Que se observa neste plano?

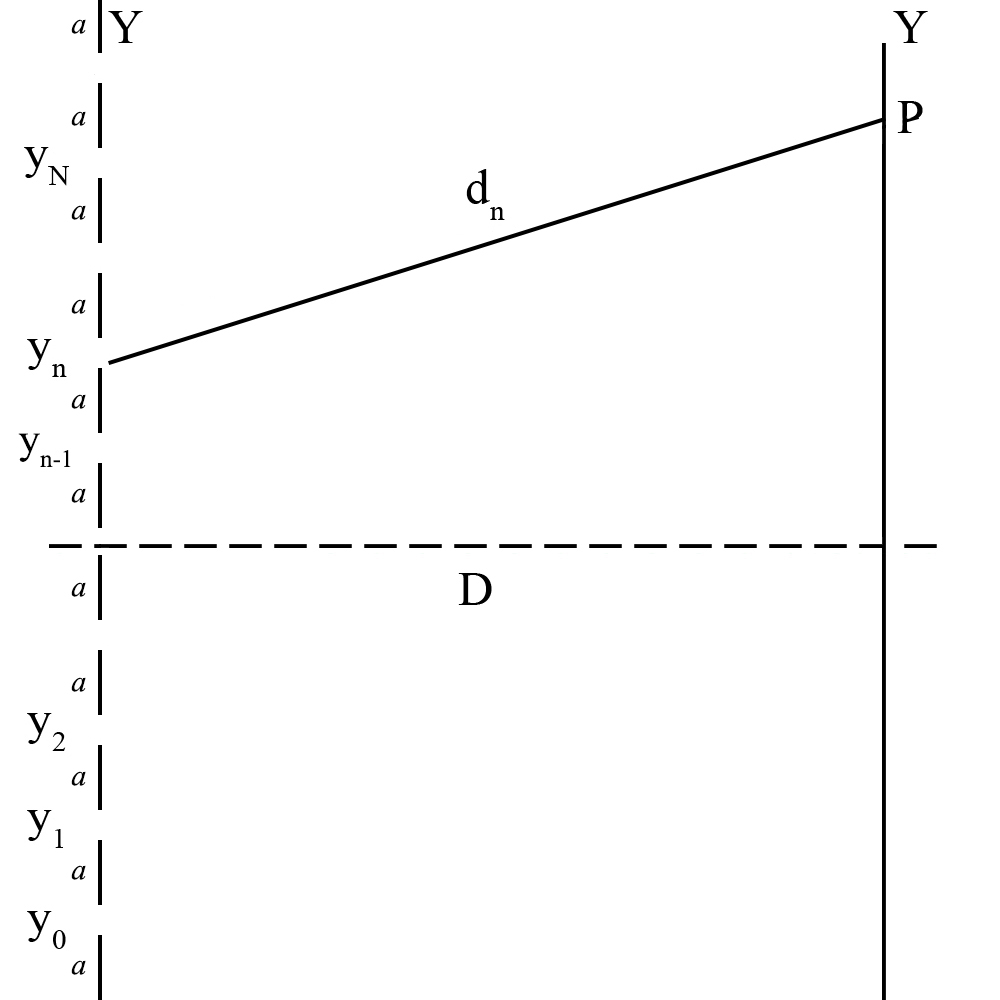
Num qualquer ponto \(P\) do receptor chegam as ondas emitidas pelas linhas, mas, agora, com fases diferentes porque têm que percorrer distâncias diferentes entre cada um dos emissores e o ponto de observação: nuns pontos, as ondas reforçam-se, originando um máximo da intensidade, noutros pontos, anulam-se mutuamente, originando um mínimo da intensidade. Deste modo, o plano receptor apresentará uma série de bandas alternando em intensidade, fenómeno conhecido por interferência, uma demonstração inequívoca de um comportamento ondulatório. Convém tomar a origem do eixo \(y\) coincidente com o ponto médio da linha dos emissores. Deste modo, a posição do emissor \(n\) é \(y_{n}=\left ( n-\frac{N+1}{2} \right )a\). Para este emissor, a distância a \(P\) é \(d_{n}=\sqrt{D^{2}+\left ( Y-y_{n} \right )^{2}}\simeq D+\frac{Y^{2}}{2D}-\frac{Yy_{n}}{D}\left ( n=1,2,...,N \right )\). Aqui, admitiu-se a situação vulgar de o plano detector se encontrar bastante longe dos emissores \(D\gg Na\). Qual a fase, em \(P\), da onda gerada pelo emissor \(n\)? Há \(\frac{d_{n}}{\lambda}\) comprimentos de onda entre emissor e \(P\); por cada um, a fase aumenta de \(2\pi\), pelo que a fase, em \(P\), é \(2\pi\frac{d_{n}}{\lambda}=kd_{n}\), onde \(k\) é o vector de onda. Assim, o emissor \(n\) contribui com \(\phi _{0}e^{ikd_{n}}\) e a amplitude total da onda é:

\(\Phi \left ( Y \right )=\phi _{0}e^{ik\left ( D+\frac{Y^{2}}{2D} \right )}\sum_{n=1}^{N}e^{-ik\frac{Yy_{n}}{D}}=N\phi _{0}e^{ik\left ( D+\frac{Y^{2}}{2D} \right )}\frac{sen\left ( k\frac{YNa}{2D} \right )}{Nsen\left ( k\frac{Ya}{2D} \right )}\)(9)

A intensidade observada em \(P\) é \(I\left ( Y \right )=\left | \Phi \left ( Y \right ) \right |^{2}\), obtendo-se:

\(I\left ( Y \right )=I_{0}\left [ \frac{sen\left ( k\frac{YNa}{2D} \right )}{Nsen\left ( k\frac{Ya}{2D} \right )} \right ]^{2}\)(10)

onde \(I_{0}=\left | N\phi _{0} \right |^{2}\) é a intensidade total emitida. Há várias observações a fazer (FIGURA 6):

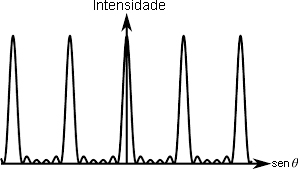
1ª É fácil ver que \(I(Y)\) é periódica sempre que \(k\frac{Ya}{2D}\) for um múltiplo de \(\pi\), apresentando máximos absolutos, iguais a \(I_{0}\) nestes pontos.

2ª Entre máximos consecutivos, a intensidade oscila,, com máximos locais (designados por 1ª ordem, 2ª ordem, etc.) e anulando-se periodicamente.

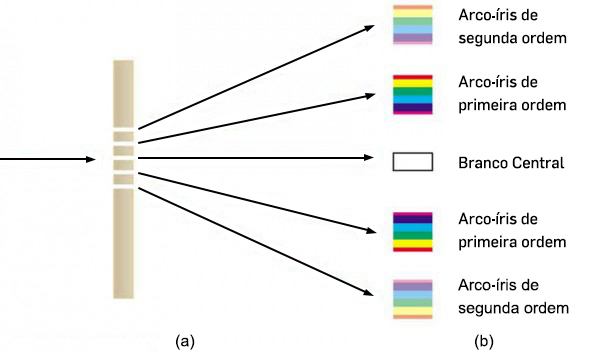
3ª A distância entre máximos depende crucialmente do comprimento de onda: quanto maior este, maior a distância entre máximos: se for emitida luz branca, o pico central \(\left ( Y=0 \right )\) é branco, mas, nos outros, os picos vermelhos estão mais afastados que os azuis (FIGURA 7), situação inversa da que ocorre na refracção da luz por um prisma de vidro. Por outro lado, quando \(\lambda \rightarrow 0\), os máximos e mínimos estão tão próximos que originam um fundo de intensidade uniforme, tal como seria previsto pela óptica geométrica – esta é, pois, o limite \(\lambda \rightarrow 0\) da óptica ondulatória.

Há um outro limite que interessa, agora considerar: \(a\rightarrow 0\) com \(Na=l\) constante e \(N\phi _{0}\rightarrow \Phi _{0}\) constante. Neste limite, o conjunto de antenas fica denso, podendo representar uma membrana que emite ondas acústicas ou uma fenda que difracta luz. A eq. (9) origina:

\(\Phi \left ( Y \right )=\Phi _{0}e^{ik\left ( D+\frac{Y^{2}}{2D} \right )}\frac{sen\left ( k\frac{Yl}{2D} \right )}{k\frac{Yl}{2D}}\)(11)

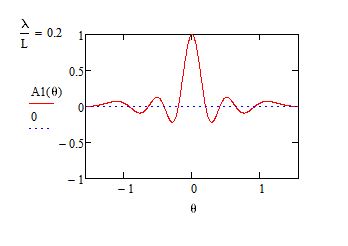
Agora, só permanece o pico central (em \(Y=0\)), seguido de oscilações cada vez mais ténues (FIGURA 8). Os primeiros anulamentos ocorrem em \(Y_{0}=\pm \frac{D}{l}\lambda\). A FIGURA 9 mostra a variação espacial da intensidade:

\(I\left ( Y \right )=I_{0}\left ( \frac{sen\left ( k\frac{Yl}{2D} \right )}{k\frac{Yl}{2D}} \right )^{2}\)(12)

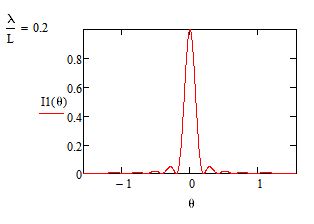
onde \(I_{0}=\left | \Phi _{0} \right |^{2}\) é a intensidade total emitida pela fenda. Os primeiros máximos secundários ocorrem para \(Y=\pm \frac{3}{2}\frac{D}{l}\lambda\), com uma intensidade \(\left ( \frac{2}{3\pi} \right )^{2}\) (cerca de 4%) menor que o pico central. Assim, a imagem da fenda tem, praticamente, a dimensão \(3\frac{D}{l}\lambda\) ou subtende o ângulo \(\frac{3\lambda}{l}\) com vértice no centro da fenda.

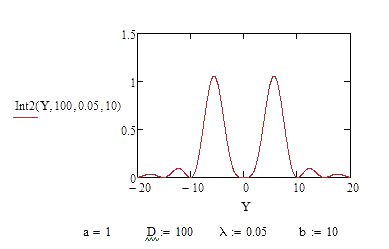
Estes resultados levantam a seguinte questão: se existirem duas fendas iguais, para simplificar, no mesmo plano, com uma distância \(b\) entre os seus centros, será possível separar as suas imagens? As ondas sobrepõem-se pelo que a sua amplitude observada é:

\(\Psi 2\left ( Y \right )=\Psi \left ( Y-\frac{b}{2} \right )+\Psi \left ( Y+\frac{b}{2} \right )\)

A intensidade respectiva:

\(I2\left ( Y \right )=\left | \Psi 2\left ( Y \right ) \right |^{2}\)

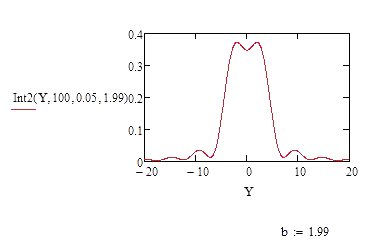
exibe claramente a interferência das duas ondas (o quadrado da soma não é a soma dos quadrados!). Na FIGURA 11, a distância entre os emissores é suficientemente grande para se perceber que há dois emissores; mas, na FIGURA 12, essa distância diminuiu o suficiente para se ficar com a dúvida se se trata da imagem de duas fendas ou, apenas, de uma. O critério de Rayleigh define essa distância mínima, identificando-a com a distância \(Y_{0}\) a que se situa o primeiro anulamento da amplitude para uma única fenda: \(b\simeq \frac{D}{l}\lambda\). É esta distância mínima, ou, de forma equivalente, a separação angular \(\alpha \), com \(sen\left ( \frac{\alpha }{2} \right )=\frac{b}{2D}=\frac{\lambda}{2l}\), entre emissores, sejam eles dois objectos observados ao microscópio ou duas estrelas observadas num telescópio, que define o poder separador do instrumento utilizado.

Estas conclusões mostram como a óptica ondulatória diverge fundamentalmente das previsões da Óptica Geométrica.

E também deve ficar claro que as conclusões obtidas aplicam-se a qualquer onda, seja qual for a sua natureza.