Uma introdução estequiométrica.

As quantidades de substâncias participantes numa reação química constituem o principal objeto de estudo da Estequiometria, um ramo da Química dedicado ao estudo das relações entre substâncias nas reações¹. O nome deriva do grego stoikheïon e métron, significando, literalmente, “medida dos elementos”².

Fundamentado na lei da conservação das massas³ e na lei das proporções definidas⁴, o cálculo estequiométrico envolve proporções e operações matemáticas simples. Excetuando os casos de reações químicas ou substâncias mais complexas, a dificuldade do tema reside quase exclusivamente na interpretação dos dados dos problemas e na execução correta de passos simples.

Suponhamos que pretendemos determinar a massa de uma substância \(A\) que reage com uma massa definida de uma substância \(B\), conforme uma reação ainda não balanceada.

\(A+B\to C+D\)

Trata-se de uma variação de problemas relativamente comuns em Estequiometria: determinar a massa de uma substância a partir de outra conhecida numa reação. O organograma da FIGURA 1 fornece um guia passo-a-passo útil para este tipo de situação.

Embora os cálculos sejam simples, existe um número significativo de etapas que tende a aumentar à medida que a complexidade do problema cresce.

Lidar com tantas etapas para um simples cálculo da massa de um reagente numa reação nos faz parecer um malabarista, tendo de equilibrar adequadamente um número grande de detalhes e este é o principal ponto de dificuldade na Estequiometria. A FIGURA 2 é uma ilustração bem-humorada das dificuldades que o cálculo estequiométrico pode acarretar.

A relação entre mole e massa das substâncias é quase sempre necessária no cálculo estequiométrico. Esta relação já foi discutida em detalhes anteriormente⁵. Note-se que, para reações estequiométricas (ou seja, aquelas cujos reagentes se encontram na proporção exata para reagirem completamente), o número de etapas reduz-se a cinco, dado que não é necessário verificar a existência de reagentes limitantes.

Considere-se o seguinte exemplo: determinar a massa de gás H₂ que reage estequiometricamente com exatos 10,0 g de gás O₂ para formar água. Por se tratar de uma reação estequiométrica, são necessárias cinco etapas para resolver este cálculo, as quais se encontram resumidas no quadro seguinte.

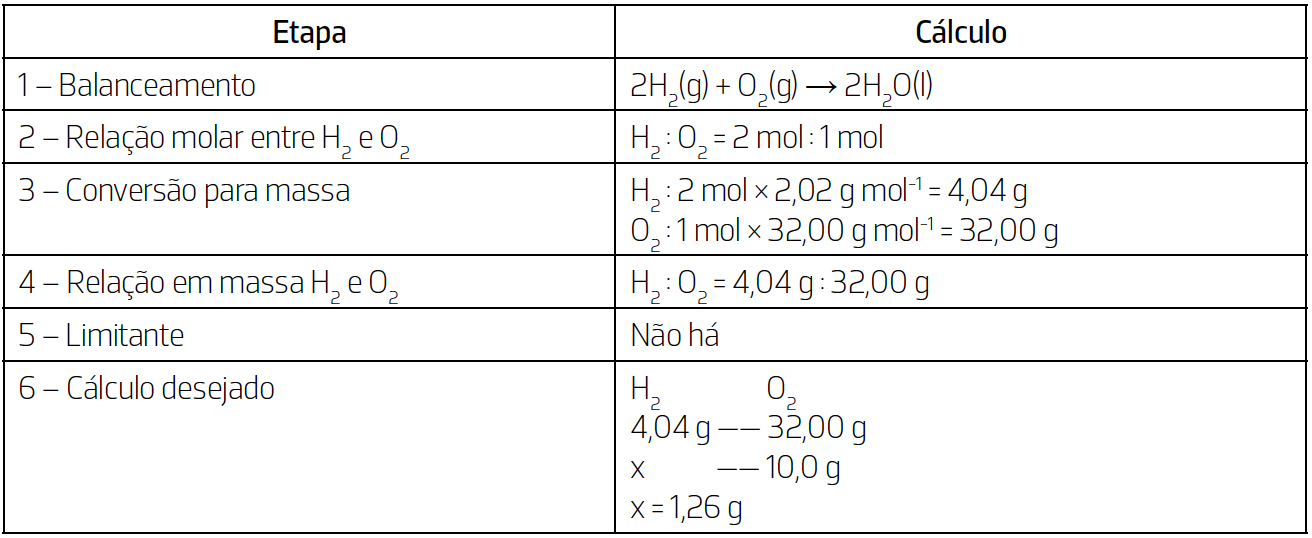
Salienta-se que o exemplo dado anteriormente é muito simples. Diversos fatores complicadores podem estar presentes, como o facto de as substâncias se encontrarem em diferentes estados físicos, a maior complexidade da reação ou essa não ser estequiométrica. Nesses casos, o cálculo torna-se mais extenso devido ao maior número de etapas.

Toda a estequiometria está fundamentada em relações matemáticas muito simples, das quais se podem obter outras relações mais elaboradas, mas extremamente úteis para realizar os cálculos. Trata-se de uma outra abordagem, que evita uma sequência de etapas e se foca num cálculo direto. A proposta deste artigo é discutir essa forma alternativa nos cálculos estequiométricos com foco nas relações fundamentais.

A relação fundamental da Estequiometria.

Considere a reação genérica

\(aA+bB\to cC+dD\)

Onde \(A\) e \(B\) são os reagentes, \(C\) e \(D\) os produtos, e os termos \(a\), \(b\), \(c\) e \(d\) são os coeficientes estequiométricos. Existe uma relação direta entre os coeficientes estequiométricos e a quantidade de moles \((n)\) de cada substância participante nesta reação, expressa da seguinte forma:

\(\frac{n_{\mathrm{A}}}{a} = \frac{n_{\mathrm{B}}}{b} = \frac{n_{\mathrm{C}}}{c} = \frac{n_{\mathrm{D}}}{d}\) (1)

onde \(n_A\), \(n_B\), \(n_C\) e \(n_D\) são, respetivamente, as quantidades em mol de \(A\), \(B\), \(C\) e \(D\) que participam da reação, ou seja, para os reagentes, correspondem à quantidade que reagiu, enquanto que para os produtos indicam a quantidade que se formou. O número limitado de substâncias serve para simplificar as expressões. A discussão apresentada aplica-se a qualquer número de substâncias participantes numa reação.

A relação (1) é fundamental para o cálculo estequiométrico, sendo aplicável a qualquer reação química e permitindo relacionar diretamente as quantidades de substâncias envolvidas. Partindo da relação apresentada, será demonstrado como é possível realizar diversos cálculos através de alguns exemplos. Por simplicidade, a maioria dos exemplos recorre a reações estequiométricas, mas o último deles envolverá o conceito de reagente limitante.

Caso 1: Relações entre as massas de substâncias nas reações.

Este é o caso mais simples, semelhante ao resolvido utilizando as etapas descritas anteriormente. Considerando a reação geral

\(aA+bB\to cC+dD\)

se desejarmos relacionar a massa de duas substâncias distintas, como por exemplo, a massa do reagente \(B(m_B)\) que reage com uma dada massa de \(A(m_A\)), devemos ter em consideração o seguinte:

\(n_\mathrm{A}=\frac{m_\mathrm{A}}{M_\mathrm{A}}\) (2)

\(n_\mathrm{B}=\frac{m_\mathrm{B}}{M_\mathrm{B}}\) (2)

Onde \(\mathrm{A}\) e \(\mathrm{B}\) são as massas molares de \(A\) e \(B\), respetivamente, em unidades de g mol^-1. Considerando apenas a parte da equação (1) que nos interessa, temos:

\(\frac{n_\mathrm{A}}{a}=\frac{n_\mathrm{B}}{b}\) (4)

A substituição direta de (2) e (3) em (4) resulta em:

\(\frac{m_\mathrm{A}}{aM\mathrm{A}}=\frac{m_\mathrm{B}}{bM\mathrm{B}}\) (5)

Que permite relacionar as massas de \(A\) e \(B\).

Problema 1: Qual a massa de H₂SO₄ que reage completamente com 10,0 g de NaOH?

Considerando a equação química balanceada:

H₂SO₄ + 2 NaOH \(\to\) Na₂SO⁴ + 2 H₂O

(os estados físicos das substâncias serão omitidos por não serem relevantes, neste caso)

Podemos escrever:

\(\frac{m_{\mathrm{H}_2\mathrm{SO}_4}}{M_{\mathrm{H}_2\mathrm{SO}_4}}=\frac{m_{\mathrm{NaOH}}}{2M_{\mathrm{NaOH}}}\) (6)

Considerando as massas molares \(M_{\mathrm{H}_2\mathrm{SO}_4}\) = 98,08 g mol^-1 e \(M_{\mathrm{NaOH}}\) = 40,00 g mol^-1, teremos, a partir de (6):

\(\frac{m_{\mathrm{H}_2\mathrm{SO}_4}}{\text{98,08 g mol}^{-1}}=\frac{\mathrm{10,0~g}}{2\times\text{40,00 g mol}^{-1}}\)

O cálculo resulta em \(m_{\mathrm{H}_2\mathrm{SO}_4}\) = 12,3 g.

Note-se como a aplicação direta da relação reduziu o número de etapas a apenas duas, ou seja: obtenção da equação balanceada e aplicação da fórmula.

Caso 2: Relações entre os volumes de soluções nas reações.

Considerando a reação geral

\(aA(aq)+bB(aq)\to cC(aq)+dD(aq)\)

Se quisermos relacionar os volumes das substâncias em duas soluções aquosas reagentes distintas, ou seja, o volume da solução de \(B(V_B\)) que reage com um dado volume da solução de \(A(V_A\)), devemos ter em consideração o seguinte:

\(c_A=\frac{n_\mathrm{A}}{V_\mathrm{A}}\) (7)

\(c_B=\frac{n_\mathrm{B}}{V_\mathrm{B}}\) (8)

Onde \(c_A\) e \(c_B\) indicam, respetivamente, as concentrações molares de \(A\) e \(B\) em unidades de mol L^-1. Das equações acima, resulta:

\(n_\mathrm{A}=c_\mathrm{A}V_\mathrm{A}\) (9)

\(n_\mathrm{B}=c_\mathrm{B}V_\mathrm{B}\) (10)

A substituição direta de (9) e (10) em (4) resulta em:

\(\frac{c_\mathrm{A}V_\mathrm{A}}{a}=\frac{c_\mathrm{B}V_\mathrm{B}}{b}\) (11)

que permite relacionar os volumes de \(A\) e \(B\) diretamente.

Problema 2: Qual o volume de uma solução de H₂SO₄ a 0,500 mol L^-1 que reage completamente com 10,0 mL de uma solução de NaOH a 1,50 mol L-1?

Note-se como este problema é consideravelmente mais complexo que o anterior, tornando a sequência de etapas da FIGURA 1 insuficiente para resolvê-lo. Caso optássemos por ela, teríamos de acrescentar mais etapas para incluir as propriedades das soluções. Vejamos como fica a resolução alternativa.

Considerando a reação química balanceada:

H₂SO₄ + 2 NaOH \(\to\) Na₂SO₄ + 2 H₂O

Podemos escrever a partir de (11):

\(c_{\mathrm{H}_2\mathrm{SO}_4}V_{\mathrm{H}_2\mathrm{SO}_4}=\frac{c_{\mathrm{NaOH}}V_{\mathrm{NaOH}}}{2}\) (12)

Substituindo:

\(\text{0,500 mol L}^{-1}\times V_{\mathrm{H}_2\mathrm{SO}_4}=\frac{1,50\mathrm{~mol~L}^{-1}\times10,0\mathrm{~mL}}{2}\)

O cálculo resulta em \(V_{\mathrm{H}_2\mathrm{SO}_4}\) = 15,0 mL.

Novamente, usa-se apenas duas etapas para se obter o resultado. Este cálculo é especialmente útil para os casos de titulações.

Caso 3: Relações entre os volumes de substâncias gasosas nas reações.

Considerando a reação geral

\(aA(g)+bB(g)\to cC(g)+dD(g)\)

Considere que queiramos relacionar os volumes de substâncias gasosas na reação, como por exemplo, qual o volume da substância \(B(V_\mathrm{B})\) a certa pressão e temperatura que reage com um dado volume da substância \(A(V_\mathrm{A})\) com suas condições e temperatura e pressão. Considerando que os gases envolvidos na reação se comportem como gases ideais, devemos ter em consideração que a equação (13) deve ser obedecida⁶:

\(pV=nRT\) (13)

Onde \(R\) é uma constante, com valor^a \(R=0,0\text{82 atm LK}^{-1}\mathrm{mol}^{-1}\). Com os devidos ajustes, podemos escrever:

\(n_\mathrm{A}=\frac{p_\mathrm{A}V_\mathrm{A}}{RT_\mathrm{A}}\) (14)

\(n_\mathrm{B}=\frac{p_\mathrm{B}V_\mathrm{B}}{RT_\mathrm{B}}\) (15)

A substituição direta de (14) e (15) em (4) resulta em:

\(\frac{p_\mathrm{A}V_\mathrm{A}}{aRT_\mathrm{A}}=\frac{p_\mathrm{B}V_\mathrm{B}}{bRT_\mathrm{B}}\) (16)

Ou melhor:

\(\frac{p_\mathrm{A}V_\mathrm{A}}{aT_\mathrm{A}}=\frac{p_\mathrm{B}V_\mathrm{B}}{bT_\mathrm{B}}\) (17)

Que permite relacionar as variáveis de \(A\) e \(B\) diretamente. Note-se que \(R\) foi eliminado da equação pois é uma constante que aparece no denominador de ambos os lados.

Problema 3: Qual o volume de N2 a 400 °C e 30,0 MPa deve ser adicionado a cada segundo em um reactor para garantir uma reação estequiométrica com um fluxo de H₂ de 10,0 L s^-1 a 200 °C e 25,0 MPa?

Note-se a complexidade do problema, embora seja uma reação estequiométrica. Considerando a reação química balanceada:

N₂ + 3 H₂\(\to\) 2 NH₃

Podemos escrever:

\( {\frac{p_{\mathrm{N}_2}V_{\mathrm{N}_2}}{T_{\mathrm{N}_2}}}={\frac{p_{\mathrm{H}_2}V_{\mathrm{H}_2}}{3T_{\mathrm{H}_2}}}\) (18)

Substituindo em (18), temos:

\(\frac{30{,}0\mathrm{~MPa}\times V_{\mathrm{N}_2}}{673\mathrm{K}}=\frac{25,0\mathrm{~MPa}\times10{,}0\mathrm{L}}{3\times473\mathrm{K}}\)

Note-se que a temperatura deve estar em K (kelvin). O cálculo resulta em \(V_{\mathrm{N}_2}\) = 3,95 L de N₂ em cada segundo.

Caso 4: Uma reação não estequiométrica que combina várias relações.

De tudo que já foi mostrado, fica evidente a praticidade do uso das relações matemáticas indicadas. Como último caso, uma situação que reúne várias relações em uma reação que não seja estequiométrica. O objetivo é verificar a validade de nossas equações em casos mais complexos.

Problema 4: Qual o volume de CO₂ liberado nas CNATP^b a partir de uma massa de 10,0 g de CaCO₃ quando esta reage com 50,0 mL de uma solução aquosa de HCl de concentração de 1,20 mol L^-1 conforme equação CaCO₃(s) + HCl(aq) CaCl₂(aq) + CO₂(g) + H₂O(l)?

Note que o problema reúne, direta ou indiretamente, todos os casos anteriores, sendo o mais complexo desta lista. Resolvê-lo empregando uma sequência de etapas certamente envolveria muitas delas. Vejamos como ele pode ser resolvido alternativamente.

Considerando a equação balanceada

CaCO₃(s) + 2HCl(aq) \(\to\) CaCl₂(aq) + CO₂(g) + H₂O(l)

da relação (4) temos:

\(n_{\mathrm{CaCO}_3}=\frac{n_{\mathrm{HCl}}}{2}=n_{\mathrm{CO}_2}\) (19)

Cada termo da igualdade se associa a uma substância. Para CaCO₃ interessa-nos uma relação de massa pelo que se utiliza a equação equivalente à (2). Para HCl interessa-nos uma relação de concentração molar, pelo que se usa a equação equivalente à (9). Já para CO₂ interessa-nos uma relação de volume gasoso, pelo que se utiliza a equação equivalente à (14). Substituindo, temos:

\(\frac{m_{\mathrm{CaCO}_3}}{M_{\mathrm{CaCO}_3}}\quad=\frac{c_{\mathrm{HCl}}V_{\mathrm{HCl}}}{2}=\frac{pV_{\mathrm{CO}_2}}{RT}\) (20)

Note-se que é uma igualdade tripla entre dois reagentes e um produto. A igualdade dupla será entre o reagente limitante e o produto. Portanto, precisamos primeiro determinar qual o reagente limitante. Para isso, aplicaremos um teste simples.

Teste para determinação do reagente limitante. Admitiremos que CaCO₃ seja o reagente limitante. Isso significa que toda a quantidade presente no problema (10,0 g) reagirá. Substituindo em (20) descobriremos qual o volume estequiométrico da solução de HCl, ou seja, o volume dessa solução que reage completamente com o sólido. Substituindo, temos:

\(\frac{10,0\mathrm{g}}{100,1\mathrm{g~mol}^{-1}}=\frac{1,20\mathrm{mol~L}^{-1}\times V_\mathrm{HCl}}{2}\)

Resolvendo, encontramos: \(V_{\mathrm{HCl}}=0{,}167\mathrm{L}=167\mathrm{mL}\). Ou seja, para reagir com toda a massa de CaCO₃ seriam necessários 167 mL da solução de HCl. Como apenas 50,0 mL estão disponíveis, conclui-se que HCl é o reagente limitante.

Desta forma, a relação que resolve nosso problema é:

\(\frac{c_\mathrm{HCl}{V_\mathrm{HCl~}}}{2}=\frac{pV_{\mathrm{CO}_2}}{RT}\) (21)

Substituindo pelos dados do problema, temos:

\(\frac{1,20\mathrm{~mol~L}^{-1}\times0{,}050\mathrm{~L}}{2}=\frac{1{,}00\mathrm{~atm}\times V_{\mathrm{CO}_2}}{0{,}082\text{ atm L K}^{-1}\mathrm{~mol}^{-1}\times298\mathrm{K}}\)

Cujo resultado é: \(V_{\mathrm{CO}_2}=0{,}733\mathrm{L}=733\mathrm{m}\mathrm{L}\).

Considerações finais.

A principal vantagem dos artifícios matemáticos está em sua capacidade de simplificação, reduzindo o número de etapas de cálculo a duas (para reações estequiométricas) ou três (para reações não estequiométricas). A sua desvantagem, no entanto, está na necessidade de manipulação matemática das equações, bem como do conhecimento prévio dessas equações. Contudo, ressalva-se que tais equações são muito simples, pelo que a metodologia se revela bastante útil, pois parte de um número reduzido de equações e permite realizar cálculos estequiométricos de maior complexidade.

Este artigo não tem como objetivo determinar qual a melhor metodologia para resolver problemas de Estequiometria, mas sim demonstrar uma alternativa ao método mais difundido. A melhor alternativa será sempre a que combinar simplicidade com melhor entendimento do leitor. Espera-se que, ao apresentar esta alternativa, o leitor esteja em melhor posição para definir a sua melhor forma de resolver problemas diversos de Estequiometria.

Notas

^a O valor de R depende das unidades adotadas. Em unidades do S.I., o valor é R = 8,314 J K^-1 mol^-1

^b Condições normais ambientais de temperatura e pressão. Isso equivale a exatos 25 °C e 1 atm.