Apesar de ser muitas vezes identificado como a força gravítica exercida pela Terra sobre o corpo, isto não é verdade. Como a Terra está em rotação, é um referencial não inercial, e os corpos à sua superfície estão sujeitos a forças inerciais, nomeadamente uma força centrífuga. Por esta razão, a aceleração de queda livre, \(\vec g\), não é o valor da aceleração devido apenas à gravidade, mas leva em conta o efeito centrífugo, pelo que é necessário especificar a latitude do local onde estamos a determinar o peso de um corpo. Esta aceleração não leva em conta efeitos como a resistência do ar, pois pode assim ser medida localmente através de experiências de queda livre num tubo de vácuo.

O peso normal de um corpo é definido como o produto da sua massa com a aceleração normal de queda livre:

\(\vec P_n = m \vec g_n\)

A aceleração normal de queda livre tem o valor \(g_n = 9,80665 m s^{-2}\), e é um valor médio das acelerações locais. O peso normal é simplesmente a definição de peso usualmente empregada, dado que na maior parte dos problemas a correcção devido à variação da força centrífuga com a latitude é desprezável.

Força centrífuga

Certamente que o leitor, ao descrever uma curva dentro de um carro, experimentou uma "força" que o empurra para o "lado de fora" da curva. Contudo, para um observador exterior ao veículo, num referencial inercial, tal força não existe e, para este observador inercial, o carro descreve a curva porque a força de atrito entre os pneus e o piso permite mudar a direcção da velocidade, acelerando-o centripetamente. No entanto, para quem está no referencial do veículo, existe a força centrífuga que deve ser considerada se se pretende estudar o movimento no referencial ligado ao carro. Tal força aparece unicamente porque o seu referencial ligado ao carro não é inercial, e é devida à inércia do corpo. O caso que acabamos de descrever ocorre também para qualquer corpo na superfície da Terra uma vez que esta tem movimento de rotação.

Consideremos um corpo na superfície da Terra, sujeito à força gravitacional, \(\vec F_g\) , e à força centrífuga, \(\vec F_c\) , como está ilustrado na figura 1. O ângulo \(\phi\) representa a latitude do local onde se encontra o corpo. No que se segue, e por simplicidade, consideraremos a Terra com a forma esférica.

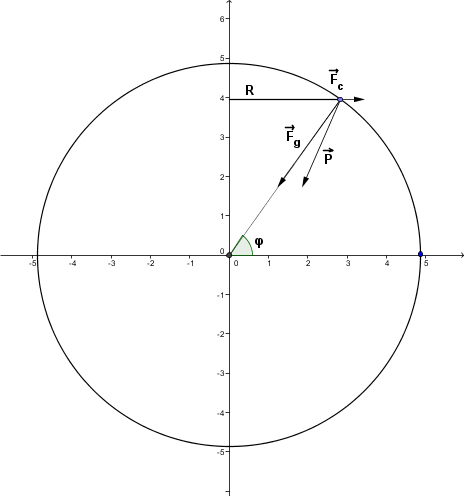
Podemos estimar o valor da força centrífuga, considerando a seguinte equação:

\(\vec F_c = - m\vec \omega \times (\vec \omega \times \vec R)\)

O vetor velocidade angular de rotação da Terra, \(\vec\omega\) é um vetor que tem a direção do eixo de rotação da Terra. Seja \(\vec R\) o vetor de posição do corpo em relação ao centro da Terra, cujo valor é igual ao raio da Terra, \(R_T\) . O valor da aceleração centrífuga é:

\(\omega^2 R_T \cos{\phi}\)

A velocidade angular da Terra tem valor \(\frac{2\pi}{24*60*60} = 7.272\times 10^{-5} rad.s^{-1}\), e o raio médio da Terra \(R_T = 6371 km\). Com estes valores é possivel determinar o valor da força centrífuga que atua no corpo para diferentes latitudes. Consideremos apenas a latitude do Pólo Norte, a latitude média de Portugal, e do Equador, para os quais temos \(\phi\) = 90º, 39º 30' e 0º, respectivamente. Utilizando os valores anteriormente apresentados, o valor da aceleração centrífuga:

\(F_{c_{PN}} = 0 m s^{-2}\)

\(F_{c_{PT}} = 0.0259 m s^{-2}\)

\(F_{c_E} = 0.0337 m s^{-2}\)

A diferença entre os valores da força centrífuga para o Equador (onde é máxima) e para Portugal corresponde a apenas 2% da aceleração normal, pelo que se justifica que nos problemas do quotidiano seja desprezada..

Vertical

É também fácil inferir que a nossa noção de vertical, a direção definida por um fio de prumo, ou a direção normal à superfície de um líquido em repouso, não é a direção do diâmetro que passa no local onde nos encontramos, mas sim a direção definida pelo peso, levando em conta o efeito da força centrífuga. Um exemplo claro deste efeito é fazer plantas crescer sobre uma base rotativa, a uma velocidade angular elevada. Estas irão crescer "para dentro", fazendo um ângulo com a vertical local. A direção de crescimento da planta em rotação define a vertical no sistema em rotação.