Fórmulas da soma e da diferenaça de dois ângulos
📧 , 📧
- * Faculdade de Ciências da Universidade do Porto
- ɫ CMUP/ Universidade do Porto
Referência Tavares, J.N., Geraldo, A., (2017) Fórmulas da soma e da diferenaça de dois ângulos, Rev. Ciência Elem., V5(3):076
DOI http://doi.org/10.24927/rce2017.076
Palavras-chave ângulos, seno, cosseno
Resumo
Adição de dois ângulos
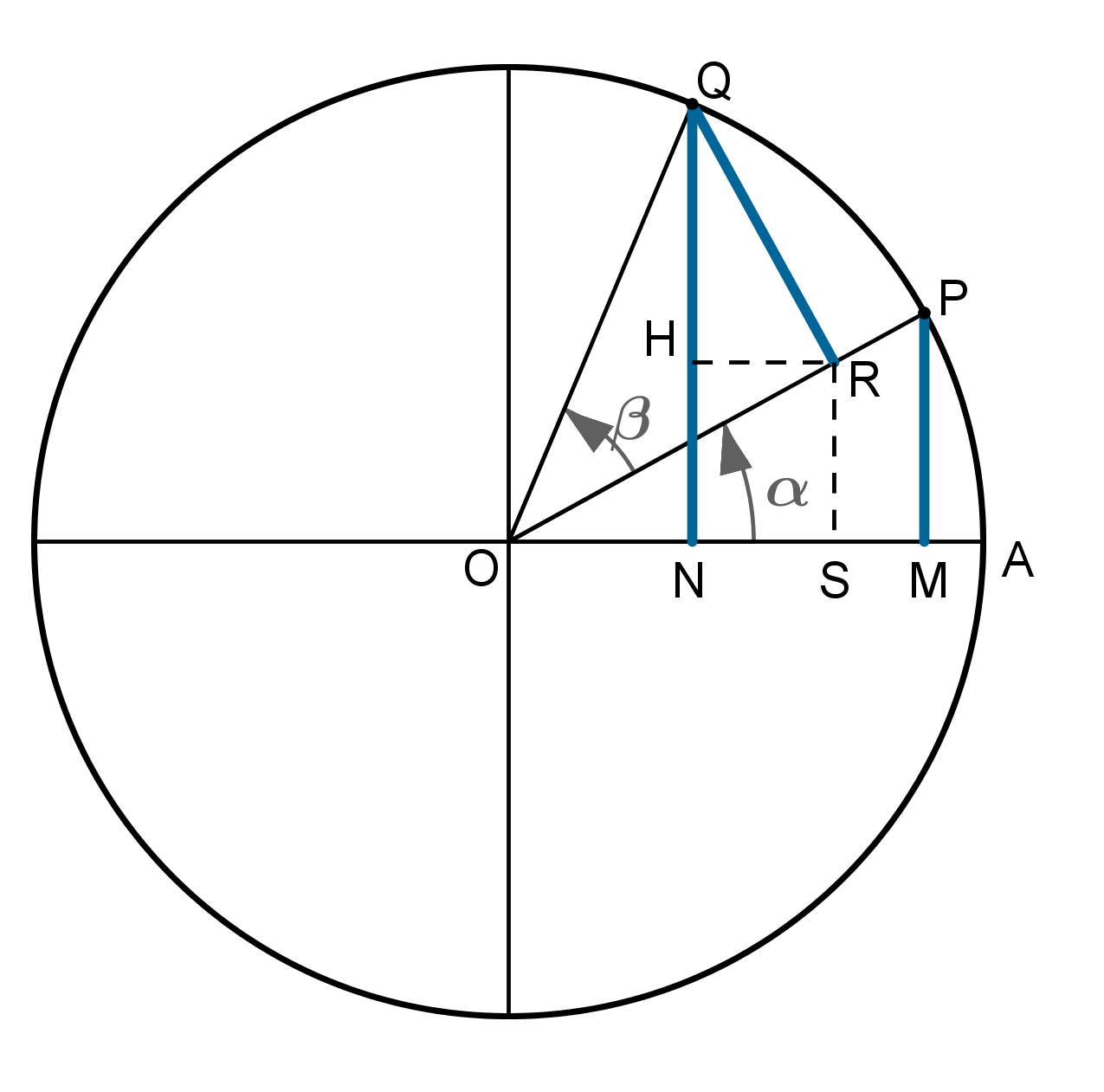
Consideremos um círculo trigonométrico e sejam \(\alpha\) e \(\beta\) dois ângulos positivos de vértice no centro \(O\) do círculo. Por simplicidade vamos considerar o caso em que a soma \(\alpha+\beta\) é menor do que \(\displaystyle \frac{\pi}{2} \mbox{ rad}\). Os outros casos tratam-se de forma análoga, recorrendo a relações trigonométricas.
Os lados extremidades dos ângulos \(\alpha\) e \(\beta\) intersectam a circunferência em dois pontos, denominados \(P\) e \(Q\), respetivamente. Por esses dois pontos, traçamos dois segmentos de reta perpendiculares a \(OA\), \([PM]\) e \([QN]\), respectivamente (Fig.1). Por \(Q\) tracemos um segmento de reta \([QR]\) perpendicular a \(OP\) e por \(R\) tracemos um segmento de reta \([HR]\) paralelo a \(OA\) e um segmento de reta \([RS]\) perpendicular a \(OA\) (ver figura 1).
Obtemos assim três triângulos retângulos \([OPM]\), \([ORS]\) e \([HQR]\) que são semelhantes.
Como se trata de um círculo cujo raio tem uma unidade, as definições de seno e cosseno de um ângulo agudo permitem-nos estabelecer as seguintes relações:
\(\sin \alpha= \overline{PM}\) ; \(\cos \alpha= \overline{OM}\) ; \(\sin \beta= \overline{QR}\) ; \(\cos \beta= \overline{OR}\)
\(\sin (\alpha+\beta)\)\(= \overline{QN}=\overline{QH}+\overline{RS}\) ; \(\cos (\alpha+\beta)\)\(= \overline{ON}=\overline{OS}-\overline{HR}\)
O facto de \([ORS]\) e \([OPM]\) serem triângulos semelhantes permite estabelecer a seguinte igualdade
\(\displaystyle \frac {\overline{RS}}{\overline{PM}}=\frac{\overline{OS}}{\overline{OM}}=\frac{\overline{OR}}{\overline{OP}}\)
que, atendendo as relações estabelecidas anteriormente é equivalente a
\(\displaystyle \frac {\overline{RS}}{\sin \alpha}=\frac{\overline{OS}}{\cos \alpha}=\frac{\cos \beta}{1}\).
Daqui resulta que, \(\overline{RS}\) \(=\sin \alpha \, \cos \beta\) e \(\overline{OS}\) \(=\cos \alpha \, \cos \beta\).
Atendendo ao facto de \([HQR]\) e \([OPM]\) também serem triângulos semelhantes podemos da mesma forma estabelecer a seguinte igualdade
\(\displaystyle \frac {\overline{HR}}{\overline{PM}}=\frac{\overline{QH}}{\overline{OM}}=\frac{\overline{QR}}{\overline{OP}}\)
que, usando as relações estabelecidas anteriormente para o seno e cosseno dos ângulos é equivalente a
\(\displaystyle \frac {\overline{HR}}{\sin \alpha}=\frac{\overline{QH}}{\cos \alpha}=\frac{\sin \beta}{1}\).
Daqui resulta que, \(\overline{HR}\)\(=\sin \alpha \, \sin \beta\) e \(\overline{QH}\)\(=\cos \alpha \, \sin \beta\).
Deduzimos então, das igualdades e relações estabelecidas anteriormente, que:
| \[\quad \sin (\alpha +\beta)=\sin \alpha \, \cos \beta + \sin \beta \, \cos \alpha \quad\] | \[\quad \cos (\alpha +\beta)=\cos \alpha \, \cos \beta - \sin \alpha \, \sin \beta \quad\] |
|---|
Sabemos ainda que, para todo o ângulo \(\alpha +\beta\) com \(\cos (\alpha+\beta) \neq 0\) se tem \(\displaystyle \tan (\alpha+\beta)=\frac{\sin (\alpha+\beta)}{\cos (\alpha+\beta}\).
Dividindo ambos os termos da fração por \(\cos \alpha \, \cos \beta\) (\(\cos \alpha \neq 0\) e \(\cos \beta \neq 0\)) a igualdade anterior é equivalente a:
| \[\quad \displaystyle \tan (\alpha+\beta)=\frac{\tan \alpha +\tan \beta}{1-\tan \alpha \, \tan \beta} \quad\] |
|---|
Uma outra prova da fórmula do seno da soma
A demostração seguinte deve-se a Volker Priebe e Edgar A. Ramos ``Proof without Words: The Sine of a Sum"; Mathematics Magazine, Vol. 73, No. 5 (Dec., 2000), p. 392. A figura fala por si:
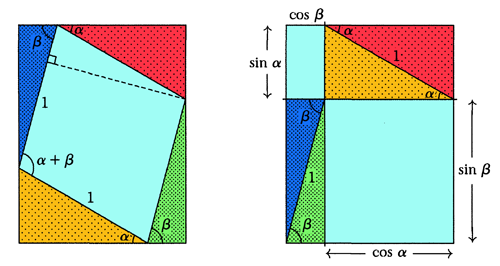
Mas eis algumas indicações:
- os dois rectângulos têm a mesma largura e o mesmo comprimento (e portanto a mesma área). Porquê?
- o quadrilátero azul claro contido no rectângulo da esquerda é um paralelogramo. Porquê? A área desse paralelogramo é igual a \(\sin(\alpha+\beta)\). Porquê?
- A área do paralelogramo azul claro contido no rectângulo da esquerda é igual à soma das áreas dos dois rectângulos azul claro contidos no rectângulo da direita. Porquê? A soma destas áreas é pois \(\sin\alpha \cos \beta + \cos\alpha \sin \beta\). Porquê?
- Portanto:
\(\sin(\alpha+\beta)= \sin\alpha \cos \beta + \cos\beta \sin \alpha \)
Subtração de dois ângulos
O problema da subtração de dois ângulos pode ser reduzido ao anterior se considerarmos a diferença \(\alpha -\beta\) como a soma do ângulo \(\alpha\) com o ângulo \(-\beta\), ou seja,
\(\sin (\alpha - \beta)=\sin \, [\alpha + (-\beta)]\, = \sin \alpha \, \cos(-\beta)+\sin (-\beta) \, \cos \alpha\quad\) como \(\quad\cos (-\beta)=\cos(\beta)\) e \(\sin (-\beta)=-\sin \beta\) temos então que:
| \[\quad \sin (\alpha - \beta)=\sin \alpha \, \cos \beta - \sin \beta \, \cos \alpha \quad\] |
|---|
Da mesma forma, temos que \(\cos (\alpha - \beta)=\cos \, [\alpha + (-\beta)]\, = \cos \alpha \, \cos(-\beta)-\sin \alpha \, \sin (-\beta)\) é então equivalente a:
| \[\quad \cos (\alpha - \beta)=\cos \alpha \, \cos \beta + \sin \alpha \, \sin \beta \quad\] |
|---|
Sabemos ainda que, para todo o ângulo \(\alpha -\beta\) com \(\cos (\alpha-\beta) \neq 0\) se tem \(\displaystyle \tan (\alpha-\beta)=\frac{\sin (\alpha-\beta)}{\cos (\alpha-\beta}\).
Dividindo ambos os termos da fração por \(\cos \alpha \, \cos \beta\) (\(\cos \alpha \neq 0\) e \(\cos \beta \neq 0\)) a igualdade anterior é equivalente a:
| \[\quad \displaystyle \tan (\alpha-\beta)=\frac{\tan \alpha -\tan \beta}{1+\tan \alpha \, \tan \beta} \quad\] |
|---|
Referências
- 1 J. Jorge G. Calado (1974) Compêndio de Trigonometria, 4ªedição. Liv. Popular de Francisco Franco, Lisboa.
Este artigo já foi visualizado 4549 vezes.



