Na referência 1, considerou-se o fluido como um sistema termodinâmico fechado (i.e., número fixo de partículas), submetido a uma pressão exterior constante, ficando indefinido o volume ocupado pelo fluido, mas que vem a ser determinado pelas condições de equilíbrio, tendo-se mostrado que a transição de fase corresponde à coexistência de duas soluções para o volume, as quais coalescem no ponto crítico. Aqui é apresentada uma outra descrição que, embora gerando os mesmos resultados que a anterior, é, contudo, suscetível de importantes generalizações que a primeira não consegue.

Esta nova descrição considera o sistema termodinamicamente aberto (i.e., número variável de partículas), ocupando um volume \(V\) fixo e em contacto com uma fonte de partículas que fixa o potencial químico exterior \((\mu _{0})\). É mostrado no Apêndice (ver eq. (A11)) que a função termodinâmica que define o equilíbrio, para volume unitário, é:

\(\psi (T,\mu _{0};n)\equiv f(T,n)-\mu _{0}n\) (1)

onde \(f(T,n) é a densidade volúmica de energia livre (de Helmholtz) do fluido e é a densidade (número de partículas por unidade de volume). Embora sejam aqui usadas as mesmas letras para funções termodinâmicas como as usadas na referência 1, deve sublinhar-se que são funções diferentes com distintos significados físicos. É esta função que determina a densidade (ou densidades) no equilíbrio com a fonte de partículas como mínimo absoluto da função \(\Psi \). Assim:

\(\frac{\partial \psi }{\partial n}=0\Leftrightarrow \frac{\partial f}{\partial n}\equiv (T,n)=\mu _{0}\) (2)

\(\frac{\partial ^{2}\psi }{\partial n^{2}}\geq 0\Leftrightarrow \frac{\partial ^{2}f}{\partial n^{2}}=\frac{\partial \mu }{\partial n}\geq 0\) (3)

Aqui, \(\mu (T,n)\) é, por definição, o potencial químico do fluido: a condição de equilíbrio expressa pela eq. (2) desempenha, no sistema aberto, o mesmo papel que a igualdade de pressões obtida na referência 1. Adicionalmente, o mínimo absoluto de \(\psi \) é, simplesmente, o negativo da pressão exercida pelo fluido, como se mostra no Apêndice (eq. (A12)):

\(\psi _{min}=-p\) (4)

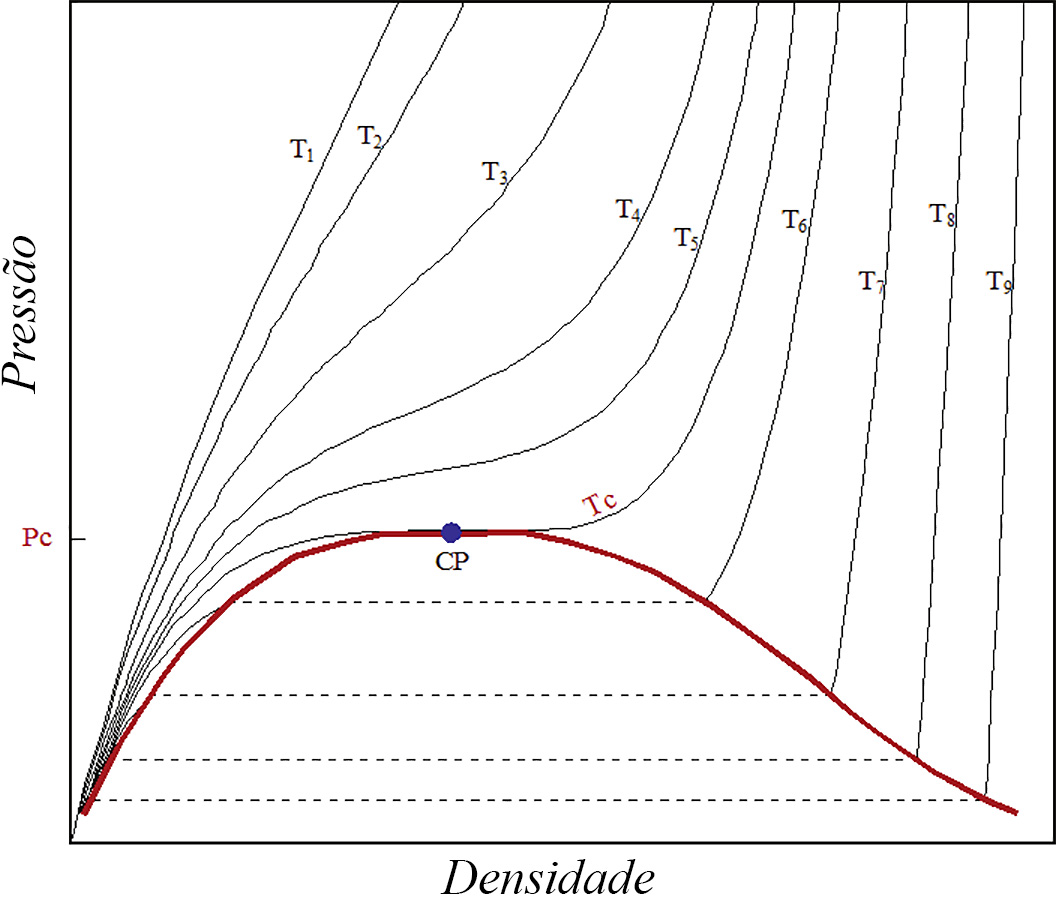
A Figura 1 exibe as isotérmicas \(p(n,T)\) para o dióxido de carbono, um exemplo do comportamento típico de muitos outros fluidos. Esta figura não é mais do que a Figura 1 na referência 1, mas onde, agora, o eixo horizontal representa a densidade. O ponto crítico é, aqui, definido pelas condições:

\(\left ( \frac{\partial p}{\partial n} \right )_{T_{c},n_{c}}=\left ( \frac{\partial ^{2}p}{\partial n^{2}} \right )_{T_{c},n_{c}}=0\) (5)

Facilmente se reconhece que são as mesmas condições invocadas na referência 1. Há várias observações a salientar nesta figura.

• Para baixas densidades e pressões e altas temperaturas \((T\gg T_{c})\), as curvas aproximam-se da equação dos gases ideais, i.e.,\(p=knT\), onde \(k\) é a constante de Boltzmann.

• Seguindo uma isotérmica acima da crítica, a pressão, para densidades elevadas, é menor que a prevista para gases ideais; tal resulta da parte atrativa do potencial entre partículas, como já foi referido na referência 2.

• Esta curvatura negativa (i.e., para baixo) é tanto mais pronunciada quanto menor for a temperatura considerada: menores temperaturas significam menores energias cinéticas médias das partículas, i.e., menores velocidades térmicas, levando as partículas a experimentarem durante mais tempo a referida parte atrativa do potencial.

• A isotérmica crítica (notada por \(T_{c}\), na figura) separa dois regimes: para temperaturas superiores, o fluido é um gás, enquanto que para temperaturas inferiores o fluido separa-se nas fases de vapor e líquida como é caracterizado, na figura, pela linha vermelha, limite dos patamares horizontais das isotérmicas.

• Abaixo da isotérmica crítica e na fase líquida, a pressão aumenta muito rapidamente com a densidade como consequência da parte fortemente repulsiva do potencial.

No que se segue, iremos, apenas, analisar o comportamento do fluido nas vizinhanças do seu ponto crítico, o qual é definido por \(T=T_{c},p=p_{c},n=n_{c}\). Mais precisamente, exigiremos \(\left | \theta \right |\ll T_{c}\) e \(\left | n' \right |\ll n_{c}\), onde \(\theta \equiv T-T_{c}\) e \(n'\equiv n-n_{c}\) medem desvios em relação ao ponto crítico. A exposição aqui seguida é conhecida por teoria de Landau^{1, 2}, reencontrando-se, sob outra forma, os resultados obtidos na referência 1.

No Apêndice mostra-se que as condições impostas pelo ponto crítico, eqs.(5), podem reescrever-se, para um sistema aberto sob a forma:

\(\left ( \frac{\partial \mu }{\partial n} \right )_{T_{c},n_{c}}=\left ( \frac{\partial ^{2}\mu }{\partial n^{2}} \right )_{T_{c},n_{c}}=0\) (6)

Então, para a isotérmica crítica e nas vizinhanças do ponto crítico, tem-se:

\(\mu (T_{c},n)=\mu _{c}+Cn'^{3}+...\)

onde \(\mu _{c}\equiv (T_{c},n_{c})\) é o potencial químico no ponto crítico e \(C\) é uma constante que se mostrará a seguir ser positiva. Com efeito, no Apêndice, é demonstrada a relação genérica (ver eq. (A6)):

\(\frac{\partial p}{\partial n}=n\frac{\partial \mu }{\partial n}\) (7)

Então, para a isotérmica crítica e nas vizinhanças do ponto crítico:

\(\left ( \frac{\partial p}{\partial n} \right )_{T_{c}}\cong n_{c}\left ( \frac{\partial \mu }{\partial n} \right )_{T_{c}}=3Cn_{c}n'^{2}\)

Ora, observando a Figura 1, vemos que \(\left ( \frac{\partial p}{\partial n} \right )_{T_{c}}\geq 0\) porque \(p(T_{c},n)\) é sempre não decrescente (a sua derivada só se anula no ponto crítico). Assim, é \(C>0\).

Consideremos uma outra isotérmica \(0\neq 0\). Agora, já deverão surgir termos lineares e quadráticos na expansão de \(\mu (T,n)\), os quais se devem anular para \(0\neq 0\). Assim, esperamos que aquela expansão tenha a forma:

\(\mu (T,n)=\mu _{c}+A\theta n'-B\theta n'^{2}+Cn'^{3}\) (8)

onde \(A\) e \(B\) são constantes positivas porque para \(\theta >0\) as isotérmicas apresentam \(p(T,n)\) a crescerem com a densidade, mas com curvatura negativa, obtendo-se o resultado por aplicação da eq. (7). Invocando a definição do potencial químico, encontramos a expansão para a energia livre:

\(\left ( \frac{\partial f}{\partial n} \right )_{T}=\mu (T,n)\rightarrow f(T,n)=f(T,n_{c})+\int_{n_{c}}^{n}dn_{1}\mu (T,n_{1})\)

Usando a eq. (8), tem-se:

\(\left ( \frac{\partial f}{\partial n} \right )_{T}=\mu (T,n)\rightarrow f(T,n)=f(T,n_{c})+\int_{n_{c}}^{n}dn_{1}\mu (T,n_{1})\) (9)

O termo cúbico pode ser eliminado com a seguinte mudança de variável:

\(n'=\frac{B\theta }{3C}+\phi \) (10)

obtendo-se:

\(f(T,n)=f(T,n_{c})+\mu _{c}\frac{B\theta }{3C}+\left ( \mu _{c}+\frac{AB\theta ^{2}}{3C} \right )\phi +\frac{A\theta }{2}\phi ^{2}+\frac{C}{4}\phi ^{4}\) (11)

tendo-se mantido, apenas, os termos de menor ordem em \(\theta \). Inserindo na eq. (1), tem-se finalmente, a função que determina o equilíbrio e que escreveremos sob forma:

\(\psi (T,\mu _{0};n)=f(T,n_{c})-\mu _{0}n_{c}-(\mu _{0}-\mu _{c})\frac{B\theta }{3C}+g(h,\phi )\) (12)

onde:

\(g(h,\phi )\equiv -h\phi +\frac{A\theta }{2}\phi ^{2}+\frac{C\phi ^{4}}{4}\) (13)

é a função de Landau³, com:

\(h=\mu _{0}-\mu _{c}-\frac{AB\theta ^{2}}{3C}\) (14)

A procura dos mínimos de \(\psi \) em ordem à densidade é equivalente à procura dos mínimos da função de Landau⁴ em ordem a \(\phi \), desempenhando o "campo" \(h\) o papel de parâmetro de controle em vez do potencial químico da fonte. A função de Landau está graficamente representada na Figura 4 e da referência 1 e, realmente, a discussão aí efetuada sobre os mínimos de \(g(h,\phi) \) pode ser totalmente recuperada no presente contexto. A principal diferença está no significado do mínimo absoluto de \(\psi \) que, aqui, é o negativo da pressão (ver eq. (4)). Este resultado permite-nos dar uma outra forma aos resultados anteriores. Com efeito, conhecemos a solução no ponto crítico (\(\theta =0;\mu _{0}=\mu _{c};n=n_{c})\) ou \(\phi =0 \)) e sabemos que aí a pressão é \(p_{c}\). Assim a eq. (12) neste caso particular, fica:

\(-p_{c}=\psi (T_{c},\mu _{c};n_{c})=f(T_{c},n_{c})-\mu _{c}n_{c}\)

Subtraindo este resultado à eq. (12), podemos escrever:

\(p_{c}-p=f(T,n_{c})-f(T_{c},n_{c})-(\mu _{0}-\mu _{c})\left ( n_{c}+\frac{B\theta }{3C} \right )+min\left [ g(h,\phi ) \right ]\)

Ora sendo \(T\approx T_{c}\), então a diferença das energia livres dá (ver eq. (A4) no Apêndice):

\(f(T,n_{c})-f(T_{c}n_{c})\cong -s(T_{c},n_{c})\theta \)

onde \(s(T_{c},n_{c})\) é a densidade volúmica de entropia no ponto crítico. Substituindo na expressão anterior, obtemos finalmente:

\(p_{c}-p=-s(T_{c},n_{c})\theta -(\mu _{0}-\mu _{c})\left ( n_{c}+\frac{B\theta }{3C} \right )+min[g(h,\phi )]\) (15)

Assim, para cada temperatura \(\theta \), o "campo" \(h\) determina o valor de \(\phi \), i.e., da densidade, que minimiza a função de Landau e o valor da função no mínimo define a pressão correspondente pela equação anterior. Em particular, para \(\theta <0\) e \(h=0\) surgem dois mínimos em \(\phi =\underline{+}\overline{\phi }\) com \(\overline{\phi }=\sqrt{\frac{A\left | \vartheta \right |}{C}}\) (ver Figura 4 da referência 1), gerando o mesmo valor da pressão – trata-se do equilíbrio das fases líquida \((+\overline{\phi })\) e vapor \((-\overline{\phi })\). Não iremos avançar com esta análise porque são reproduzidos todos os resultados encontrados na referência 1.

Generalizações

A formulação aqui apresentada, baseada no sistema aberto, é suscetível de várias importantes generalizações dificilmente implementáveis se usássemos o sistema fechado como na referência 1.

Um primeiro exemplo considera dois (ou mais) fluidos com temperaturas críticas muito próximas e que interagem quando misturados. A função termodinâmica que determina o equilíbrio é uma simples generalização da eq.(1):

\(\psi (T,\mu _{01},\mu _{02};n_{1},n_{2})=f_{1}(T,n_{1})-\mu _{01}n_{1}+f_{1}(T,n_{2})-\mu _{02}n_{2}+kn_{1}n_{2}\)

O último termo no 2º membro representa uma interação binária entre os dois fluidos, a qual pode ser repulsiva \((k>0)\) ou atrativa \((k<0)\). Como consequência desta interação, a mistura apresenta uma temperatura crítica mais elevada do que a dos seus componentes e na fase de coexistência poderão surgir comportamentos muito diferentes consoante o sinal de \(k\). O valor mínimo de \(\psi \) continua a ser o negativo da pressão exercida pela mistura. Não prosseguiremos aqui esta generalização.

Um segundo exemplo procura responder à questão: como se distribuem espacialmente as fases líquida e vapor quando coexistem em equilíbrio? É bem conhecido que, por exemplo, um campo gravítico, por pequeno que seja, determina a localização do líquido “em baixo” (menor potencial gravítico) e do vapor “em cima” (maior potencial gravítico) conseguindo, dessa forma, minimizar a energia porque o líquido é mais denso que o vapor, embora haja um aumento da energia livre de todo o fluido porque na região da transição de líquido para vapor a densidade tem de variar continuamente, i.e., existe um gradiente de densidade. É esta zona de transição que agora se pretende estudar e o termo mais simples a incluir na densidade de energia livre é \(\frac{1}{2}\alpha \left ( \frac{d\phi }{dz} \right )^{2}\), onde \(\alpha \) é uma constante positiva, não existindo termo linear por simetria. Temos, assim, que a energia livre de todo o fluido, ignorando termos independentes da densidade, é , por unidade de área do plano \(xy\)

\(F[\phi ]=\int_{-\infty }^{+\infty }dz\left [ g(0,\phi )+\frac{1}{2}\alpha \left ( \frac{d\phi }{dz} \right )^{2} \right ]\)

(Esta expressão \(F[\phi ]\) designa-se por funcional: é uma função de função. Para uma qualquer função \(\phi \left [ z \right ]\), \(F\left [ \phi \right ]\) é um número.).

Aqui, \(g(0,\phi )\) é a função de Landau definida na eq.(13) para \(h=0\) e \(\theta <0\), as duas condições que definem a coexistência de uma fase liquida (densidade \(\phi\)), com uma fase de vapor (densidade \(-\overline{\phi }\)). O objetivo é determinar a função \(\phi(z)\) que minimiza \(F[\overline{\phi }]\), sujeita às condições-fronteira:

\(\phi (z)\xrightarrow[z\rightarrow -\infty ]{ }+\overline{\phi }\)

\(\phi (z)\xrightarrow[z\rightarrow +\infty ]{ }-\overline{\phi }\)

Se \(\phi(z)\) é a solução, então qualquer acréscimo à função deve não diminuir \(F[\phi ]\). Assim, para um acréscimo muito pequeno \(\delta \phi \) a função \(\phi (z)+\delta \phi (z)\), satisfazendo às mesmas condições-fronteira (pelo que \(\delta \phi (z)\xrightarrow[z\rightarrow \underline{+}\infty ]{ }0\)) deve obrigar \(F[\phi +\delta \phi ]-F[\phi ]\) a não ter termos lineares no acréscimo, tal como no desenvolvimento de uma função junto a um mínimo não tem termos lineares. Ora:

\(F[\phi +\delta \phi ]-F[\phi ]=\int_{-\infty }^{+\infty }dz\left [ g(0,\phi +\delta \phi )-g(0,\phi )+\frac{\alpha }{2}\left ( \left ( \frac{d}{dz}(\phi +\delta \phi ) \right )^{2} -\left ( \frac{d\phi }{dz} \right )^{2}\right ) \right ]=\)

\(=\int_{-\infty }^{+\infty }dz\left [ \frac{\partial g(0,\phi)}{\partial \phi }\delta \phi (z)+\alpha \frac{d\phi }{dz}\frac{d\delta \phi }{dz} \right ]\)

onde se ignoraram termos quadráticos ou superiores no acréscimo. Integrando por partes o último termo e lembrando que o acréscimo se anula nos limites, obtemos:

\(F[\phi +\delta \phi ]-F[\phi ]=\int_{-\infty }^{-\infty }dz\left [ \frac{\partial g(0,\phi )}{\partial \phi }-\alpha \frac{d^{2}\phi }{dz^{2}} \right ]\delta \phi (z)\)

Este acréscimo da energia livre deverá ser nulo qualquer que seja \(\delta \phi (z)\). Obtemos, assim, a quação para o perfil de densidade:

\(\alpha \frac{d^{2}\phi }{dz^{2}}=\frac{\partial g(0,\phi )}{\partial \phi }=-A\left | \theta \right |\phi +C\phi ^{3}=C(-\overline{\phi }^{2}\phi +\phi ^{3})\)

A solução satisfazendo às condições-fronteira é:

\(\phi (z)=-\overline{\phi }th\left ( \frac{z-z_{0}}{\xi } \right )\)

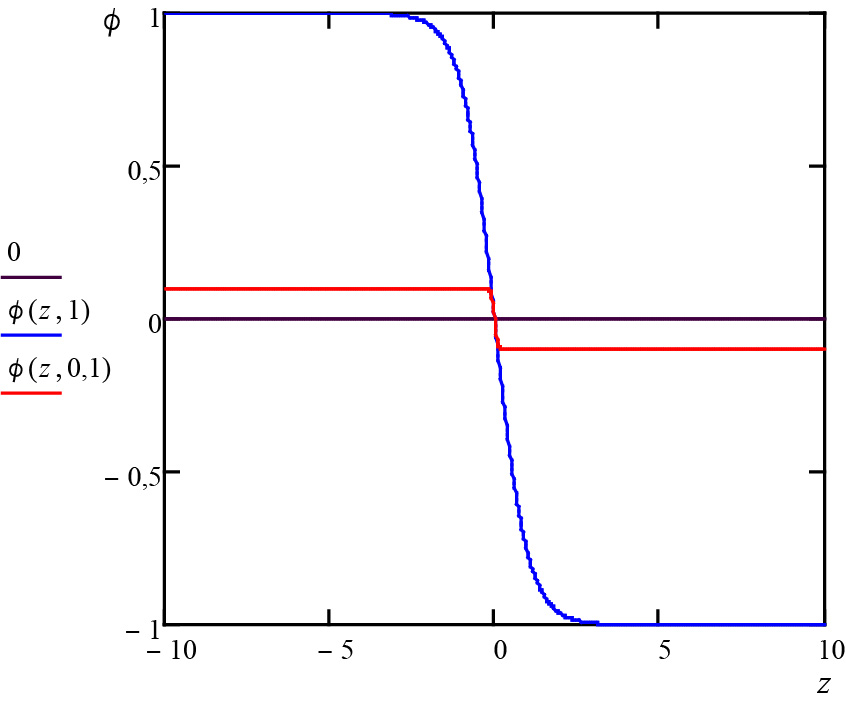
onde \(z_{0}\) é arbitrário e \(\xi =\frac{1}{\overline{\phi }}\sqrt{\frac{2\alpha }{C}}\). Este perfil está representado na Figura 2: a transição líquido para vapor efetua-se numa distância \(\xi \), em geral muito pequena, mas que diverge junto ao ponto crítico, onde, contudo, também se anula a amplitude do perfil (na figura, \(\overline{\phi }=1\) na curv azul e \(\overline{\phi }=0,1\) na curva vermelha). À medida que nos aproximamos do ponto crítico, a distinção líquido-vapor é cada vez mais ténue, ficando mais difícil estabelecer uma fronteira entre as duas fases.

Podemos, finalmente, obter o acréscimo na energia livre originada por este perfil de densidade. Para a unidade de área perpendicular ao gradiente, tem-se:

\(F[\phi (z)]-F[\overline{\phi }]=\int_{-\infty }^{+\infty }dz\left [ g(0,\phi (z))-g(0,\overline{\phi })+\frac{\alpha }{2}\left ( \frac{d\phi }{dz} \right )^{2} \right ]=\frac{2}{3}\sqrt{2\alpha \phi }^{3}\propto (T_{c}-T)^{\frac{3}{2}}\)

Esta energia livre adicional é a tensão superficial e o seu anulamento no ponto crítico é característico de transições de fase de 2ª ordem.

Apêndice: Cracterização temrodinâmica de um sistema aberto

Consideremos um sistema termodinâmico constituído por \(N\) partículas da mesma espécie química ocupando um volume \(V\) e em equilíbrio térmico com uma fonte de calor à temperatura \(T\). A função termodinâmica apropriada para caracterizar este sistema é a energia livre de Helmholtz2, \(F(T,V,N)\), cuja diferencial é:

\(dF=-SdT-pdV+\mu dN\) (A1)

Aqui, \(S\) é a entropia, \(p\) pressão e \(\mu \) o potencial química. A energia livre é uma função extensiva pelo que, para qualquer \(x>0 \), é:

\(F(T,xV,xN)=xF(T,V,N)\)

Derivando em ordem a \(x\) e pondo \(x=1\), obtemos:

\(F(T,V,N)=-pV+\mu N\) (A2)

É útil definir a densidade volúmica de energia livre:

\(f(T,n)\equiv \frac{F}{V}=-p+\mu n\) (A3)

onde \(n=\frac{N}{V}\) é a densidade (número de partículas por unidade de volume). Qual a diferencial desta função? Como \(F=Vf\), basta considerar \(V=\) constante e usar a eq. (A1), obtendo-se:

\(Vdf=-SdT+ \mu Vdn\rightarrow df= -sdT+ \mu dn\) (A4)

Aqui, \(s\equiv \frac{S}{V}\) é é a densidade volúmica de entropia. Ora, diferenciando a eq. (B3) e comparando com a eq. (A4), tem-se:

\(dp=-sdT+nd\mu\) (A5)

Esta expressão é conhecida por relação de Gibbs-Duhem. Dela decorre a expressão genérica:

\(\left ( \frac{\partial p}{\partial n} \right )_{T}=n\left ( \frac{\partial \mu }{\partial n} \right )_{T}\) (A6)

Segue-se que no ponto crítico, onde se verificam as condições (A5), é:

\left ( \frac{\partial p}{\partial n} \right )_{T_{c},n_{c}}=0\rightarrow \left ( \frac{\partial \mu }{\partial n} \right )_{T_{c},n_{c}}=0 (A7)

Derivando a eq. (A6) em ordem à densidade, tem-se:

\(\left ( \frac{\partial ^{2}p}{\partial n^{2}} \right )_{T}=\left ( \frac{\partial \mu }{\partial n} \right )_{T}+n\left ( \frac{\partial ^{2}\mu }{\partial n^{2}} \right )_{T}\)

Então, no ponto crítico:

\(\left ( \frac{\partial ^{2}p}{\partial n^{2}} \right )_{T_{c},n_{c}}=0=\left ( \frac{\partial \mu }{\partial n} \right )_{T_{c},n_{c}}+n_{c}\left ( \frac{\partial ^{2}\mu }{\partial n^{2}} \right )_{T_{c},n_{c}}\rightarrow \left ( \frac{\partial ^{2}\mu }{\partial n^{2}} \right )_{T_{c},n_{c}}=0\) (A8)

Finalmente consideremos a questão: qual a função termodinâmica que determina o estado de equilíbrio de um sistema aberto? Para isso, imaginemos que o nosso sistema pode trocar partículas com outro sistema, sendo constante o número de partículas do conjunto \((N_{0})\). Nestas condições, o equilíbrio é definido pelo mínimo (em relação a \(N\)) da função \(F(T,V,N)+F'(T,V',N')\) com \(N+N'=N_{0}\), onde \(F'\) é a energia livre do 2º sistema. Prescindindo de estudar o caso geral, consideremos, desde já, que este 2º sistema é muito maior que o sistema de interesse \((N'\gg N)\), mantendo-se sempre em equilíbrio independentemente do número de partículas trocadas. Nestas condições, este 2º sistema é designado por fonte de partículas e tem-se:

\(F'(T,V',N')=F'(T,V',N_{0}-N)\simeq F'(T,V',N_{0})-\mu _{0}N\)

onde \(\mu _{0}=\left ( \frac{\partial F'}{\partial N'} \right )_{N_{0}}\) é, pois, o potencial químico da fonte. Como \(F(T,V',N_{0})\) é independente de \(N\), o equilíbrio é, então, caracterizado pelo mínimo da função:

\(\Psi (T,\mu _{0};N)=F(T,V,N)-\mu _{0}N)\) (A9)

No mínimo deve ser:

\(\left ( \frac{\partial \Psi }{\partial N} \right )_{T,V,\mu _{0}}\rightarrow (T,n)=\mu _{0}\) (A10)

O equilíbrio é, pois, determinado pela igualdade dos potenciais químicos. Mas há outra condição de mínimo:

\(\left ( \frac{\partial ^{2}\Psi }{\partial N^{2}} \right )_{T,V,\mu _{0}}\geq 0\rightarrow \frac{\partial \mu (T,n)}{\partial n}\geq 0\)

relação conhecida por condição de estabilidade termodinâmica.

Uma vez estabelecido o equilíbrio, as eqs. (A9), (A10) e (A2) mostram que:

\(\Psi _{min}=-pV\)

Voltando ao sistema de interesse, como ovolume é mantido constante, usaremos a função:

\(\psi (T,\mu _{0};n)=\frac{\Psi }{V}=f(T,n)-\mu _{0}n\) (A11)

Esta função deve ser mínima no equilíbrio e o seu valor no mínimo é:

\(\\psi _{min}=-p\) (A12)