Os meios isotrópicos (gases, líquidos, cristais do sistema cúbico) apresentam um comportamento relativamente simples para a propagação de ondas planas e monocromáticas¹. A isotropia do meio manifesta-se na relação de dispersão² onde não intervém a direção de propagação da onda e esta direção é, também, a da propagação da energia. As propriedades óticas do meio são determinadas pelo seu índice de refração e pelos dois estados de polarização1 que podem ser escolhidos arbitrariamente no plano perpendicular ao vetor de onda.

Nos meios anisotrópicos, de que vários exemplos são dados adiante, a relação ente o deslocamento elétrico, \(\vec{D}\), e o campo elétrico, \(\vec{E}\), é tensorial³ — num qualquer sistema de eixos triretangular, essa relação escreve-se^a:

\(D_i=\varepsilon _0\varepsilon _{ij}^{'}E_j\) (1)

Admite-se aqui que o tensor permitividade elétrica relativa, \(\varepsilon _{ij}^{'}\), é simétrico pelo que é sempre diagonalizável. As suas direções próprias são ortogonais e definem o sistema de eixos dielétricos \(x_1\), \(x_2\), \(x_3\). Os correspondentes valores próprios \(\left ( \varepsilon _{1}^{'},\varepsilon _{2}^{'},\varepsilon _{3}^{'} \right )\), determinam o comportamento ótico:

meios isotrópicos \(\varepsilon _{1}^{'}=\varepsilon _{2}^{'}=\varepsilon _{3}^{'}\)

cristais uniaxiais \(\varepsilon _{1}^{'}=\varepsilon _{2}^{'}\neq \varepsilon _{3}^{'}\)

cristais biaxiais \(\varepsilon _{1}^{'}<\varepsilon _{2}^{'}<\varepsilon _{3}^{'}\)

Designam-se por índices de refração principais as raízes quadradas destes valores próprios. Deve sublinhar-se que as direções próprias são, muitas vezes, coincidentes com eixos cristalográficos e que os valores próprios dependem, em geral, da frequência da onda eletromagnética. Notar-se-á, também, que nos cristais anisotrópicos, os vetores \(\vec{D}\) e \(\vec{E}\) não são, em geral, colineares, fazendo um ângulo agudo entre eles porque a densidade de energia elétrica¹ \(\frac{1}{2}\vec{E}\cdot\vec{D}\) é sempre positiva. No entanto, aqueles vetores são colineares nos eixos dielétricos e, também, noutras direções no caso de haver degenerescência dos valores próprios.

No que se segue, e para facilitar a notação, redefine-se \(\frac{\vec{D}}{\varepsilon _0}\rightarrow \vec{D}\) e abandona-se a plica no tensor permitividade elétrica relativa. Assim, para uma onda eletromagnética plana (vetor de onda \(\vec{k}\)) e monocromática (frequência angular \(\omega\)), as equações de Maxwell dão:

\(\vec{k}\wedge \vec{E}=\omega\vec{B}\) (2)

\(\vec{k}\wedge \vec{B}=-\frac{\omega}{c^2}\vec{D}\) (3)

Segue-se que os vetores \(\vec{D}\), \(\vec{B}\), \(\vec{k}\) formam um triedro direto. O vetor de Poynting:

\(\vec{S}=\varepsilon _0c^2\vec{E}\wedge \vec{B}\) (4)

que determina a direção da propagação da energia eletromagnética, situa-se, tal como \(\vec{D}\), \(\vec{E}\), \(\vec{k}\), num plano perpendicular ao campo magnético, \(\vec{B}\) (FIGURA 1).

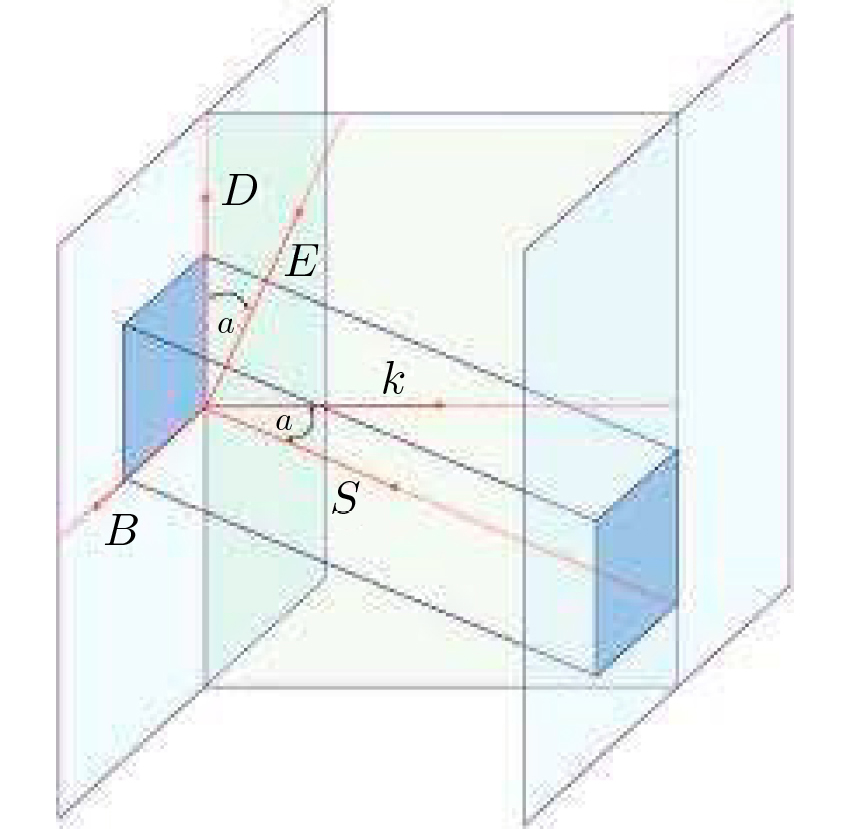
Note-se que o ângulo entre os vetores \(\vec{D}\), \(\vec{E}\) é igual ao ângulo entre os vetores \(\vec{k}\), \(\vec{S}\). A maior parte das propriedades óticas dos cristais anisotrópicos reside neste não alinhamento entre a direção de propagação da onda e a direção de propagação da energia.

Eliminando o campo magnético nas eqsuações (2) e (3), obtém-se:

\(\vec{k}^2\vec{E}-\left ( \vec{k}\cdot\vec{E} \right )\vec{k}=\frac{\omega^2}{c^2}\vec{D}\) (5)

Esta equação vai fornecer a relação de dispersão. Para isso, considere-se um sistema de eixos triretangular \(x\), \(y\), \(z\) com o eixo \(z\) alinhado na direção do vetor de onda e os eixos \(x\), \(y\) escolhidos arbitrariamente no plano perpendicular ao vetor de onda. Como é \(D_z=0\), da equação (1) tira-se \(E_z=-\frac{1}{\varepsilon _{zx}}\left ( \varepsilon _{zz}E_x+\varepsilon _{zy}E_y \right )\) que se substitui na equação (5) projetada no plano \(x\), \(y\), obtendo-se a seguinte equação sob forma matricial:

\(\frac{c^2}{\omega^2}k^2\binom{E_x}{E_y}=\begin{bmatrix} \varepsilon_{xx}-\frac{\varepsilon _{xz}}{\varepsilon _{zz}} & \varepsilon _{xy}-\frac{\varepsilon _{xz}\varepsilon _{zy}}{\varepsilon _{zz}}\\ & \\ \varepsilon _{yx}-\frac{\varepsilon _{yz}\varepsilon _{zx}}{\varepsilon _{zz}} & \varepsilon _{yy}-\frac{\varepsilon _{yz}\varepsilon _{zy}}{\varepsilon _{zz}} \end{bmatrix}\)

É uma equação de valores próprios onde a matriz no segundo membro é simétrica. A equação secular (equação de Fresnel) define então, dois valores próprios \(k^2\), distintos em geral, sendo ortogonais os respetivos vetores próprios \(\binom{E_x}{E_y}\). Note-se que tal não significa que os correspondentes vetores \(\vec{E}\) sejam ortogonais (para os quais existem, também, as componente \(E_z\)). Na verdade, o segundo membro da equação anterior define as componentes \(\binom{D_x}{D_y}\) do deslocamento elétrico, sendo, pois, os verdadeiros vetores próprios daquela equação^b. Assim, para uma direção arbitrária de propagação, há, em geral, duas ondas com a mesma frequência que se propagam naquela direção (i.e. \(k > 0\)) com diferentes vetores de onda, apresentando, pois, diferentes índices de refração, \(\eta\) (recorda-se¹ que \(k=\frac{\omega}{c}\eta\)), com polarizações \(\vec{D}\) retilíneas perpendiculares entre si e à direção de propagação, sendo também diferentes os respetivos vetores de Poynting. Há casos em que aqueles dois valores próprios são iguais, e.g., por razões de simetria nos cristais uniaxiais ou para direções particulares (binormais) nos cristais biaxiais, como se mostra adiante. Nestes casos, a ortogonalidade das polarizações pode sempre ser imposta.

Tem particular interesse projetar a equação (5) nos eixos dielétricos onde a matriz \(\left [ \varepsilon \right ]\) está diagonalizada. Obtém-se:

\(\begin{bmatrix} k^2-k_{1}^{2}-\frac{\omega^2}{c^2}\varepsilon _1 & & -k_1k_2 & & -k_1k_3\\ & & & & \\ -k_1k_2 & & k^2-k_{2}^{2}-\frac{\omega^2}{c^2}\varepsilon _2 & & -k_2k_3\\ & & & & \\ -k_1k_3 & & -k_2k_3 & & k^2-k_{3}^{2}-\frac{\omega^2}{c^2}\varepsilon _3 \end{bmatrix}\begin{bmatrix} E_1\\ E_2\\ E_3 \end{bmatrix}=0\) (6)

A matriz é simétrica; o necessário anulamento do seu determinante dá a relação de dispersão para qualquer direção, o que será apresentado mais abaixo. Genericamente, o determinante é uma função \(F\left ( \vec{k},\omega,\left [ \varepsilon \right ] \right )\) e o seu anulamento:

\(F\left ( \vec{k},\omega,\left [ \varepsilon \right ] \right )=0\) (7)

define uma superfície no espaço dos vetores de onda. É, realmente, uma superfície de duas folhas que se tocam em alguns pontos, como se verifica a seguir, designada por superfície dos vetores de onda. A normal a esta superfície é determinada pelo seu gradiente (em relação às componentes de \(k\)), i.e., \(\bigtriangledown _{\vec{k}}F\). Ora, diferenciando a função para as variáveis \(\vec{k}\) e \(\omega\), tem-se:

\(\bigtriangledown _{\vec{k}}F\cdot d\vec{k}+\frac{\partial F}{\partial\omega}d\omega=0\rightarrow \vec{v}_g=\frac{d\omega}{d\vec{k}}=-\frac{\bigtriangledown _{\vec{k}}F}{\frac{\partial F}{\partial\omega}}\) (8)

onde \(\vec{v}_g\) é a velocidade de grupo², pelo que esta é normal à superfície dos vetores de onda. A explicitação da função \(F\) torna-se mais simples se se começar por definir um vetor \(\vec{\eta}\), adimensional, da seguinte forma:

\(\vec{k}\equiv \frac{\omega}{c}\vec{\eta}\) (9)

Então, a relação de dispersão \(F = 0\) dá a equação de Fresnel:

\(\eta^2\left [ \eta_{1}^{2}\varepsilon _1+\eta_{2}^{2}\varepsilon _2+\eta_{3}^{2}\varepsilon _3-\varepsilon _1\varepsilon _2-\varepsilon _3\varepsilon _1 \right ]+\)

\(+\eta_{1}^{2}\varepsilon _2\varepsilon _3+\eta_{2}^{2}\varepsilon _3\varepsilon _1+\eta_{3}^{2}\varepsilon _1\varepsilon _2+\varepsilon _1\varepsilon _2\varepsilon _3=0\) (10)

Para uma direção arbitrária do vetor de onda definida pelo versor \(\vec{u}\), i.e., \(\vec{\eta}=\eta\vec{u}\), esta equação pode ser escrita mais sucintamente sob a forma:

\(\frac{\varepsilon _1u_{1}^{2}}{\eta^2-\varepsilon _1}+\frac{\varepsilon _2u_{2}^{2}}{\eta^2-\varepsilon _2}+\frac{\varepsilon _3u_{3}^{2}}{\eta^2-\varepsilon _3}=0\) (11)

Existem, pois, dois índices de refração, \(\eta\), para as duas ondas que se propagam naquela direção, confirmando o resultado atrás obtido, situados entre o maior e menor dos índices de refração principais (como se observa se se representar graficamente a equação (11)). A equação (10) mostra claramente que a superfície dos vetores de onda é uma superfície de duas folhas. O estudo mais atento desta superfície é apresentado mais abaixo.

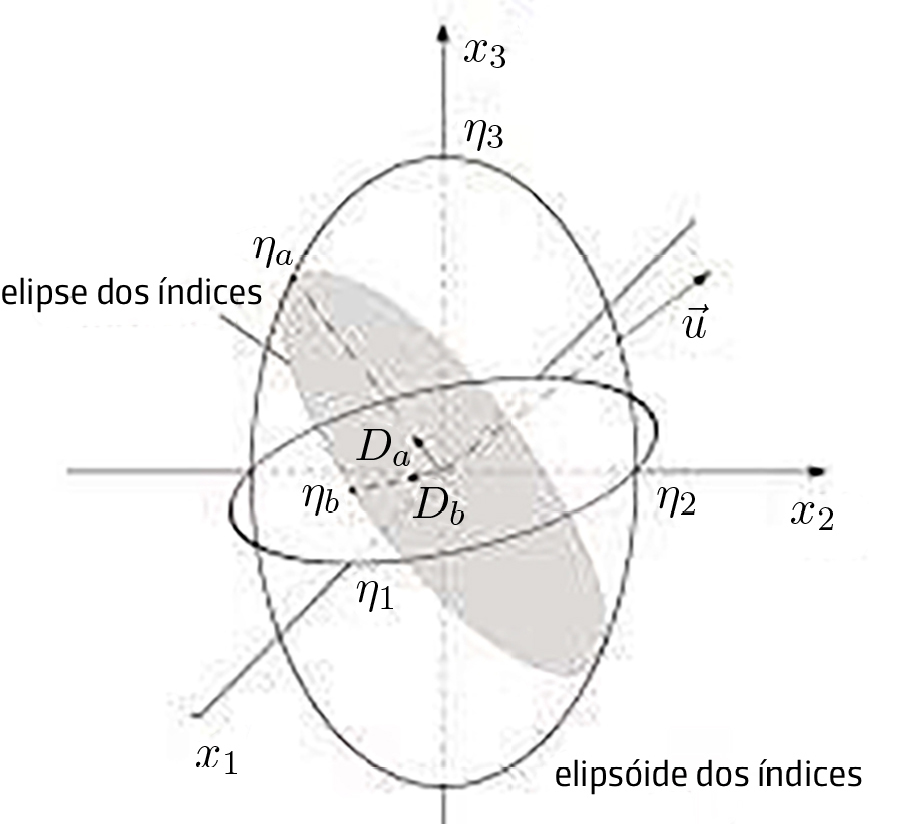
Os estados de polarização \(\vec{D}\) para as duas ondas são mais facilmente deduzido a partir do elipsoide dos índices que agora se descreve. Considere-se a energia eletrostática:

\(U_e=\frac{1}{2}\vec{E}\cdot\vec{D}=\frac{1}{2}\left ( \frac{D_{1}^{2}}{\varepsilon _1}+\frac{D_{2}^{2}}{\varepsilon _2}+\frac{D_{3}^{2}}{\varepsilon _3} \right )\)

O elipsoide dos índices é definido por:

\(\frac{\eta_{1}^{2}}{\varepsilon _1}+\frac{\eta_{2}^{2}}{\varepsilon _2}+\frac{\eta_{3}^{2}}{\varepsilon _3}=1\) (12)

Para encontrar as polarizações das duas ondas que se propagam numa direção arbitrária \(\vec{u}\), encontra-se a interseção do plano normal \(\vec{u}\) passando pela origem do elipsoide. A interseção é uma elipse, em geral, cujos semieixos são os dois índices de refração (assinalados por \(\eta_a\) e \(\eta_b\) na figura onde, também, se marcaram, nos eixos, os índices de refração principais) e também definem as duas direções de polarização (FIGURA 2). A demonstração deste resultado é apresentada no Apêndice.

Usando a equação (9), as equações (2) e (3) reescrevem-se sob a forma:

\(\vec{\eta}\wedge \vec{E}=c\vec{B}\) (13)

\(c\vec{B}\wedge \vec{\eta}=\vec{D}\) (14)

\(D_i=\varepsilon _{ij}E_j\) (15)

Um raio de luz é, realmente, um grupo de ondas com a mesma frequência, e vetores de onda distribuídos em torno de um vetor de onda \(\vec{k}\) central. Sendo um grupo de ondas, move-se com a velocidade de grupo a qual se mostrou ser normal à superfície dos vetores de onda. É, assim, de esperar que o vetor de Poynting, que exprime o transporte de energia do grupo, seja normal àquela superfície. Mas pode ser provada esta afirmação. Sejam \(\vec{E}\), \(\vec{D}\), \(\vec{B}\) os vetores do campo associados com a onda central. Para as outras ondas do grupo, haverá diferenças \(\delta\vec{E}\), \(\delta\vec{D}\), \(\delta\vec{B}\) em relação àqueles vetores. Diferenciando as equações (13) e (14), tem-se:

\(c\delta\vec{B}=\delta\vec{\eta}\wedge \vec{E}+\vec{\eta}\wedge \delta\vec{E}\)

\(\delta\vec{D}=c\delta \vec{B}\wedge \vec{\eta}+c\vec{B}\wedge \delta\vec{\eta}\)

Então:

\(c\delta\vec{B}\cdot\vec{B}=\delta\vec{\eta}\wedge \vec{E}\cdot\vec{B}+\vec{\eta}\wedge \delta\vec{E}\cdot\vec{B}=\frac{1}{\varepsilon _0c^2}\delta\vec{\eta}\cdot\vec{S}+\delta\vec{E}\cdot\vec{B}\wedge \vec{\eta}=\frac{1}{\varepsilon _0c^2}\delta\vec{\eta}\cdot\vec{S}+\frac{1}{c}\delta\vec{E}\cdot\vec{D}\)

\(\frac{1}{2}\delta\vec{D}\cdot\vec{E}=\delta\vec{B}\wedge \vec{\eta}\cdot\vec{E}+\vec{B}\wedge\delta\vec{\eta}\cdot\vec{E}=\vec{\eta}\wedge\vec{E}\cdot\delta\vec{B}+\frac{1}{\varepsilon _0c^2}\delta\vec{\eta}\cdot\vec{S}=c\delta\vec{B}\cdot\vec{B}+\frac{1}{\varepsilon _0c^2}\delta\vec{\eta}\cdot\vec{S}\)

Ora, \(\delta\vec{E}\cdot\vec{D}=\delta E_iD_i=\delta E_i\varepsilon _{ij}E_j=\delta E_j\varepsilon _{ji}E_i=E_i\varepsilon _{ij}\delta E_j=\vec{E}\cdot\delta\vec{D}\). Deste modo, as equações anteriores determinam \(\delta\vec{\eta}\cdot\vec{S}=0\), confirmando ser o vetor de Poynting normal à superfície dos vetores de onda.

Considere-se um vetor \(\vec{s}\), colinear com o vetor de Poynting, \(\vec{S}\), e satisfazendo a relação:

\(\vec{s}\cdot\vec{\eta}=1\) (16)

Quando o vetor de onda se desloca na superfície dos vetores de onda, este vetor \(\vec{s}\), normal àquela superfície, define uma outra superfície, designada por superfície dos raios, que importa agora descrever. Note-se que tal vetor, tal como \(\vec{S}\), é perpendicular aos vetores \(\vec{E}\) e \(\vec{B}\) (equação (4)). Assim, multiplicando vetorialmente por \(\vec{s}\) as equações (13) e (14), e usando a equação (16), obtém-se:

\(\vec{s}\wedge\vec{D}=c\vec{B}\) (17)

\(c\vec{B}\wedge\vec{s}=\vec{E}\) (18)

\(E_i=\left [ \varepsilon \right ]_{ij}^{-1}D_j\) (19)

onde \(\left [ \varepsilon \right ]^{-1}\) é a matriz inversa da matriz das permitividades elétricas. Estas equações são duais das equações (13)-(15): se nestas se substituir \(\vec{\eta}\rightarrow \vec{s}\), \(\vec{E}\rightarrow \vec{D}\), \(\vec{D}\rightarrow \vec{E}\) e \(\left [ \varepsilon \right ]\rightarrow \left [ \varepsilon \right ]^{-1}\), obtém-se as equações (17) a (19) (\(\vec{B}\) é invariante). Deste modo, se uma equação for obtida envolvendo as primeiras grandezas, a mesma equação será válida para as segundas grandezas, bastando efetuar a correspondente substituição. Ora, sendo \(F\left ( \vec{\eta},\left [ \varepsilon \right ] \right )=0\), a equação da superfície dos vetores de onda (equação (10)), então \(F\left ( \vec{s},\left [ \varepsilon \right ]^{-1} \right )=0\) é a equação da superfície dos raios. E tal como \(\vec{s}\) é normal à superfície dos vetores de onda, é \(\vec{\eta}\) normal à superfície dos raios. Este resultado pode ser confirmado facilmente: imagine-se que se efetua um pequeno deslocamento \(\delta\vec{\eta}\) tangente à superfície dos vetores de onda. Como \(\vec{s}\) é normal a esta superfície, então \(\delta\vec{\eta}\cdot\vec{s}=0\). Ora, da equação (16) resulta \(\delta\vec{s}\cdot\vec{\eta}=0\), i.e., o vetor de onda é normal ao correspondente pequeno deslocamento na superfície dos raios.

Cristais uniaxiais.

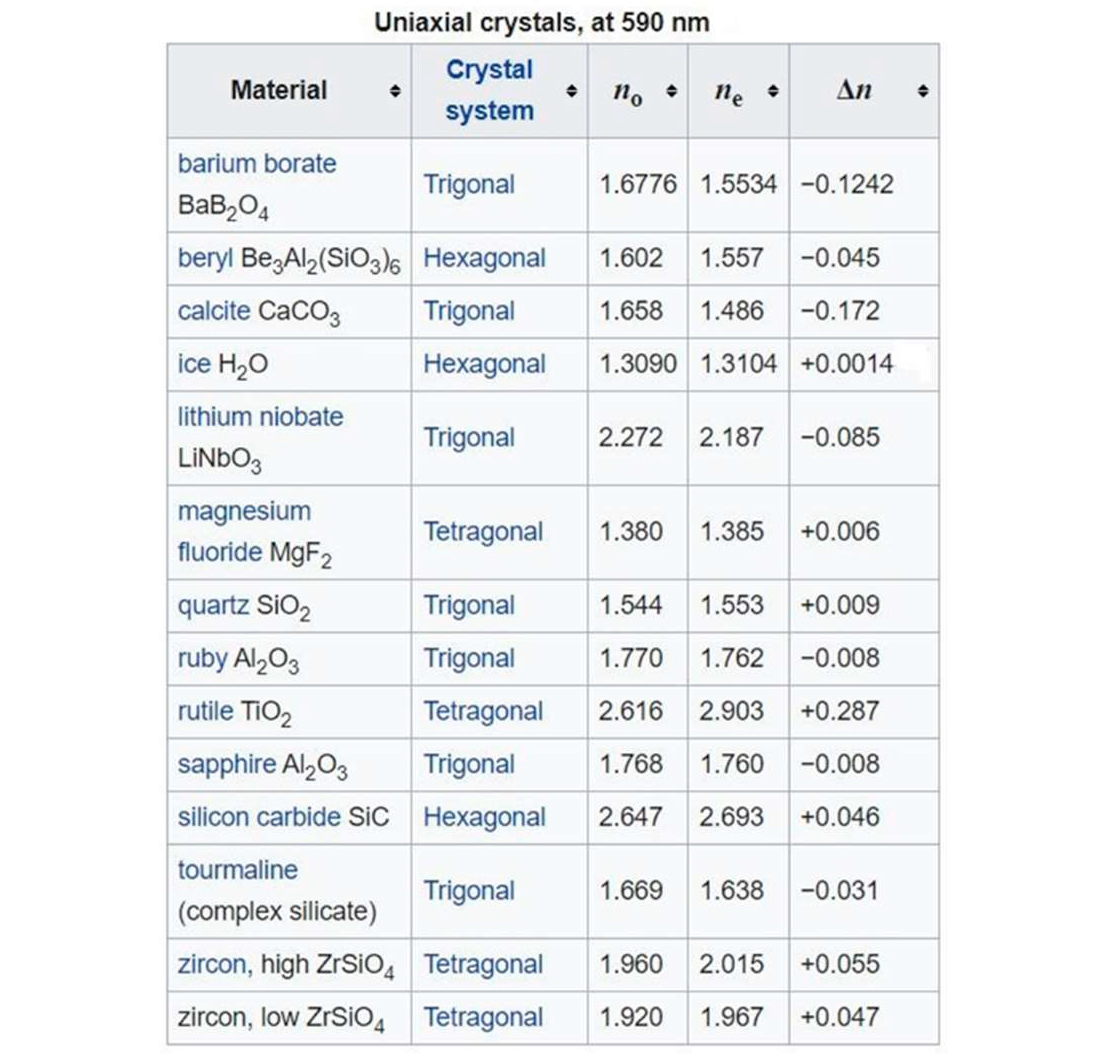
A tabela apresenta vários exemplos de cristais uniaxiais e indica os sistemas cristalográficos onde podem ocorrer. Nestes sistemas há um eixo de simetria de maior grau que se identifica, por convenção, com o eixo \(x_3\) dos eixos dielétricos, ficando os outros dois arbitrariamente escolhidos no plano perpendicular. Aquele eixo é designado por eixo ótico, sendo habitual definir \(\varepsilon _{\left | \right |}\equiv \varepsilon _3\) e \(\varepsilon _\perp\equiv \varepsilon _1=\varepsilon _2\). Embora o índice de refração dependa da direção de propagação, é costume designar os seus valores extremos por \(\eta_e=\sqrt{\varepsilon _{\left | \right |}}\) (índice extraordinário) e \(\eta_o=\sqrt{\varepsilon _{\perp}}\) (índice ordinário), dizendo-se que o cristal é opticamente positivo/negativo se \(\Delta\eta\equiv \eta_e-\eta_o\) for maior/menor do que zero.

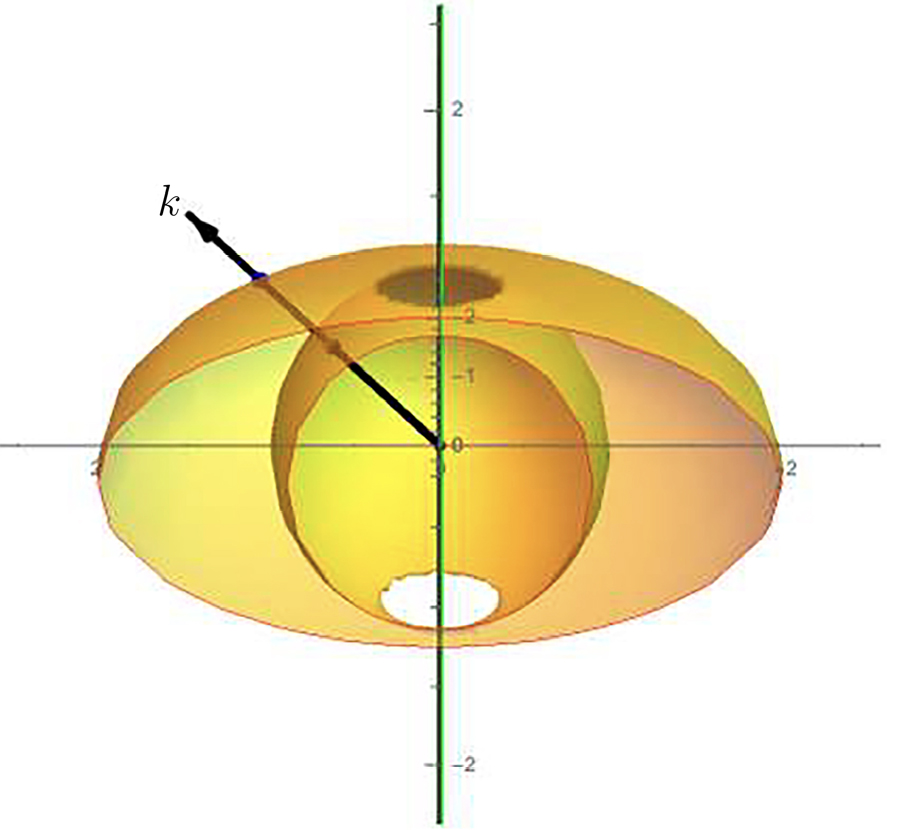
A superfície dos vetores de onda é constituída por uma esfera e por um elipsoide de revolução (FIGURA 3), em torno do eixo ótico^c, com as duas folhas a tocarem-se apenas no eixo ótico:

\(\eta_{1}^{2}+\eta_{2}^{2}+\eta_{3}^{2}=\varepsilon _\perp\)

\(\frac{\eta_{1}^{2}+\eta_{2}^{2}}{\varepsilon _{\left | \right |}}+\frac{\eta_{3}^{2}}{\varepsilon _\perp}=1\) (20)

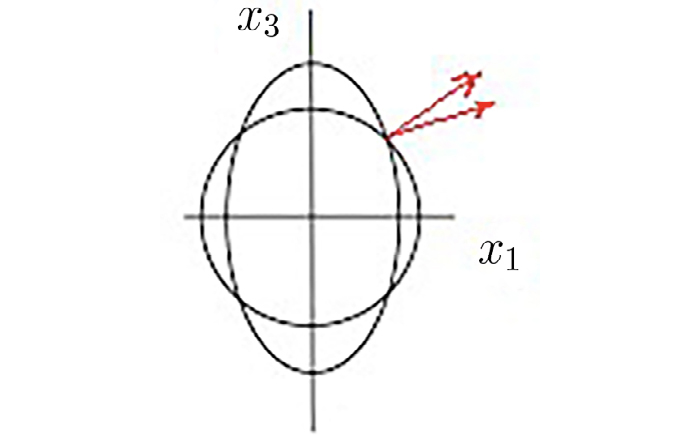
A primeira folha descreve a onda “ordinária” para a qual \(\vec{D}\) e \(\vec{E}\) são colineares e perpendiculares ao eixo ótico originando um vetor de Poynting colinear com o vetor de onda. A segunda folha descreve a onda “extraordinária”: o vetor \(\vec{D}\) situa-se no plano definido pelo eixo ótico e o vetor de onda respetivo (plano principal), não sendo colinear com \(\vec{E}\) , pelo que o vetor de Poynting, perpendicular ao elipsoide, não tem a direção do vetor de onda. O elipsoide dos índices é, também, de revolução em torno do eixo ótico e confirma estas conclusões. Assim, para luz propagando-se numa direção genérica, haverá dois raios divergentes, cada um polarizado linearmente e com polarizações perpendiculares (FIGURA 4), tal como se observa num cristal de calcite (FIGURA 5).

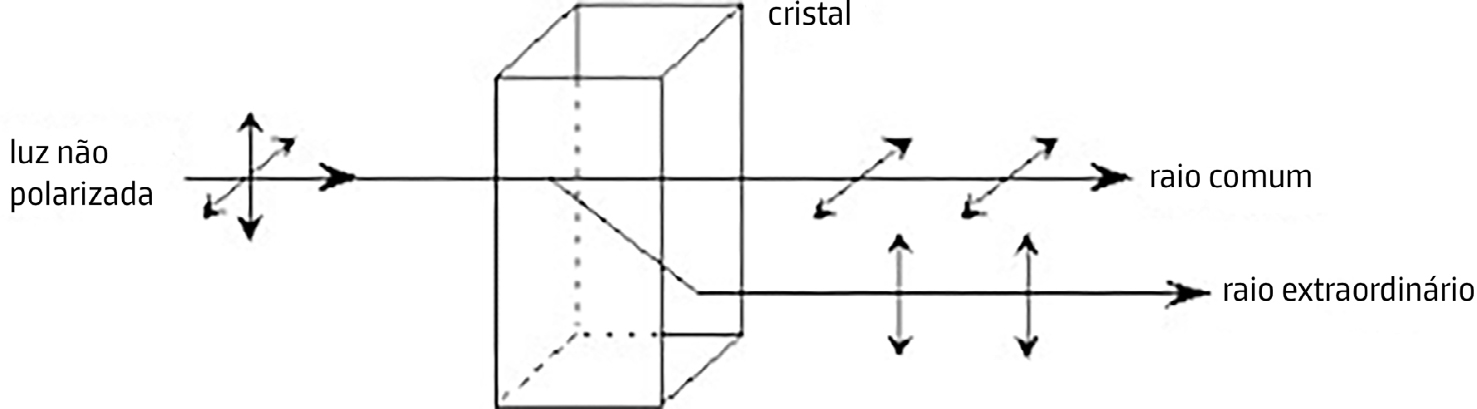
Rodando o cristal, obter-se-á um único raio quando o vetor de onda, no interior do cristal, se alinhar com o eixo ótico.

Exemplo

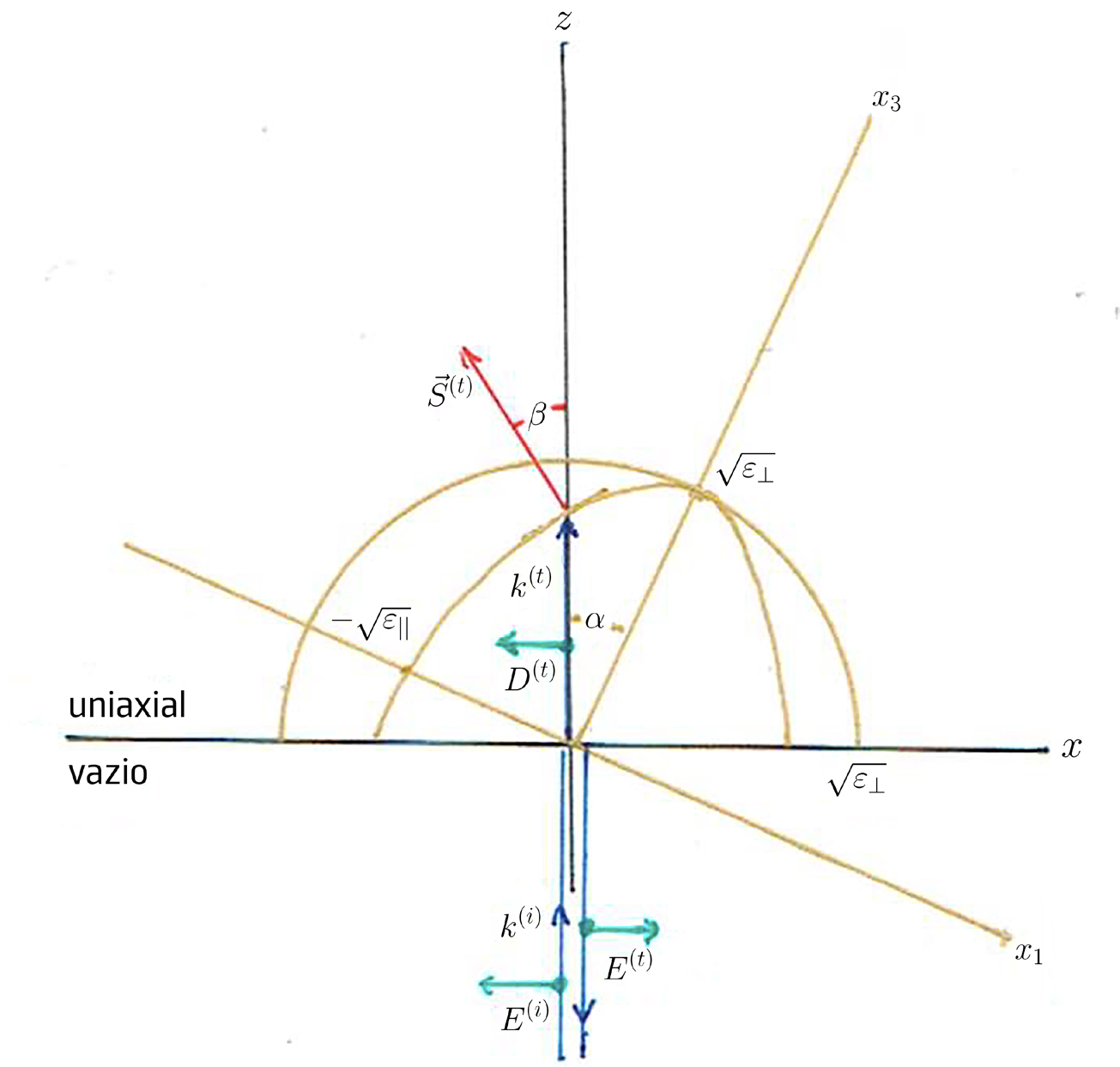
A FIGURA 6 representa a interface (eixo \(x\)) de vácuo ou ar com um cristal uniaxial. O eixo ótico, \(x_3\), situa-se no plano de incidência, fazendo um ângulo \(\alpha\) com a normal (eixo \(z\)) à interface. A interseção da superfície dos vetores de onda com o plano de incidência consiste na semicircunferência de raio \(\sqrt{\varepsilon_\perp}\) e no arco de elipse de semieixos \(\sqrt{\varepsilon _\perp}\) e \(\sqrt{\varepsilon_{\left | \right |}}\), ambos desenhados (amarelo) na figura. Uma onda plana monocromática apresenta uma incidência normal à interface (vetor de onda \(k^{\left ( i \right )}\) dirigido segundo \(z\). Pretende-se descrever as ondas refletida e transmitida.

Notar-se-á que a fase da onda incidente depende apenas do tempo no plano se separação, pelo que as ondas refletida e transmitida têm a mesma frequência e vetores de onda perpendiculares à interface¹. Para a polarização perpendicular da onda incidente, a onda transmitida também em polarização perpendicular (a polarização é normal ao eixo ótico): é o raio ordinário, apresentando índice de refração o \(\eta_o=\sqrt{\varepsilon _\perp}\) e tendo o respetivo vetor de Poynting dirigido segundo o eixo \(z\).

A caracterização completa das ondas transmitida e refletida é idêntica à encontrada para meios isotrópicos, reproduzindo-se aqui apenas a refletância e transmitância:

\(R_\perp=\left ( \frac{1-\eta_o}{1+\eta_o} \right )^2\; \; \; \; \; \; \; \; \; \; T_\perp=\frac{4\eta_o}{\left ( 1+\eta_o \right )^2}\)

Para a polarização paralela da onda incidente, os estados de polarização das três ondas estão marcados na FIGURA 6, sendo de notar que se indicou a polarização \(\vec{D}^{\left ( t \right )}\) da onda transmitida (normal ao campo magnético e ao vetor de onda \(\vec{k}^{\left ( t \right )}\). A equação da elipse nos eixos dielétricos é (ver equação (20)):

\(\frac{\eta_{1}^{2}}{\varepsilon _{\left | \right |}}+\frac{\eta_{3}^{2}}{\varepsilon _{\left | \right |}}=1\)

Ora, para a onda transmitida, \(\vec{\eta}\) tem a direção do eixo \(z\), pelo que o índice de refração da onda extraordinária é:

\(\eta^{\left ( t \right )}=\left ( \frac{\left ( \textrm{sen}\alpha \right )^2}{\varepsilon _{\left | \right |}}+\frac{\left ( \cos\alpha \right )^2}{\varepsilon _{\perp}} \right )^{-\frac{1}{2}}\) (21)

É já possível obter a direção de propagação da energia para o raio extraordinário: o vetor de Poynting é normal à elipse no ponto onde esta se cruza com o eixo \(z\). A normal à elipse tem a direção do vetor \(\left ( \frac{\eta_1}{\varepsilon _{\left | \right |}},\frac{\eta_3}{\varepsilon _{\left | \right |}} \right )\) nos eixos dielétricos \(x_1\), \(x_3\), sendo \(\eta_1=-\eta^{\left ( t \right )}\textrm{sen}\alpha\) e \(\eta_3=\eta^{\left ( t \right )}\cos\alpha\) no ponto considerado. Passando para os eixos \(x\), \(z\), esta normal tem componentes \(\left ( -\textrm{sen}\alpha\cos\alpha\left ( \frac{1}{\varepsilon _{\left | \right |}}-\frac{1}{\varepsilon _\perp} \right ),\frac{\left ( \textrm{sen} \right )^2}{\varepsilon _{\left | \right |}}+\frac{\left ( \cos\alpha \right )^2}{\varepsilon _\perp} \right )\), pelo que:

\(\textrm{tg}\beta=\eta^{\left ( t \right )^2}\textrm{sen}\alpha\cos\alpha\left ( \frac{1}{\varepsilon _{\left | \right |}}-\frac{1}{\varepsilon _\perp} \right )\) (22)

onde se usou a equação (21). Este ângulo \(\beta\) é a separação angular entre os raios ordinário e extraordinário que se observa nas FIGURA 4 e FIGURA 5.

O vetor \(\vec{D}^{\left ( t \right )}\) tem componentes \(-\vec{D}^{\left ( t \right )}\left ( \cos\alpha,\textrm{sen}\alpha \right )\) nos eixos dielétricos, pelo que o campo elétrico da onda transmitida tem componentes \(-\vec{D}^{\left ( t \right )}\left ( \frac{\cos\alpha}{\varepsilon _\perp},\frac{\textrm{sen}\alpha}{\varepsilon _{\left | \right |}} \right )\). Passando para os eixos \(x\), \(z\), obtém-se \(-\vec{D}^{\left ( t \right )}\left ( \frac{\left ( \textrm{sen}\alpha \right )^2}{\varepsilon_{\left | \right |}},\frac{\left ( \cos\alpha \right )^2}{\varepsilon_\perp},\textrm{sen}\alpha\cos\alpha\left ( \frac{1}{\varepsilon _{\left | \right |}}-\frac{1}{\varepsilon _\perp} \right ) \right )\). Assim, a continuidade, na interface, das componentes tangenciais do campo elétrico, fica:

\(E^{\left ( i \right )}-E^{\left ( r \right )}=D^{\left ( t \right )}\frac{\left ( \textrm{sen}\alpha \right )^2}{\varepsilon _{\left | \right |}}+\frac{\left ( \cos\alpha \right )^2}{\varepsilon _{\perp}}=\frac{D^{\left ( t \right )}}{\eta^{\left ( t \right )^2}}\) (23)

Os campos magnéticos das três ondas têm a direção e sentido contrário aos eixos \(y\equiv x_2\). Para a onda transmitida, o campo magnético obtém-se da equação (14): \(cB^{\left ( t \right )}=\frac{D^{\left ( t \right )}}{\eta^{\left ( t \right )}}\). Assim, a continuidade das componentes tangenciais do campo magnético, escreve-se:

\(E^{\left ( i \right )}+E^{\left ( r \right )}=\frac{D^{\left ( t \right )}}{\eta^{\left ( t \right )}}\) (24)

Das equações (23) e (24) resultam as relações de Fresnel:

\(\frac{D^{\left ( t \right )}}{E^{\left ( i \right )}}=\frac{2\eta^{\left ( t \right )^2}}{\eta^{\left ( t \right )}+1}\; \; \; \; \;\; \; \; \; \; \frac{E^{\left ( r \right )}}{E^{\left ( i \right )}}=\frac{\eta^{\left ( t \right )}-1}{\eta^{\left ( t \right )}+1}\) (25)

Conclui-se que a refletância para esta polarização da onda incidente é:

\(R_{\left | \right |}=\left ( \frac{\eta^{\left ( t \right )}-1}{\eta^{\left ( t \right )}+1} \right )^2\)

O vetor de Poynting para a onda transmitida deduz-se dos resultados anteriores, apresentando as seguintes componentes \(x\), \(z\):

\(\vec{S}_{\left | \right |}^{\left ( t \right )}=\varepsilon _0c\frac{D^{\left ( t \right )^2}}{\eta^{\left ( t \right )}}\left ( -\textrm{sen}\cos\alpha\left ( \frac{1}{\varepsilon _{\left | \right |}}-\frac{1}{\varepsilon _\perp} \right ),\frac{\left ( \textrm{sen}\alpha \right )^2}{\varepsilon _{\left | \right |}}+\frac{\left ( \cos\alpha \right )^2}{\varepsilon _\perp} \right )=\)

\(=\varepsilon _0c\frac{D^{\left ( t \right )^2}}{\eta^{\left ( t \right )}}\left ( -\textrm{sen}\cos\alpha\left ( \frac{1}{\varepsilon _{\left | \right |}}-\frac{1}{\varepsilon _\perp} \right ),\frac{1}{\eta^{\left ( t \right )^2}} \right )\)

Este resultado confirma que o vetor de Poynting é normal à elipse, como atrás encontrado. A transmitância é definida por:

\(T_{\left | \right |}=\frac{\left ( \vec{S}_{\left | \right |}^{\left ( t \right )} \right )_z}{\left (\vec{S}_{\left | \right |}^{\left ( i \right )}\right )_z}=\frac{1}{\eta^{\left ( t \right )^3}}\left ( \frac{D^{\left ( t \right )}}{E^{\left ( i \right )}} \right )=\frac{4\eta^{\left ( t \right )}}{\left ( \eta^{\left ( t \right )}+1 \right )^2}\)

verificando-se a conservação da energia: \(R_{\left | \right |}+T_{\left | \right |}=1\).

Cristais biaxiais.

A tabela apresenta vários exemplos de cristais biaxiais e indica os sistemas cristalográficos onde podem genericamente ocorrer. No sistema triclínico, os eixos dielétricos não estão relacionados com qualquer eixo cristalográfico; no sistema monoclínico, um dos eixos dielétricos, e.g., \(x_3\), coincide com o eixo de simetria de 2.ª ordem ou é perpendicular ao plano de simetria; no sistema ortorrômbico, os três eixos dielétricos coincidem com os três eixos cristalinos de 2.ª ordem. No que se segue, admite-se a ordenação \(\varepsilon _1<\varepsilon _2<\varepsilon _3\); estas constantes definem os três índices de refração principais (designados por \(\alpha\), \(\beta\), \(\gamma\) na tabela).

A superfície dos vetores de onda, equação (10), apresenta uma propriedade fundamental para a compreensão do comportamento ótico destes cristais: as duas folhas tocam-se em quatro pontos críticos, apenas, situados no plano \(x_1x_3\), simetricamente dispostos nos quatro quadrantes, definindo duas retas simétricas em relação ao eixo \(x_3\). Essas retas são designadas por eixos óticos ou binormais. Com efeito, anulando à vez cada uma das componentes do vetor \(\vec{\eta}\) na equação (10), obtém-se a interseção da superfície com os planos dielétricos. A FIGURA 7 representa as linhas obtidas no primeiro octante. Estas linhas são arcos de circunferência ou de elipse que intersectam os eixos segundo os índices de refração principais (marcados na figura).

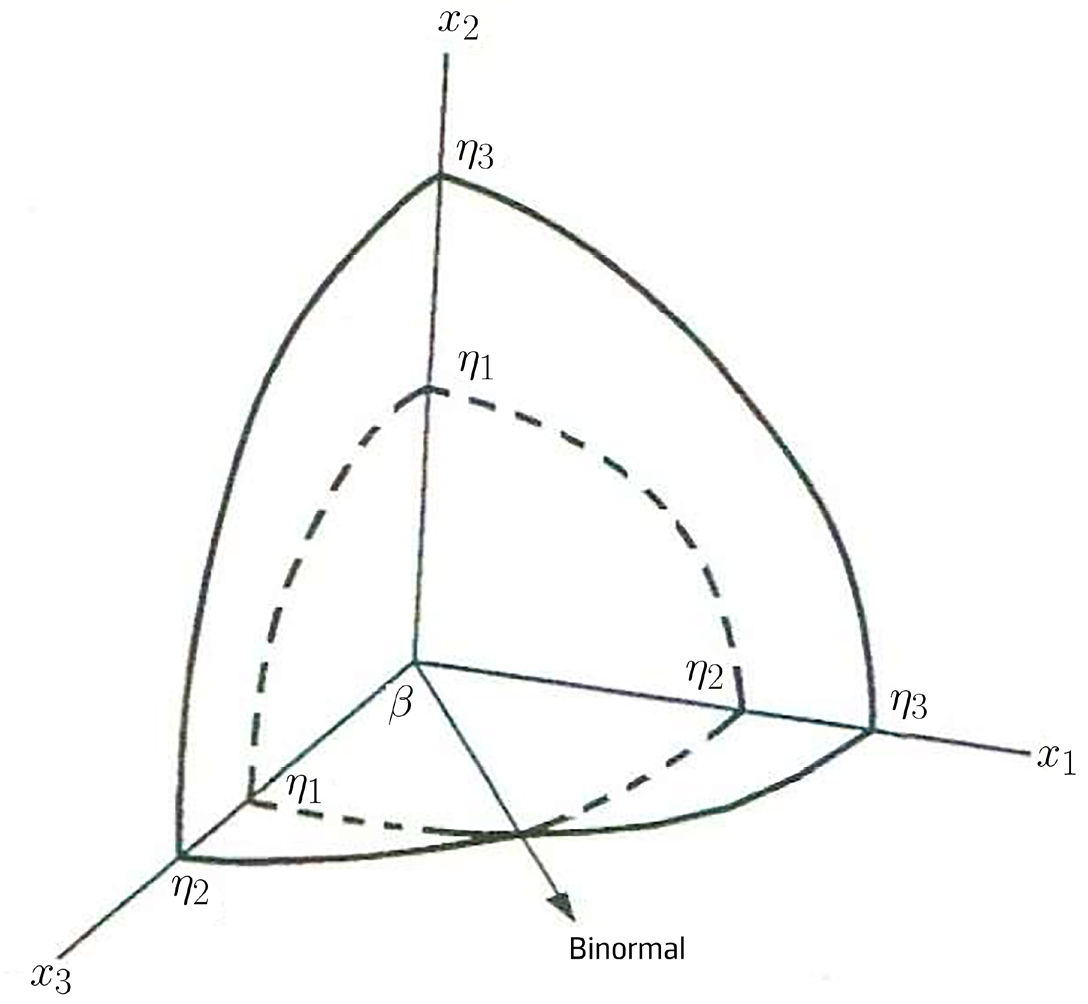
As linhas a cheio representam as interseções da folha exterior da superfície; a tracejado representam as interseções com a folha interior. As duas folhas tocam-se num único ponto neste quadrante do plano \(x_1x_3~\), definindo a binormal. Há três outros pontos similares nos outros quadrantes, como se mostra na FIGURA 8.

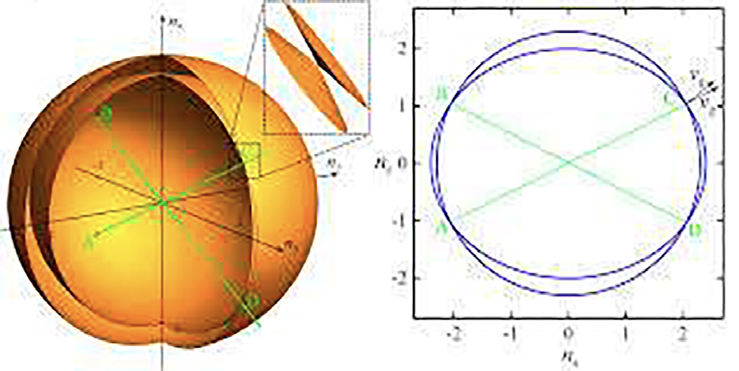
É fácil encontrar as coordenadas deste pontos pois que resultam da interseção da circunferência de raio \(\sqrt{\varepsilon _2}\) com a elipse de semieixos \(\sqrt{\varepsilon _1}\) e \(\sqrt{\varepsilon _3}\), obtendo-se:

\(\eta_{1}^{2}=\varepsilon _3\frac{\varepsilon _2-\varepsilon _1}{\varepsilon _3-\varepsilon _1}\; \; \; \; \; \; \; \; \; \; \eta_{3}^{2}=\varepsilon _1\frac{\varepsilon _3-\varepsilon _2}{\varepsilon _3-\varepsilon _1}\) (26)

Daqui resulta o ângulo \(\beta\) que a binormal faz com o eixo \(x_3\):

\(\textrm{tg}\beta=\sqrt{\frac{\varepsilon _3}{\varepsilon _1}\frac{\varepsilon _2-\varepsilon _1}{\varepsilon _3-\varepsilon _2}}\) (27)

Os pontos críticos são pontos especiais: nas suas vizinhanças, as normais à superfície (em número infinito) dispõem-se em cone, como se percebe na FIGURA 8. A interseção deste cone no primeiro quadrante do plano \(x_1x_3\) está definido pelas duas setas vermelhas da FIGURA 9: uma normal ao arco de circunferência (com a direção, pois, da binormal) e a outra normal ao arco de elipse.

A importância de um ponto crítico percebe-se se se imaginar que se corta o cristal sob a forma de uma lâmina de faces paralelas e perpendiculares a uma binormal. Efetuando a incidência normal de uma luz natural, de modo que a sua polarização elétrica flutua aleatoriamente no plano perpendicular à direção de propagação, a onda transmitida tem a extremidade do seu vetor de onda no ponto crítico e os raios (vetores de Poynting), normais à superfície dos vetores de onda, distribuem-se em cone — é a refração cónica interna. Na face de saída, obtém-se uma distribuição cilíndrica de radiação paralela à binormal (FIGURA 10).

A superfície dos raios, dual da superfície dos vetores de onda, apresenta propriedades similares, exibindo quatro pontos críticos no plano \(x_1x_3\), definindo duas retas designadas por bi-radiais fazendo um ângulo \(\gamma\) com o eixo \(x_3\) que, por dualidade, se deduz a partir da equação (27):

\(\textrm{tg}\gamma=\sqrt{\frac{\varepsilon _1}{\varepsilon _3}}\textrm{tg}\beta\; \; \; \; \; \rightarrow \; \; \; \; \; \gamma<\beta\) (28)

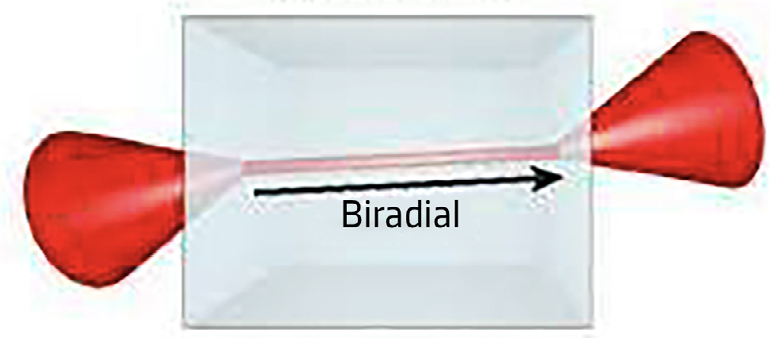
Num ponto crítico da superfície dos raios há uma infinidade de normais dispostas em cone e que são o lugar geométrico dos vetores de onda associados com o mesmo vetor \(\vec{s}\) dirigido segundo a bi-radial, com extremidade no ponto crítico, estando um desses vetores de onda alinhado com a bi-radial. Considere-se uma lâmina de faces paralelas do mesmo cristal as quais são perpendiculares à bi-radial. Cobrindo a face de entrada excepto num pequeno círculo onde, com uma lente, se faz convergir luz de modo que os vetores de onda refractada se situem no referido cone, a radiação no interior do cristal apresenta um único raio que, ao atingir a face de saída, origina um feixe divergente, em cone, da radiação — é a refração cónica externa (FIGURA 11).

A FIGURA 12 resume a relação entre a superfície dos vetores de onda (azul) e a superfície dos raios (verde) nas suas interseções com o plano \(x_1x_3\), indicando-se a tracejado as respetivas folhas internas (as escalas são diferentes para as duas superfícies). Desenharam-se a binormal (vermelho) e bi-radial (amarelo).

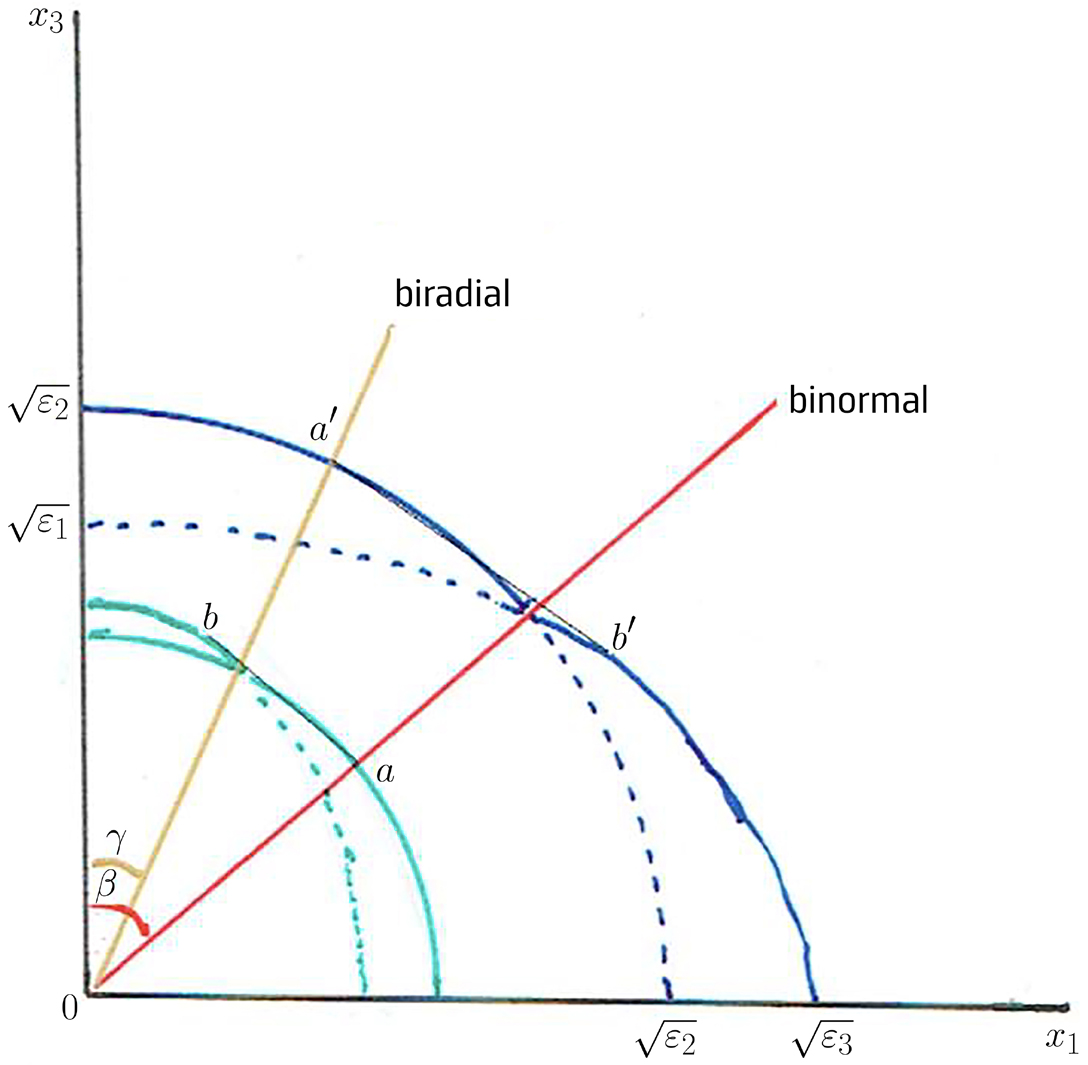
O ponto a é a interseção da binormal com a superfície dos raios. O vetor de onda dirigido segundo a binormal é perpendicular em \(a\) à superfície dos raios. O plano tangente a esta superfície em \(a\) é também tangente em \(b\), pelo que os raios \(Oa\) e \(Ob\) estão associados com o mesmo vetor de onda (dirigido segundo a binormal). Assim, \(Oab\) é a interseção com o plano da figura do cone de refração cónica interna. De modo análogo, o ponto \(a′\) é a interseção da bi-radial com a superfície dos vetores de onda. Como a bi-radial tem a direção de um raio, é normal àquela superfície. Assim, traçando o plano tangente à superfície dos vetores de onda em \(a′\), ele volta a ser tangente a esta superfície em \(b′\). Tal significa que os vetores de onda \(Oa′\) e \(Ob′\) admitem a mesma normal (o raio dirigido segundo a bi-radial) à superfície dos vetores de onda. Logo, \(Oa′b′\) é a interseção com o plano da figura do cone de refração cónica externa.

A birrefringência é usada em écrans de cristais líquidos (LCD), em lentes polaroid e em técnicas de diagnóstico em Medicina. O plástico, sob tensão, é birrefringente revelando-se útil em Engenharia Civil para avaliar zonas sob elevada tensão em modelos, à escala reduzida, de pontes e barragens hidroelétricas, uma técnica designada por fotoelasticidade. Em Mineralogia é empregue para identificar rochas, minerais e pedras preciosas. Em Geofísica é utilizado para estudar as ondas-S (transversais) que se propagam apenas na parte sólida da Terra.

Apêndice.

Propriedades do elipsoide dos índices.

O elipsoide dos índices é definido, no sistema de eixos dielétricos, pela equação (12) que aqui se reescreve:

\(\frac{\eta_{1}^{2}}{\varepsilon _1}+\frac{\eta_{2}^{2}}{\varepsilon _2}+\frac{\eta_{3}^{2}}{\varepsilon _3}=\sum_{i=1}^{3}\frac{\eta_{i}^{2}}{\varepsilon _i}=1\) (29)

Seja \(\vec{u}\) o versor da direção de propagação de uma onda eletromagnética. O plano normal a \(\vec{u}\) passando pelo centro do elipsoide, é dado por:

\(\vec{\eta}\cdot\vec{u}=\sum_{i=1}^{3}\eta_iu_i=0\) (30)

O plano intersecta o elipsoide segundo uma elipse cujos semi-eixos são determinados pelos extremos da distância à origem, i.e., pelos máximos e mínimos de:

\(\vec{\eta}^2=\sum_{i=1}^{3}\eta_{i}^{2}\) (31)

sujeitos às condições (29) e (30). Usando o método dos multiplicadores de Lagrange, procurarse- ão os extremos de:

\(\sum_{i=1}^{3}\eta_{i}^{2}-\alpha\left ( \sum_{i=1}^{3}\frac{\eta_{i}^{2}}{\varepsilon _i}-1 \right )-2\beta\sum_{i=1}^{3}\eta_iu_i\)

onde \(\alpha\) e \(\beta\) são os multiplicadores. Derivando, encontra-se:

\(\eta_i\left ( 1-\frac{\alpha}{\varepsilon _i} \right )-\beta u_i=0\) (32)

Multiplicando por \(\eta_i\) e somando sobre \(i = 1, 2, 3\), obtém-se:

\(\sum_{i=1}^{3}\eta_{i}^{2}-\alpha\sum_{i=1}^{\eta_{i}^{2}}\frac{\eta_{i}^{2}}{\varepsilon _i}=0\; \; \; \; \; \rightarrow \; \; \; \; \; \alpha=\sum_{i=1}^{3}\eta_{i}^{2}=\eta^2\)

onde se invocou a equação (30). Assim, a equação (32) reescreve-se:

\(\eta_i=\frac{\beta u_i}{1-\frac{\eta^2}{\varepsilon _i}}=\frac{\beta}{\eta^2}\frac{u_i}{\frac{1}{\eta^2}-\frac{1}{\varepsilon _i}}\) (33)

Multiplicando por \(u_i\), somando sobre \(i\) e atendendo à equação (30), obtém-se:

\(\sum_{i=1}^{3}\frac{u_{i}^{2}}{\frac{1}{\eta^2}-\frac{1}{\varepsilon _i}}=0\)

que é a equação de Fresnel, equação (11), i.e., as soluções \(\eta_a\) e \(\eta_b\) desta equação são os índices de refração das duas ondas propagando-se na direção de \(\vec{u}\). Usando a equação (33), tem-se:

\(\eta_{i}^{\left ( a \right )}\propto \frac{u_i}{\frac{1}{\eta_{a}^{2}}-\frac{1}{\varepsilon _i}}\; \; \; \; \; \; \; \; \; \; \eta_{i}^{\left ( b \right )}\propto \frac{u_i}{\frac{1}{\eta_{b}^{2}}-\frac{1}{\varepsilon _i}}\) (34)

São, então, estas as direções dos máximo e mínimo da distância à origem. Os dois vetores \(\vec{\eta}^{\left ( a \right )}\) e \(\vec{\eta}^{\left ( b \right )}\) são ortogonais, o que confirma serem os semi-exos da elipse resultante da interseção:

\(\vec{\eta}^{\left ( a \right )}\cdot \vec{\eta}^{\left ( b \right )} \propto \sum_{i=1}^{3}\frac{u_{i}^{2}}{\left ( \frac{1}{\eta_{b}^{2}}-\frac{1}{\varepsilon _i} \right )\left ( \frac{1}{\eta_{b}^{2}-\frac{1}{\varepsilon _i}} \right )}\propto \sum_{i=1}^{3}u_{i}^{2}\left ( \frac{1}{\frac{1}{\eta_{a}^{2}}-\frac{1}{\varepsilon _i}}-\frac{1}{\frac{1}{\eta_{b}^{2}}-\frac{1}{\varepsilon _i}} \right )=0\)

como decorre da equação de Fresnel. Estas mesmas direções são as direções da polarização \(\vec{D}\) das duas ondas. Com efeito, a equação (5) reescreve-se:

\(\eta^2E_i-\left ( \bar{u}\cdot\vec{E} \right )\eta^2u_i=D_i=\varepsilon _iE_i\; \; \; \; \; \rightarrow \; \; \; \; \; E_i=\bar{u}\cdot\vec{E}\frac{u_i}{1-\frac{\varepsilon _i}{\eta^2}}\)

Então:

\(D_i=\varepsilon _iE_i\propto \frac{u_i}{\frac{1}{\varepsilon _i}-\frac{1}{\eta^2}}\; \; \; \; \; \rightarrow \; \; \; \; \; \vec{D}^{\left ( a \right )}\left | \right |\vec{\eta}^{\left ( a \right )}\vec{D}^{\left ( b \right )}\left | \right |\vec{\eta}^{\left ( b \right )}\)

como resulta por comparação da equação anterior com a equação (34).

Notas

^a Soma sobre índice repetido.

^b Basta multiplicar ambos os membros da equação pela matriz, o que conduz à mesma equação mas com \(\binom{E_x}{E_y}\rightarrow \binom{D_x}{D_y}\).

^c É mais fácil obter estas equações fazendo \(k_2 = 0\) no anulamento do determinante da eq. (6), completando, depois, os resultados atendendo à simetria de revolução.