Essa representação proposta por Pedro Nunes nessa obra de 1566, foi efetuada em 1569 pela primeira vez num Mapa-mundi por Gerardus Mercator, e viria a ser a projeção cilíndrica conforme, ainda hoje a mais utilizada nas cartas de marear³.

No artigo anterior⁴, descreveu-se como, através da aplicação interativa LOXODRÓMIAS E ESPIRAIS (), loxo, se podem traçar virtualmente linhas de rumo na superfície esférica da Terra, escolhendo um azimute partindo de Lisboa ou comparando as rotas entre duas cidades, escolhidas numa lista, ou entre dois quaisquer pontos no globo a partir das suas latitudes e longitudes. Descreve-se agora como também se podem relacionar essas espirais esféricas com algumas das suas projeções planas, que ainda sendo espirais, permitem a esclarecer o enigma das curvas da roseta de Pedro Nunes incluída no seu Tratado publicado em Lisboa em 1537. A primeira representação de Nunes é uma simples projeção ortográfica do equador numa ilustração já referida anteriormente³. A segunda é a roseta de Nunes, representada na Figura 1, que motivou a segunda componente da loxo que ilustra, de forma interativa, algumas variantes de projeções planas duma linha de rumo, partindo do facto, conhecido desde o século XVII, que a sua projeção estereográfica é uma espiral logarítmica que interseta as linhas radiais num plano segundo ângulos iguais, tal como a loxodrómia interseta os meridianos da esfera sempre segundo o mesmo ângulo.

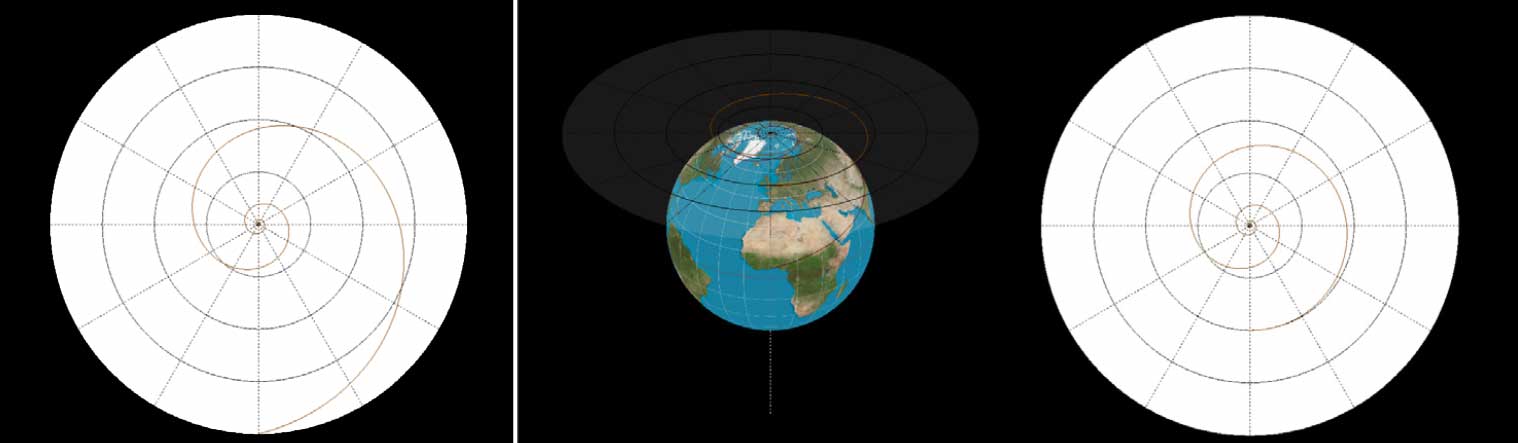
A projeção estereográfica, conhecida no tempo de Ptolemeu e dos matemáticos da antiguidade como projeção planisférica, projeta a superfície esférica a partir de um dos polos no plano tangente ao polo oposto^{5, 6}. Esta projeção preserva os ângulos, i.e., é conforme, mas não mantém nem as distâncias entre pontos nem as áreas. A Figura 2 mostra um plano tangente à esfera da Terra no polo Norte reproduzindo, à esquerda, a espiral logarítmica que se obtém com a projeção estereográfica de uma loxodrómia correspondente a um azimute de 76° e que traduziria sua meia sombra nesse plano se se colocasse um foco de luz exatamente no polo Sul. Na loxo, um ponto-cursor faz mover a perspetiva de forma contínua a partir do polo Sul até ao infinito, deformando no plano a espiral logarítmica até se obter uma espiral de Poinsot⁶, que está representada no círculo branco da direita na Figura 2 e traduz a meia sombra da loxodrómia quando a luz é paralela ao eixo da Terra. A espiral de Poinsot corresponde à projeção ortográfica da loxodrómia e mostra a Terra tal como aparece vista do espaço exterior à medida que o observador se afasta dela. As duas espirais, apesar de parecidas, correspondem a equações diferentes que se podem obter uma da outra com a variação contínua de um parâmetro, e o ponto-cursor da loxo permite deformar a espiral logarítmica numa espiral de Poinsot.

A imagem que ilustra o menu da loxo reproduz uma roseta com que Pedro Nunes, no seu tratado de 1537, pretendeu ilustrar loxodrómias com azimutes de 45° e 67,5°. Sobre esta representação, na Figura 3 estão representadas as projeções de loxodrómias com espirais intermédias obtidas com a mudança do ponto de perspetiva que transforma a espiral logarítmica na espiral de Poinsot e permite aproximar essas espirais às curvas da roseta de Pedro Nunes, iluminando um enigma que perdurava.

De facto, pode ser verificado com a loxo que não existe nenhum ponto de perspetiva que corresponda aos arcos da roseta de Pedro Nunes, pois também foi verificado, com outros meios, que estes correspondem a arcos de circunferência justapostos.

A versão interativa da loxo, inicialmente criada em dezembro de 2012, foi integrada, no ano seguinte dedicado à Matemática do Planeta Terra, na Exposição “Formas e Fórmulas”, que esteve em exibição no Museu da Universidade de Lisboa, entre junho de 2012 e julho de 2016. A atual versão está livremente disponível em http://formas-formulas.fc.ul.pt/interactive/loxo/pt/index_pt.html.

Consulte a primeira parte do artigo em rce.casadasciencias.org/art/2017/022