Neste trabalho são apresentadas as definições de gradiente, divergência e rotacional e são deduzidas as propriedades mais importantes destas operações. No que se segue, consideramos um sistema triretangular de eixos cartesianos onde se definem as coordenadas \(\left ( x_{1},x_{2},x_{3} \right )\) e os versores \(\vec{e_{1}}\), \(\vec{e_{2}}\), \(\vec{e_{3}}\) associados, formando uma base ortonormada e direta. Esta notação mais simétrica tem grandes vantagens em relação à mais habitual notação \(\left ( x,y,z \right )\), mas é totalmente equivalente.

Gradiente

Esta operação generaliza a noção de derivada a funções definidas no espaço tridimensional. Designemos por \(f\left ( x_{1},x_{2},x_{3} \right )\) um campo¹ escalar de que são exemplos os campos de temperatura, pressão, potencial elétrico, etc.. Partindo de um ponto \(P\) de coordenadas \((x_{1},x_{2},x_{3})\), consideramos um pequeno passo \(\delta \vec{r}=\left ( \delta x_{1},\delta x_{2},\delta x_{3} \right )\) que nos leva a um outro ponto \(Q\) que tem, pois, coordenadas \(\left ( x_{1}+\delta x_{1},x_{2}+\delta x_{2},x_{3}+\delta x_{3} \right )\) (FIGURA 1). O gradiente da função, em \(P\), que notamos por \(gradf\), é um vetor definido por:

\(gradf\cdot \delta \vec{r}=f\left ( x_{1}+\delta x_{1},x_{2}+\delta x_{2},x_{3}+\delta x_{3} \right )-f\left ( x_{1},x_{2},x_{3} \right )\) (1)

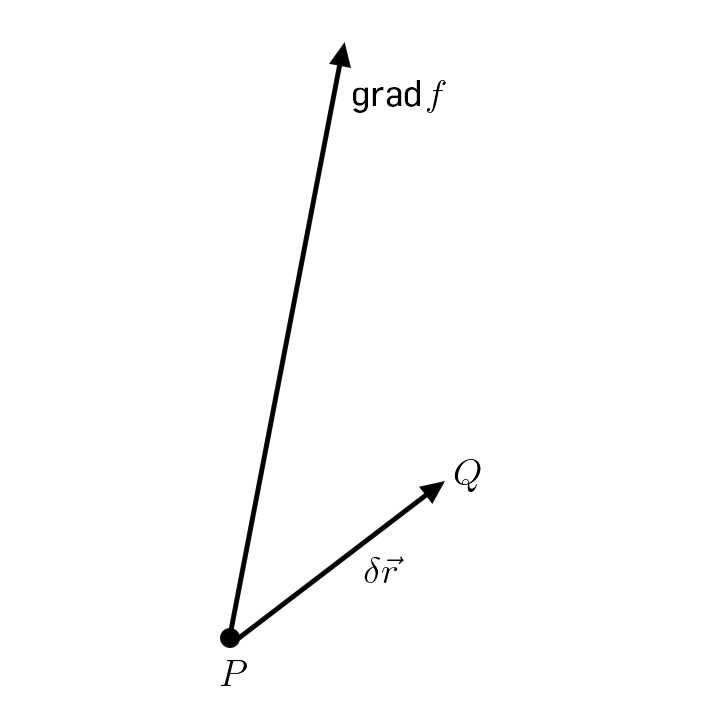
Facilmente encontramos as componentes cartesianas deste vetor. Com efeito, para um passo apenas na direção \(x_{1}\) i.e., \(\delta \vec{r}=\vec{e}_{1}\delta x_{1}\), obtemos, pela equação anterior:

\(\left ( gradf \right )_{x_{1}}\delta x_{1}=f\left ( x_{1}+\delta x_{1},x_{2},x_{3} \right )-f\left ( x_{1},x_{2},x_{3} \right )=\frac{\partial f}{\partial x_{1}}\delta x_{1}\)

Assim:

\(\left ( gradf \right )_{x_{1}}=\frac{\partial f}{\partial x_{1}}\)

Do mesmo modo se obtêm as outras componentes. Então:

\(gradf=\vec{e}_{1}\frac{\partial f}{\partial x_{1}}+\vec{e}_{2}\frac{\partial f}{\partial x_{2}}+\vec{e}_{3}\frac{\partial f}{\partial x_{3}}\) (2)

Algumas importantes propriedades do gradiente decorrem da sua definição. Assim:

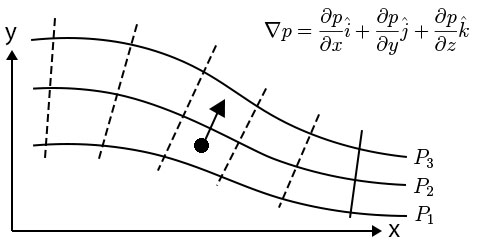
a) Consideremos a superfície \(f\left ( x_{1},x_{2},x_{3} \right )=C=\) constante, passando por \(P\). Partindo deste ponto e para qualquer passo infinitesimal \(\delta \vec{r}\) tangente à superfície, o ponto final \(Q\) também se situa na superfície pelo que o valor da função é o mesmo. É, pois, nulo o 2º membro da eq. (1); então, o 1º membro da mesma equação, sendo nulo, significa que \(gradf\) é normal à superfície (ou é nulo). A FIGURA 2 exibe esta propriedade para um campo de pressões, onde \(p_{1}\)\(<\)\(p_{2}\)\(<\)\(p_{3}\).

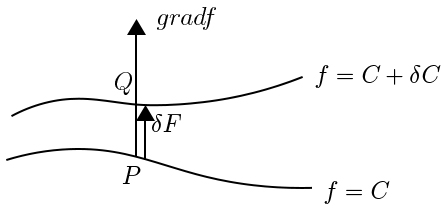
b) Imaginemos, agora, uma outra superfície muito próxima da anterior, definida por \(f\left ( x_{1},x_{2},x_{3} \right )=C+\delta C\), com \(\delta C>0\). As duas superfícies obviamente não se intersetam. A perpendicular à primeira superfície em \(P\) intersecta a segunda superfície num ponto \(Q\) (FIGURA 3). Usando \(\delta \vec{r}=\overrightarrow{PQ}\) na eq. (1), resulta \(gradf\cdot \delta \vec{r}=\delta C\). Mas quer \(\delta \vec{r}\), quer \(gradf\) são normais à superfície e como \(\delta C>0\), segue-se que aqueles vetores têm o mesmo sentido. Obtemos, assim, a distância entre as duas superfícies, medida a partir de \(P\): \(\left | \delta \vec{r} \right |=\frac{\delta C}{\left | gradf \right |}\). Esta relação é muitas vezes usada para determinar a distância entre duas superfícies muito próximas.

c) Na eq. (2), a função \(f\) é qualquer, o que nos leva a definir o operador nabla \(\left ( {\nabla} \right )\) em coordenadas cartesianas:

\(\nabla =\sum_{i-1}^{3}\vec{e}_{i}\frac{\partial }{\partial x_{i}}\) (3)

Aplicando nabla qualquer função, obtemos o seu gradiente:

\(\nabla f=gradf\) (4)

d) Em coordenadas cilíndricas (FIGURA 4), a posição do mesmo ponto \(P\) é especificada por:

\(r\) - a distância ao eixo \(x_{3}\)

\(\phi \) - azimute, ângulo do plano \(x_{1}x_{3}\) com o plano contendo \(p\) e o eixo \(x_{3}\)

\(z\) - cota, coincidente com \(x_{3}\)

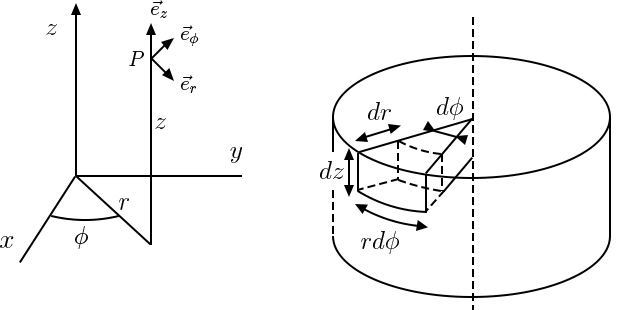
Associamos ao ponto \(P\) uma base local, ortonormado, definida pelos versores:

\(\vec{e}_{r}\) - perpendicular ao eixo \(x_{3}\), com o sentido do crescimento de \(r\)

\(\vec{e}_{\phi }\) - perpendicular ao plano definido por \(P\) e o eixo \(x_{3}\), com o sentido do crescimento de \(\phi \)

\(\vec{e}_{z}\) - versor do eixo \(z\), com o sentido do crescimento de \(z\)

A relação destas coordenadas com as coordenadas cartesianas encontra-se sem dificuldade:

\(\begin{matrix} x_{1}=rcos\phi & &\vec{e}_{r}=cos\phi \vec{e}_{1}+sen\phi \vec{e_{2}} \\ x_{2}=rsen\phi & &\vec{e}_{r}=-sen\phi \vec{e}_{1}+cos\phi \vec{e}_{2} \\ x_{3}=z & & \vec{e}_{z}=\vec{e}_{3} \end{matrix}\)

Um passo infinitesimal \(\delta \vec{r}\) tem componentes que se deduzem da FIGURA 4:

\(\delta \vec{r}=\delta r\vec{e}_{r}+r\delta \phi \vec{e}_{\phi }+\delta z\vec{e}_{z}\)

Os três termos no segundo membro definem um “paralelepípedo” curvo, representado na mesma figura, de onde se obtém o elemento de volume em coordenadas cilíndricas:

\(dV=drrd\phi dz\) (5)

Usando a eq. (1) adaptada às novas coordenadas, tem-se:

\(gradf\cdot \delta \vec{r}=f\left ( r+\delta r,\phi +\delta \phi ,z+\delta z \right )-f\left ( r,\phi ,z \right )\)

Procedendo como antes, obtemos:

\(gradf=\vec{e}_{r}\frac{\partial f}{\partial r}+\vec{e}_{\phi }\frac{1}{r}\frac{\partial f}{\partial \phi }+\vec{e}_{z}\frac{\partial f}{\partial z}\) (6)

Donde resulta a expressão do operador nabla em coordenadas cilíndricas:

\(\nabla f=\vec{e}_{r}\frac{\partial }{\partial r}+\vec{e}_{\phi }\frac{1}{r}\frac{\partial }{\partial \phi }+\vec{e}_{z}\frac{\partial }{\partial z}\) (7)

Deve, aqui, notar-se que as derivadas são aplicadas antes dos versores, para evitar confusões: alguns versores dependem, também, das coordenadas.

e) Em coordenadas esféricas (FIGURA 5), a posição do mesmo ponto \(P\) é definida por:

\(r\) - distância à origem

\(\theta \) - co-latitude, ângulo de abertura do cone, com eixo \(x_{3}\) e contendo \(P\)

\(\phi \) - longitude, ângulo do plano \(x_{1}x_{3}\) com o plano contendo \(P\) e o eixo \(x_{3}\)

Associado ao ponto \(P\), definimos uma base local, ortonormada, com versores (FIGURA 5):

\(\vec{e}_{r}\) - com a direção da semi-reta que une a origem a \(P\) e sentido do crescimento de \(r\)

\(\vec{e}_{\theta }\) - tangente ao meridiano passado por \(P\) e sentido do crescimento de \(\theta \)

\(\vec{e}_{\phi }\) - tangente ao paralelo passando por \(P\) e sentido do crescimento de \(\phi \)

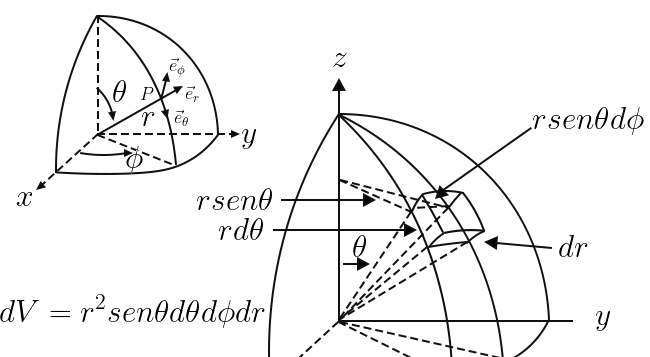
A relação destas coordenadas com as cartesianas obtem-se da FIGURA 3:

\(\begin{matrix} x_{1}=rsen\theta cos\phi & &\vec{e}_{r}=sen\theta cos\phi \vec{e}_{1}+sen\theta sen\phi \vec{e}_{2}+cos\theta \vec{e}_{3} \\ x_{2}=rsen\theta cos\phi & &\vec{e}_{\theta}=cos\theta cos\phi \vec{e}_{1}+cos\theta sen\phi \vec{e}_{2}-sen\theta \vec{e}_{3} \\ x_{3}=rcos\theta & & \vec{e}_{\theta}=-sen\theta \phi \vec{e}_{1}+cos\phi \vec{e}_{2} \end{matrix}\)

Um passo infinitesimal \(\delta \vec{r}\) com origem em \(P\) tem componentes:

\(\delta \vec{r}=\delta r\vec{e}_{r}+r\delta \theta \vec{e}_{\theta }+rsen\theta \delta \phi \vec{e}_{\phi }\)

Assim, usando a eq. (1) adaptada às coordenadas esféricas:

\(gradf\cdot \delta \vec{r}=f\left ( r+\delta r,\theta +\delta \theta ,\phi +\delta \phi \right )-f\left ( r,\theta ,\phi \right )\)

obtemos, procedendo como antes:

\(gradf=\vec{e}_{r}\frac{\partial f}{\partial r}+\vec{e}_{\theta }\frac{1}{r}\frac{\partial f}{\partial \theta }+\vec{e}_{\phi }\frac{1}{rsen\theta }\frac{\partial }{\partial \phi }\) (8)

Daqui deduzimos a expressão do operador nabla em coordenadas esféricas:

\(\nabla=\vec{e}_{r}\frac{\partial }{\partial r}+\vec{e}_{\theta }\frac{1}{r}\frac{\partial }{\partial \theta }+\vec{e}_{\phi }\frac{1}{rsen\theta }\frac{\partial }{\partial \phi }\) (9)

Deve, de novo, ser realçado que as derivadas são aplicadas antes dos versores, para evitar confusões: alguns versores dependem, também, das coordenadas.

Divergência

Começamos por recordar, sem demonstração, o teorema de Gauss na sua forma mais geral. Consideremos um domínio \(D\) limitado por uma superfície fechada \(\Sigma \), em cada ponto da qual se pode definir o vetor unitário da normal \(\vec{n}\) dirigido para o exterior do domínio. Seja \(f\left ( x_{1},x_{2},x_{3} \right )\) uma qualquer função, contínua e derivável, definida no domínio e na superfície.

O teorema de Gauss estabelece a seguinte identidade:

\(\begin{matrix} \int_{D}^{}dV\frac{\partial f}{\partial _{x_{k}}}=\int_{\Sigma }^{}dSfn_{k} & & k=1,2,3 \end{matrix}\) (10)

Trata-se, pois, de uma generalização da conhecida integração por partes. Como a função é arbitrária, identifiquemo-la com a componente \(u_{j}\left ( x_{1},x_{2},x_{3} \right )\) de um campo vetorial; tem-se:

\(\begin{matrix} \int_{D}^{}dV\frac{\partial u_{j}}{\partial _{x_{k}}} & & j,k=1,2,3 \end{matrix}\) (11)

Como caso particular, façamos \(k=j\) e somemos sobre \(k\), obtendo-se:

\(\int_{D}^{}dVdiv\vec{u}=\int_{\Sigma }^{}dS\vec{n}\cdot \vec{u}\) (12)

onde:

\(div\vec{u}=\sum_{k-1}^{3}\frac{\partial _{u_{k}}}{\partial _{x_{k}}}= \nabla \cdot \vec{u}\) (13)

é, por definição, a divergência do campo vetorial \(\vec{u}\) nas coordenadas cartesianas aqui usadas. A última expressão acima faz uso do operador nabla naquelas coordenadas (ver eq. (3)). O segundo membro na eq. (12) é o fluxo de \(\vec{u}\) através da superfície \(\Sigma \). Divergência e fluxo estão, pois, relacionados, como bem se percebe na FIGURA 6; ambos são de grande importância em Física, recordando-se, aqui, como exemplos, o fluxo não nulo de um campo elétrico relacionado com a presença de cargas no interior do domínio, o fluxo sempre nulo do campo magnético, para qualquer superfície fechada, indicando que não existem cargas magnéticas, ou o fluxo de massa através da superfície que se relaciona com a diminuição de massa, na unidade de tempo, no interior do domínio, originando a equação da continuidade em fluidos.

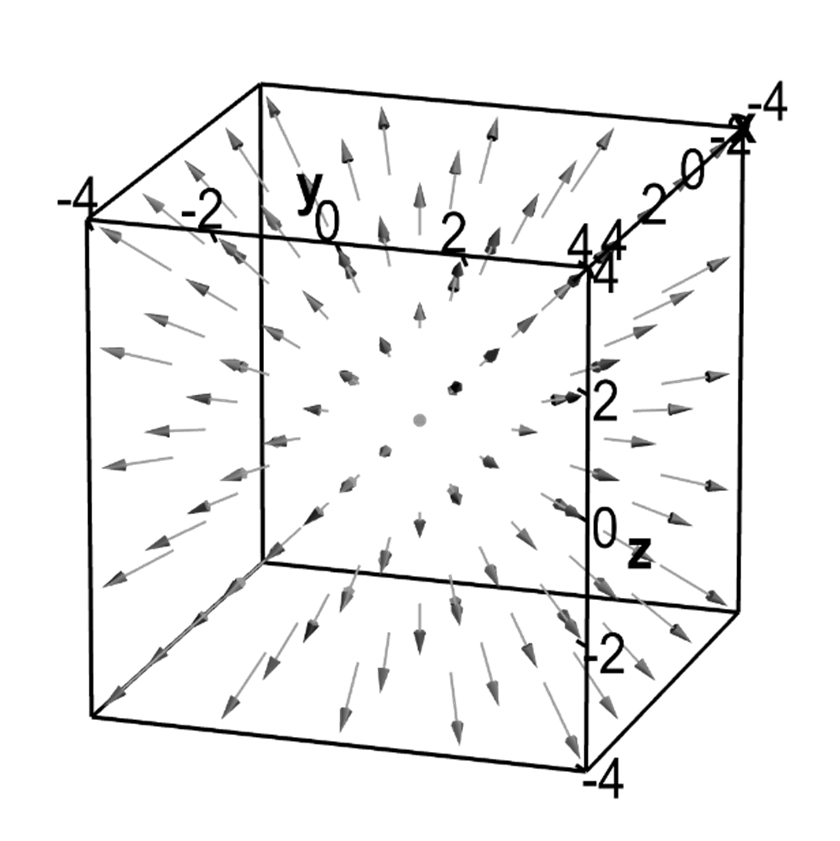
Usaremos, agora, a eq. (12) para obter a expressão da divergência nas coordenadas curvilíneas já atrás definidas.

a) Coordenadas cilíndricas

Consideremos o ponto \(P\) de coordenadas \(r\), \(\phi \), \(z\) que será o centro do “paralelepípedo” infinitesimal representado na FIGURA 4. Na tabela abaixo, identificamos cada face pelo valor da coordenada que nela permanece fixa, o respectivo versor da normal (exterior), a sua área e a contribuição para o fluxo:

Somando os fluxos, obtemos o segundo membro da eq. (12):

fluxo\(=\left [ \frac{\partial }{\partial r}\left ( ru_{r} \right )+\frac{\partial u_{\phi }}{\partial \phi }+r\frac{\partial u_{z}}{\partial z} \right ]drd\phi dz\)

O volume do paralelepípedo é:

\(dV=rdrd\phi dz\) (14)

Usando a eq. (12), obtemos a expressão da divergência em coordenadas cilíndricas:

\(div\vec{u}=\frac{1}{r}\frac{\partial }{\partial r}\left ( ru_{r} \right )+\frac{1}{r}\frac{\partial u_{\phi }}{\partial \phi }+\frac{\partial u_{\phi }}{\partial z}\) (15)

b) Coordenadas esféricas

Consideremos o ponto \(P\) de coordenadas \(r\), \(\theta \), \(\phi \) que será o centro do paralelepípedo infinitesimal representado na FIGURA 5 Na tabela abaixo, identificamos cada face pelo valor da coordenada que nela permanece fixa, o respetivo versor da normal (exterior), a sua área e a contribuição para o fluxo:

Somando os fluxos, obtemos o segundo membro da eq. (12):

fluxo\(=\left [ \left ( \frac{\partial \left ( r^{2}u_{r} \right )}{\partial r} \right )sen\theta +r\frac{\partial \left ( sen\theta u_{\phi } \right )}{\partial \theta }+r\frac{\partial u_{\phi }}{\partial \phi } \right ]drd\theta d\phi \)

O volume do paralelepípedo é:

\(dV=r^{2}sen\theta drd\theta d\phi \) (16)

Usando a eq. (12), obtemos a expressão da divergência em coordenadas esféricas:

\(div\vec{u}=\frac{1}{r^{2}}\frac{\partial }{\partial r}\left ( r^{2}u_{r} \right )+\frac{1}{rsen\theta }\frac{\partial }{\partial \theta }\left ( sen\theta u_{\theta } \right )+\frac{1}{rsen\theta }\frac{\partial }{\partial \phi }u_{\phi }\) (17)

c) O laplaciano de uma função é a divergência do seu gradiente. Este importante operador intervém na equação de Poisson em eletromagnetismo, nas equações de propagação de ondas, na mecânica quântica, etc.. As suas expressões nos três sistemas de coordenadas que vimos considerando, obtêm-se diretamente dos resultados anteriores:

\(\Delta f=\frac{\partial ^{2}f}{\partial x_{1}^{2}}+\frac{\partial ^{2}f}{\partial x_{2}^{2}}+\frac{\partial ^{2}f}{\partial x_{3}^{2}}\) coordenadas cartesianas

\(\Delta f=\frac{1}{r}\frac{\partial }{\partial r}\left ( r\frac{\partial f}{\partial r} \right )+\frac{1}{r^{2}}\frac{\partial ^{2}f}{\partial \phi ^{2}}\frac{\partial ^{2}f}{\partial z^{2}}\) coordenadas cilíndricas (18)

\(\Delta f=\frac{1}{r^{2}}\frac{\partial }{\partial r}\left ( r^{2}\frac{\partial f}{\partial r} \right )+\frac{1}{r^{2}sen\theta }\frac{\partial }{\partial \theta }\left ( sen\theta\frac{\partial f}{\partial \theta } \right )+\frac{1}{r^{2}sen^{2}\theta }\frac{\partial ^{2}f}{\partial \phi ^{2}}\) coordenadas esféricas

Rotacional

O rotacional de um campo vetorial é outro importante conceito que está associado com a circulação do vetor ao longo de uma linha fechada. A associação é estabelecida pelo teorema de Stokes, aqui recordado sem demonstração.

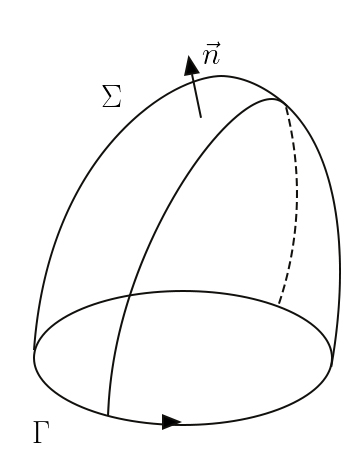
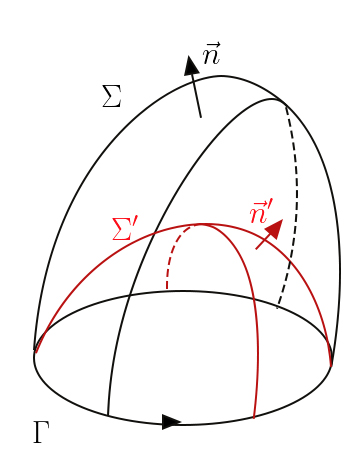
Consideremos uma linha fechada \(\Gamma \) onde arbitramos um sentido de circulação; seja \(\Sigma \) uma superfície aberta que se apoia nessa linha. Em cada ponto da superfície definimos o versor da normal, \(\vec{n}\), com um sentido determinado pelo sentido da circulação pela regra do saca-rolhas (FIGURA 7). O teorema de Stokes afirma:

\(\oint_{\Gamma }^{}d\vec{l}\cdot \vec{u}=\int_{\Sigma }^{}dS\vec{n}\cdot rot\vec{u}\)

Aqui, o primeiro membro é a circulação, ao longo da linha, do campo vetorial \(\vec{u}\), sendo \(d\vec{l}\) um vetor infinitesimal com o sentido escolhido para a circulação e grandeza igual ao elemento de comprimento. Quanto ao segundo membro, ele será aqui considerado como definindo o rotacional do campo de vetores. Mostraremos adiante que a escolha da superfície \(\Sigma \) é irrelevante: qualquer uma serve desde que se apoie na linha.

O rotacional intervém em vários domínios da Física: na lei de Faraday-Maxwell traduzindo a indução eletromagnética ou na dinâmica de fluidos (FIGURA 8) onde descreve movimentos turbilhonares. Está associado com a ideia de uma rotação do campo que, em geral, é não uniforme.

Começaremos por mostrar a identidade:

\(div\left ( rot\vec{u} \right )=0\) (20)

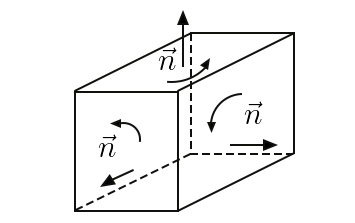
Para isso, consideramos um pequeno paralelepípedo centrado no ponto \(P\) . Usando o teorema de Gauss, tem-se:

\(\int dVdiv\left ( rot\vec{u} \right )=\int dS\vec{n}\cdot rot\vec{u}\)

No primeiro membro, o integral tem por domínio o interior do paralelepípedo; no segundo membro, o integral estende-se às seis faces que limitam o domínio e, em cada uma delas, o versor da normal aponta para o exterior do domínio (FIGURA 9). Ora, pela eq. (19), o fluxo do rotacional em cada face converte-se na circulação do campo ao longo dos lados do retângulo que limita a face, com o sentido da circulação determinado pelo sentido da normal. Deste modo, em cada aresta do paralelepípedo, a circulação faz-se em sentidos opostos para as duas faces que partilham a aresta, anulando-se mutuamente. Assim, é nulo o segundo membro da equação anterior, sendo, então, nulo o primeiro membro. Como o paralelepípedo é arbitrário, este anulamento implica o resultado que se pretendia mostrar.

Imagine-se, agora, uma outra superfície aberta \(\Sigma '\) que se apoie sobre a mesma linha fechada \(\Gamma \), em cada ponto da qual o versor da normal \(\vec{n}'\) tem o sentido estabelecido pela circulação escolhida na linha (FIGURA 10). As duas superfícies limitam um domínio fechado. Usando o teorema de Gauss com \(div\left ( rot\vec{u} \right )=0\), concluímos que o fluxo de \(rot\vec{u}\) para o exterior daquelas superfícies. Mas se, por exemplo, o versor \(\vec{n}\) é exterior ao domínio na superfície \(\Sigma \), então é \(-\vec{n}'\) o versor exterior para a superfície \(\Sigma '\), isto é:

\(\int_{\Sigma }^{}dS\vec{n}\cdot rot\vec{u}+\int_{\Sigma '}^{}dS'\left ( -\vec{n} \right )\cdot rot\vec{u}=0\)

Assim, o fluxo do rotacional através das duas superfícies é o mesmo, pelo que a escolha da superfície que se apoia em \(\Gamma \) eq. (19) é irrelevante.

Regressando à eq. (19), consideremos o caso particular \(\vec{u}=gradf\). O primeiro membro daquela equação fica: \(\oint_{\Gamma }^{}d\vec{l}\cdot gradf=0\) porque a função regressa ao seu valor inicial. Então, como a linha é arbitrária, obtemos uma impor tante conclusão:

\(rot\left ( gradf \right )=0\) (21)

a) Coordenadas cartesianas

Imaginemos um retângulo infinitesimal centrado em \(P\) , de coordenadas \(\left ( x_{1},x_{2},x_{3} \right )\) e lados paralelos aos eixos \(x_{1}\) e \(x_{2}\) com dimensões \(\delta x_{1}\) e \(\delta x_{2}\) respectivamente. Escolhamos o sentido de circulação no retângulo de modo que o versor da normal ao seu plano é \(\vec{e}_{3}\). A tabela abaixo indica as contribuições de cada lado para o primeiro membro da eq. (19): a primeira coluna identifica o lado pelo valor da coordenada que permanece fixa e a segunda coluna refere o valor de \(\vec{u}\cdot d\vec{l}\).

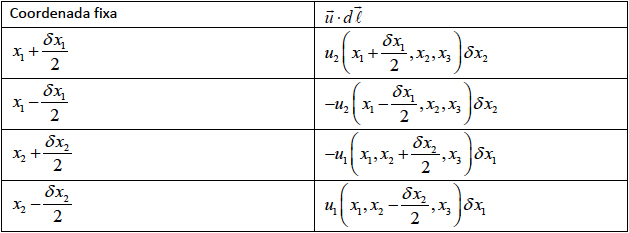
Somando as contribuições, obtemos para o primeiro membro na eq. (19) o resultado:

\(\left ( \frac{\partial u_{2}}{\partial x_{1}}-\frac{\partial u_{1}}{\partial x_{2}} \right )\delta x_{1}\delta x_{2}\)

Quanto ao segundo membro da mesma equação, fica \(\left ( rot\vec{u} \right )_{3}\delta x_{1}\delta x_{2}\). Assim:

\(\left ( rot\vec{u} \right )_{3}=\frac{\partial u_{2}}{\partial x_{1}}-\frac{\partial u_{1}}{\partial x_{2}}\)

Procedendo do mesmo modo para os outros planos coordenados, obtemos as outras componentes cartesianas do rotacional:

\(\begin{matrix} \left ( rot\vec{u}\right )_{1}=\frac{\partial u_{3}}{\partial x_{2}}-\frac{\partial u_{2}}{\partial x_{3}} \\ \left ( rot\vec{u} \right )_{2}=\frac{\partial u_{1}}{\partial x_{3}}-\frac{\partial u_{3}}{\partial x_{1}} \end{matrix}\)

Estes resultados podem ser obtidos desenvolvendo o seguinte determinante segundo a primeira linha:

\(rot\vec{u}=\begin{vmatrix} \vec{e}_{1} & \vec{e}_{2} & \vec{e}_{3}\\ \frac{\partial }{\partial x_{1}} & \frac{\partial }{\partial x_{2}} & \frac{\partial }{\partial x_{3}}\\ u_{1} & u_{2} & u_{3} \end{vmatrix}=\nabla \wedge \vec{u}\) (22)

Aqui, a última expressão resulta da expressão de nabla em coordenadas cartesianas, eq. (3). É imediato verificar as identidades atrás obtidas, eqs. (20) e (21).

É, também, fácil concluir que o rotacional de um campo de vetores é um pseudovetor², notando, por exemplo, que sob inversão de coordenadas quer as componentes de \(\vec{u}\) quer as derivadas em nabla trocam de sinal, pelo que as componentes do rotacional não trocam de sinal.

Um exemplo interessante consiste em considerar o campo de velocidades de um sólido rígido:

\(\vec{v}=\vec{v}_{0}+\vec{\omega }\wedge \vec{r}\)

Aqui, \(\vec{v}_{0}\) é independente das coordenadas, tal como o vetor velocidade de rotação instantânea, \(\vec{\omega }\). Um cálculo simples mostra que \(rot\vec{v}=2\vec{\omega }\), que bem traduz estar o rotacional relacionado com uma rotação.

b) Coordenadas cilíndricas

O mesmo ponto \(P\) tem, agora, coordenadas \(\left ( r,\phi ,z \right )\). Consideramo-lo como centro de três “retângulos” curvos infinitesimais, cada um definido por uma coordenada fixa e as outras sofrendo acréscimos iguais e de sinais contrários às respetivas coordenadas de \(P\). Em cada retângulo o sentido de circulação é determinado de maneira a que o versor da normal ao retângulo coincida com o versor da base local associado com a coordenada fixa. Na tabela abaixo, a 1ª coluna identifica a coordenada fixa, a 2ª coluna indica o versor da normal, a 3ª coluna define cada um dos lados do retângulo pelo valor da outra coordenada constante e a 4ª coluna mostra a contribuição para a circulação do lado considerado.

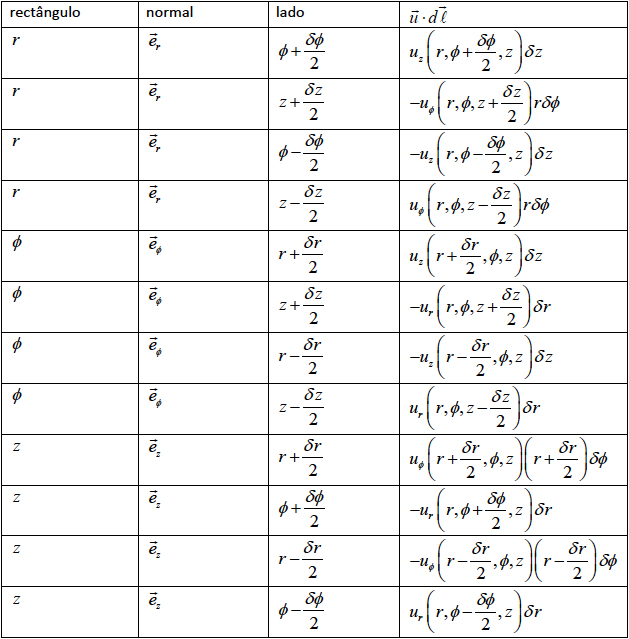
Aplicando, agora, a eq. (19) a cada um dos retângulos, obtemos as componentes cilíndricas do rotacional indicadas na última coluna da seguinte tabela:

Estas três componentes podem ser formalmente obtidas desenvolvendo o seguinte determinante a partir da primeira linha:

\(rot\vec{u}=\frac{1}{r}\begin{vmatrix} \vec{e}_{r} & r\vec{e}_{\phi } & \vec{e}_{z}\\ \frac{\partial }{\partial r} & \frac{\partial }{\partial _{\phi }} & \frac{\partial }{\partial z}\\ u_{r} & ru_{\phi } & u_{z} \end{vmatrix}\) (23)

c) Coordenadas esféricas

O mesmo ponto \(P\) tem, agora, coordenadas \(\left ( r,\theta ,\phi \right )\). Consideramo-lo como centro de três “retângulos” curvos infinitesimais, cada um definido por uma coordenada fixa e as outras sofrendo acréscimos iguais e de sinais contrários às respetivas coordenadas de \(P\). Em cada retângulo o sentido de circulação é determinado de maneira a que o versor da normal ao retângulo coincida com o versor da base local associado com a coordenada fixa. Na tabela abaixo, a 1ª coluna identifica a coordenada fixa, a 2ª coluna indica o versor da normal, a 3ª coluna define cada um dos lados do retângulo pelo valor da outra coordenada constante e a 4ª coluna mostra a contribuição para a circulação do lado considerado.

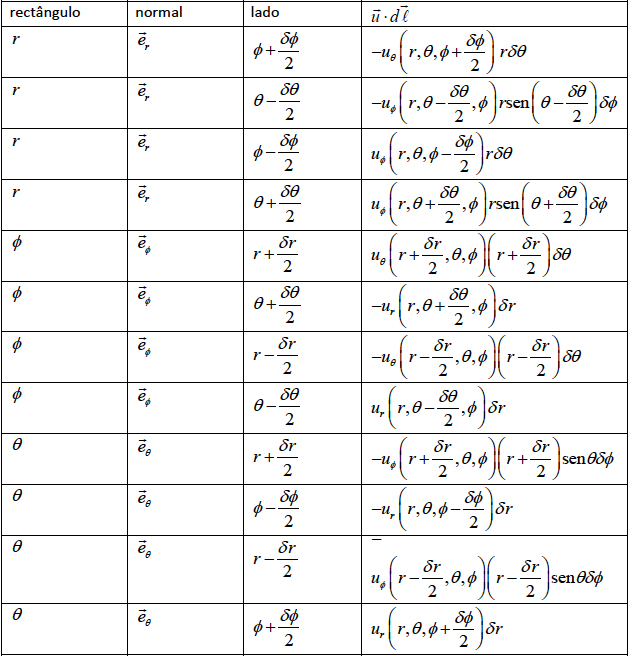
Aplicando, agora, a eq. (19) a cada um dos retângulos, obtemos as componentes esféricas do rotacional indicadas na última coluna da seguinte tabela:

Estas três componentes podem ser formalmente obtidas desenvolvendo o seguinte determinante a partir da primeira linha:

\(rot\vec{u}=\frac{1}{r^{2}sen\theta }\begin{vmatrix} \vec{e}_{r} & r\vec{e}_{\theta } & rsen\theta \vec{e}_{\phi }\\ \frac{\partial }{\partial r} & \frac{\partial }{\partial _{\theta }} & \frac{\partial }{\partial _{\phi }}\\ u_{r} & ru_{\theta } & rsen\theta u_{\phi } \end{vmatrix}\) (24)

d) Laplaciano de um campo vetorial

Por definição, o Laplaciano de um campo vetorial é.

\(\Delta \vec{u}=grad\left ( div\vec{u} \right )-rot\left ( rot\vec{u} \right )\) (25)

Apenas em coordenadas cartesianas esta expressão fica simplificada:

\(\Delta \vec{u}=\sum_{k-1}^{3}\left ( \Delta u_{k} \right )\vec{e}_{k}\) (26)

Nas outras coordenadas, teremos de usar a eq. (25) e os resultados antes obtidos para os operadores nelas intervenientes. Prescindimos de escrever aqui as expressões finais.