Noções básicas

Diremos que um conjunto de partículas é, ou comporta-se como, um sólido rígido se a distância entre qualquer par de partículas for sempre constante sendo, em princípio, conhecida. Para caracterizar a posição genérica do sólido no espaço escolhemos arbitrariamente três partículas não colineares. A posição da primeira partícula é definida por três coordenadas num sistema de eixos cartesianos escolhido como referencial imóvel que designaremos por LAB. A segunda partícula situa-se a uma distância conhecida da primeira, localizando-se, portanto, na superfície de uma esfera; são, assim, necessárias duas coordenadas adicionais para a localizar nesta esfera, tal como latitude e longitude localizam qualquer ponto na superfície da Terra. A terceira partícula situa-se na intersecção de duas esferas, uma centrada na primeira partícula e a outra na segunda. Esta intersecção é uma circunferência e a posição da terceira partícula nesta circunferência exige uma outra coordenada. Uma vez conhecidas as posições destas três partículas, ficam conhecidas as posições de todas as outras. São, assim, necessários seis graus de liberdade para definir a posição genérica do sólido no LAB. Este número diminui se o sólido estiver sujeito a condicionamentos: por exemplo, se uma partícula estiver sempre fixa, o número reduz-se para três, ou se o sólido admitir um eixo fixo no espaço, aquele número reduz-se para quatro.

No que se segue, usaremos o sinal \(\sum \), sem qualquer índice, para indicar soma sobre as partículas do sólido, cada uma com massa \(m\) e designando por \(M =\sum m\) a massa do sólido. A passagem ao contínuo, quando necessária, faz-se simplesmente com a substituição \(m \rightarrow pdV\) e \(\sum \rightarrow \int \) sendo este estendido ao volume ocupado pelo sólido.

\(\vec{R}_{G}=\frac{1}{M}\sum m\vec{R}\) (1)

onde \(\vec{r}\equiv \vec{R}-\vec{R}_{G}\) é o vetor de posição no LAB de cada partícula. Reescrevamos esta equação sob a forma:

\(\sum m\left ( \vec{R}-\vec{R}_{G} \right )\equiv \sum m\vec{r}=0\) (2)

\(\vec{r}\equiv \vec{R}-\vec{R}_{G}\) RG é o vetor de posição de cada partícula do sólido em relação ao CM. Este resultado mostra que o centro de massa move-se solidariamente com as partículas do sólido, embora possa não coincidir com nenhuma delas. A eq. (1) identifica o centro de massa com a média da posição das partículas, cada uma contribuindo com um peso estatístico igual à sua massa.

Movendo-se o sólido no espaço, os vetores de posição \(\vec{R}\left ( t \right )\) dependem do tempo, o mesmo acontecendo, pois, ao centro de massa. A quantidade de movimento do sólido é a soma das quantidades de movimento de cada partícula:

\(\vec{P}=\sum m\frac{d\vec{R}}{dt}\equiv \sum m\vec{V}\)

Então, pela eq. (1), obtemos:

\(\vec{P}=M\vec{V}_{G}\) (3)

O centro de massa comporta-se como um ponto material, com a massa do sólido, sendo a sua quantidade de movimento igual à do sólido. É o movimento do centro de massa que vemos quando observamos um objeto distante, tal como uma estrela.

O referencial centro de massa

Recuperamos aqui muitos dos resultados apresentados em “Força”¹. Assim, começamos por considerar um referencial cartesiano ortonormado rigidamente ligado ao sólido, com origem no centro de massa e que designaremos por referencial CM. Os eixos deste referencial são, para já, escolhidos arbitrariamente; mais adiante, torna-se conveniente uma escolha particular. Sejam \(\vec{e}_{1},\vec{e}_{2},\vec{e}_{3}\) os versores dos seus eixos; estes versores deslocam-se no tempo em relação a LAB, mas a posição de qualquer partícula do sólido tem coordenadas fixas em CM:

\(\vec{r}\left ( t \right )=\sum_{k=1}^{3}x_{k}\vec{e}_{k}\left ( t \right )\)

No LAB, a mesma partícula tem o vetor de posição:

\(\vec{R}\left ( t \right )=\vec{R}_{G}\left ( t \right )+\sum_{k=1}^{3}x_{k}\vec{e}_{k}\left ( t \right )\) (4)

Assim, a velocidade da partícula (no LAB) é:

\(\vec{V}\left ( t \right )=\frac{d\vec{R}}{dt}=\vec{V}_{G}\left ( t \right )+\sum_{k=1}^{3}x_{k}\frac{d}{dt}\vec{e}_{k}\left ( t \right )\)

O último termo representa a rotação do sólido¹:

\(\frac{d}{dt}\vec{e}_{k}\left ( t \right )=\vec{\omega }\left ( t \right )\wedge \vec{e}_{k}\left ( t \right )\)

onde \(\vec{\omega }\left ( t \right )\) é o (pseudo) vetor rotação instantânea: num curto intervalo de tempo \(\delta t\), é:

\(\delta \vec{\Omega }\equiv \vec{\omega }\left ( t \right )\delta t\) (5)

a rotação do ângulo \(\left | \delta \vec{\Omega } \right |\), em torno de um eixo paralelo a \(\delta \vec{\Omega }\), passando pelo centro de massa, e no sentido da rotação de um saca-rolhas que progredisse no sentido de \(\delta \vec{\Omega }\). Deste modo, reescrevemos a velocidade do ponto do sólido:

\(\vec{V}\left ( t \right )=\vec{V}_{G}\left ( t \right )+\sum_{k=1}^{3}x_{k}\vec{\omega }\left ( t \right )\wedge \vec{e}_{k}\left ( t \right )=\vec{V}_{G}\left ( t \right )+\vec{\omega }\left ( t \right )\wedge \vec{r}\left ( t \right )\) (6)

Assim, a velocidade de qualquer ponto do sólido é a composição de uma velocidade de translação (a velocidade do centro de massa) com uma velocidade de rotação em torno do centro de massa (o último termo).

Facilmente obtemos a aceleração do mesmo ponto do sólido:

\(\vec{A}\left ( t \right )=\frac{d\vec{V}}{dt}=\vec{A}_{G}\left ( t \right )+\vec{\omega }\left ( t \right )\wedge \vec{r}\left ( t \right )+\vec{\omega }\left ( t \right )\wedge \left ( \vec{\omega }\left ( t \right )\wedge \vec{r}\left ( t \right ) \right )\) (7)

O último termo é a aceleração centrípeta.

A energia cinética do sólido é a soma das energias cinéticas das suas partículas:

\(K=\sum \frac{1}{2}m\vec{V}^{2}=\frac{1}{2}M\vec{V}_{G}^{2}+\frac{1}{2}\sum m\left ( \vec{\omega }\wedge \vec{r} \right )^{2}\) (8)

O resultado obtém-se lembrando a eq. (2) que simplifica o segundo membro; e mostra a decomposição da energia cinética na soma de uma contribuição de translação – o primeiro termo, com uma contribuição de rotação – o segundo termo.

O momento cinético com pólo na origem de LAB é a soma dos momentos cinéticos das partículas do sólido:

\(\vec{L}_{O}=\sum \vec{R}\wedge \left ( m\vec{V} \right )=\sum \vec{R}\wedge \left ( m\vec{V}_{G} \right )+\sum m\vec{R}\wedge \left ( \vec{\omega } \right )\wedge \vec{r}\)

Ora:

\(\sum \vec{R}\wedge \left ( m\vec{V}_{G} \right )=\sum m\left ( \vec{R}_{G}+\vec{r} \right )\wedge \vec{V}_{G}=\vec{R}_{G}\wedge \left ( M\vec{V}_{G} \right )=\vec{R}_{G}\wedge \vec{P}\)

onde, mais uma vez, se usou a eq. (2) para simplificar o resultado final. Esta parcela é conhecida por momento cinético orbital. Quanto à outra parcela, designada por momento cinético intrínseco ou de rotação, tem-se:

\(\sum m\vec{R}\wedge \left ( \vec{\omega }\wedge \vec{r} \right )=\sum m\left ( \vec{R}_{G}+\vec{r} \right )\wedge \left ( \vec{\omega }\wedge \vec{r} \right )=\sum m\vec{r}\wedge \left ( \vec{\omega }\wedge \vec{r} \right )\)

Notar-se-á que este é o momento cinético com pólo no centro de massa.

Os resultados anteriores levam finalmente à expressão:

\(\vec{L}_{O}=\vec{R}_{G}\wedge \vec{P}+\sum m\vec{r}\wedge \left ( \vec{\omega }\wedge \vec{r} \right )\) (9)

Com:

\(\vec{L}_{G}=\sum m\vec{r}\wedge \left ( \vec{\omega }\wedge \vec{r} \right )\) (10)

Aqui reconhece-se, de novo, a decomposição do momento cinético numa parte orbital e numa parte de rotação \(\left ( \vec{L}_{G} \right )\).

É importante notar que as decomposições nas eqs. (8) e (9) só foram possíveis porque usámos o referencial CM; tivéssemos escolhido outra origem para o referencial no sólido, iriam surgir, em geral, termos adicionais.

Momentos de inércia

As contribuições da rotação nas eqs. (8) e (9) têm somas, sobre as partículas, de produtos de pares das coordenadas, no CM, de cada partícula. Explicitemos essas expressões onde, a seguir, os índices se referem a essas coordenadas e um índice repetido implica soma sobre o seu valor (i.e., 1,2,3):

\(\frac{1}{2}\sum m\left ( \vec{\omega }\wedge \vec{r} \right )^{2}=\frac{1}{2}\omega _{i}\omega _{j}\sum m\left ( \vec{r}^{2}\delta _{ij}-x_{i}x_{j} \right )\)

E, para a componente \(i=1,2,3\) do momento cinético de rotação:

\(\omega _{i}\sum m\vec{r}^{2}-\omega _{j}\sum mx_{i}x_{j}=\omega _{j}\sum m\left ( \vec{r}^{2}\delta _{ij}-x_{i}x_{j} \right )\)

onde \(\delta _{ij}\) é o símbolo de Kronecker: \(\delta _{ij}=1\) se \(i=j\) e \(\delta _{ij}=0\) se \(i\neq j\).

As quantidades:

\(I_{ij}=\sum m\left ( r^{2}\delta _{ij}-x_{i}x_{j} \right )\) (11)

são os momentos de inércia do sólido referidos ao referencial escolhido com origem no centro de massa. Constituem um tensor simétrico de 2ª ordem², i.e., são componentes de uma matriz real e simétrica. Como tal, é diagonalizável resolvendo a equação dos vetores próprios:

\(\sum_{j=1}^{3}I_{ij}e_{j}^{\left ( \lambda \right )}=I^{\left ( \lambda \right )}\;\; \; \; \; \lambda =1,2,3\)

Aqui, \(\lambda\) enumera os vetores e valores próprios. Recordamos os principais resultados:

a) Os três valores próprios são soluções da equação secular:

\(det\left ( \left [ I \right ]-I1 \right )=0\Leftrightarrow \begin{vmatrix} I_{11}-I & I_{12} & I_{13}\\ I_{21} & I_{22}-I & I_{23}\\ I_{31} & I_{32} & I_{33}-I \end{vmatrix}=0\)

(\(\mathbf{1}\) é a matriz unidade). Essas soluções são necessariamente reais e poderá haver degenerescência se duas ou mesmo as três forem iguais.

b) Vetores próprios correspondentes a valores próprios distintos são necessariamente ortogonais. No caso de degenerescências, podem sempre escolher-se ortogonais.

Assim:

\(\vec{e}^{\left ( \lambda \right )}\cdot \vec{e}^{\left ( \mu \right )}=\delta _{\lambda\mu}\; \; \; \; \; \; \; \; \; \; \lambda,\mu=1,2,3\)

Os valores próprios são designados por momentos principais de inércia e os vetores próprios definem as direções principais de inércia. Muitas vezes, estas direções são determinadas simplesmente por consideração de simetrias.

Há, evidentemente, vantagem em identificar os eixos do referencial CM com as direcções principais, i.e., \(\vec{e}_{1}=\vec{e}^{\left ( 1 \right )};\vec{e}_{2}=\vec{e}^{\left ( 2 \right )};\vec{e}_{3}=\vec{e}^{\left ( 3 \right )}\), que aceitaremos doravante. Nesta base, o tensor de inércia está diagonalizado, ficando muito simplificadas as expressões da energia de rotação, e do momento cinético de rotação, obtendo-se:

Energia de rotação: \(\frac{1}{2}\sum_{k=1}^{3}I^{\left ( k \right )}\omega _{k}^{2}\)

Momento cinético de rotação: \(\vec{L}_{G}=\sum_{k=1}^{3}I^{\left ( k \right )}\omega _{k}\vec{e}_{k}\) (12)

Podemos, finalmente, reescrever as eqs. (8) e (9):

\(K=\frac{1}{2}M\vec{V}_{G}^{2}+\frac{1}{2}\sum_{k=1}^{3}I^{\left ( k \right )}\omega _{k}^{2}\) (13)

\(\vec{L}_{O}=\vec{R}_{G}\wedge \vec{P}+\vec{L}_{G}\) (14)

Ficam aqui registadas as expressões dos momentos de inércia principais:

\(I^{\left ( 1 \right )}/\sum m\left ( x_{2}^{2}+x_{3}^{2} \right )\)

\(I^{\left ( 2 \right )}/\sum m\left ( x_{3}^{2}+x_{1}^{2} \right )\) (15)

\(I^{\left ( 3 \right )}/\sum m\left ( x_{1}^{2}+x_{2}^{2} \right )\)

Na prática, o teorema de Steiner revela-se muito útil para o cálculo de momentos de inércia. O teorema mostra que se \(I\) é o momento de inércia em relação a um eixo qualquer, não necessariamente principal, passando pelo centro de massa, e \(I′\) é o momento de inércia em relação a outro eixo paralelo ao primeiro à distância \(d\), então \(I'=I+Md^{2}\). A FIGURA 1 exemplifica o teorema.

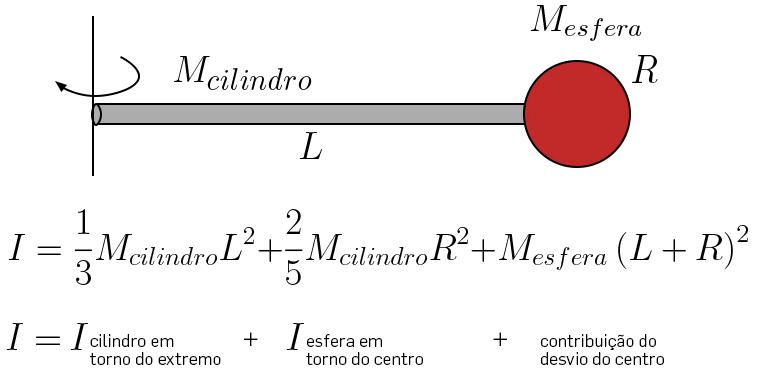
Exemplos de alguns momentos de inércia.

Em todos os exemplos que se seguem, supomos que a massa está uniformemente distribuída (FIGURA 1).

i) Esfera, raio \(R\) – há completa degenerescência:

\(I=\frac{2}{5}MR^{2}\) (16)

ii) Cilindro (Raio da base \(R\), altura \(h\) - o eixo do cilindro é direcção própria (eixo principal 3), onde se situa o centro de massa, a meia altura. Há dupla degenerescência:

\(I^{\left ( 3 \right )}\equiv I_{\left | \right |}=\frac{1}{2}MR^{2}\)

\(I^{\left ( 1 \right )}=I^{\left ( 2 \right )}\equiv I_{\bot}=\frac{1}{4}MR^{2}+\frac{1}{12}Mh^{2}\) (17)

iii) Paralelepípedo (arestas \(a,b,c\) paralelas, respectivamente, \(a\; \; \; x_{1},x_{2},x_{3}\)) – o centro de massa coincide com o centro do paralelepípedo (FIGURA 2).

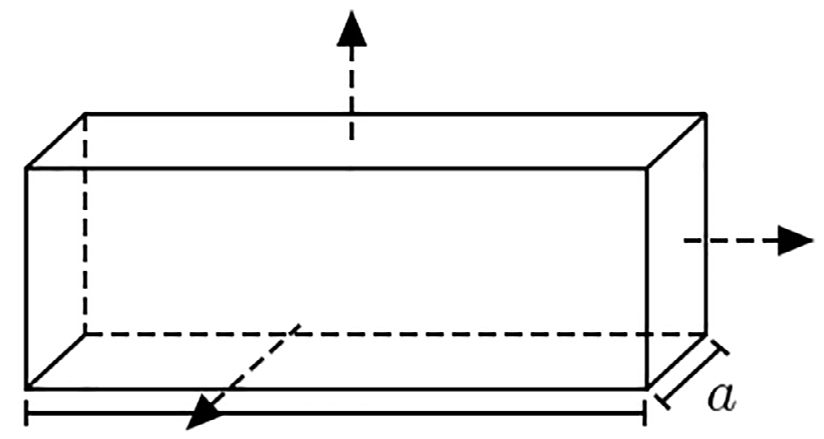
\(I^{\left ( 1 \right )}=\frac{M}{12}\left ( b^{2}+c^{2} \right )\)

\(I^{\left ( 2 \right )}=\frac{M}{12}\left ( c^{2}+a^{2} \right )\) (18)

\(I^{\left ( 3 \right )}=\frac{M}{12}\left ( a^{2}+b^{2} \right )\)

iv) Elipsóide (semieixos \(a,b,c\) paralelos, respectivamente, \(x_{1},x_{2},x_{3}\)) – o centro de massa coincide com o centro do elipsóide.

\(I^{\left ( 1 \right )}=\frac{M}{5}\left ( b^{2}+c^{2} \right )\)

\(I^{\left ( 2 \right )}=\frac{M}{5}\left ( c^{2}+a^{2} \right )\) (19)

\(I^{\left ( 3 \right )}=\frac{M}{5}\left ( a^{2}+b^{2} \right )\)

A esfera surge como um caso particular (\(a=b=c\equiv R\)). No caso de haver simetria de revolução em torno do eixo x3, por exemplo, é \(a=b\equiv R\), obtendo-se:

\(I^{\left ( 1 \right )}=I^{\left ( 2 \right )}\equiv I_{\bot}=\frac{M}{5}\left ( R^{2}+c^{2} \right )\)

\(I^{\left ( 3 \right )}=\equiv I_{\left | \right |}=\frac{2M}{5}R^{2}\) (20)

O caso \(c0\) representa uma esfera alongada na direção dos pólos.

Forças e seus momentos; equações de movimento

Cada partícula de um sólido rígido está submetida a dois tipos de forças: umas têm origem em fontes exteriores ao sólido, tal como o peso, e que designaremos por forças aplicadas, com a notação \(\vec{F}^{\left ( a \right )}\); as outras são forças internas, que notaremos por \(\vec{F}^{\left ( i \right )}\), e resultam da ação de uma partícula sobre outra mantendo o sólido rígido. Estas forças internas têm uma importante característica: considerando um par qualquer de partículas a força que uma partícula exerce sobre a outra tem a direção da linha que une as partículas e, pelo Terceiro Princípio de Newton, esta segunda partícula exerce sobre a primeira uma força igual e oposta (FIGURA 3). Por este motivo, a resultante das forças internas é nula, sendo também nulo o seu momento resultante com pólo arbitrário. E como a distância entre as partículas é fixa, as forças internas não realizam qualquer trabalho.

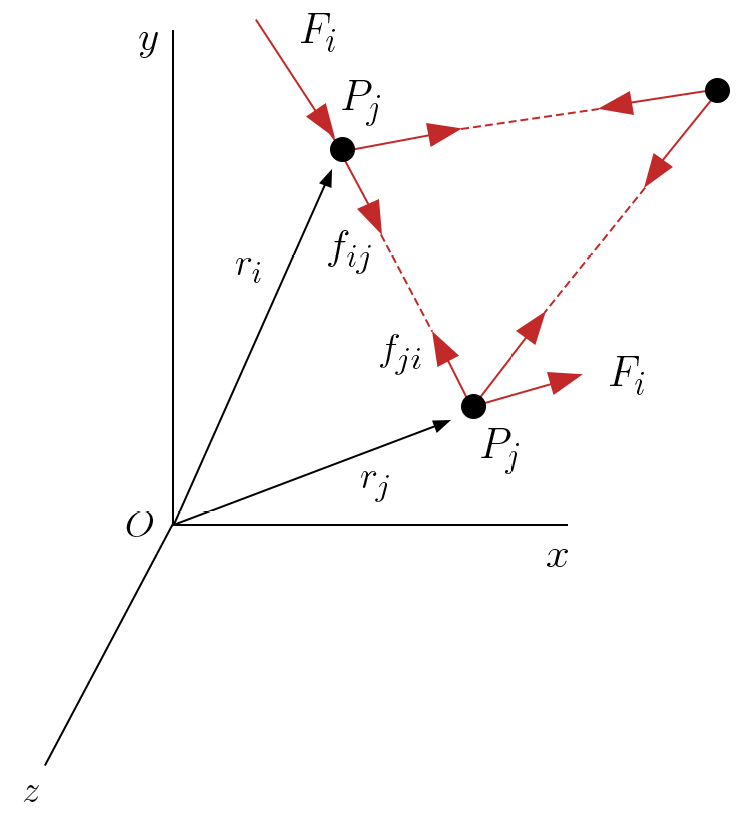
A equação de movimento para uma partícula é:

\(m\frac{d\vec{V}}{dt}=\vec{F}^{\left ( a \right )}+\vec{F}^{\left ( i \right )}\)

Somando sobre todas as partículas do sólido, obtem-se:

\(\sum m\frac{d\vec{V}}{dt}=\frac{d\vec{P}}{dt}=\sum \vec{F}^{\left ( a \right )}\) (21)

É, pois, a resultante das forças aplicadas que faz alterar a quantidade de movimento do sólido.

Consideremos, agora, o momento das forças que actuam sobre uma partícula. O pólo para o momento é a origem do referencial LAB. Tem-se:

\(\vec{M}_{O}=\vec{R}\wedge \left ( \vec{F}^{\left ( a \right )}+\vec{F}^{\left ( i \right )} \right )\)

Somando sobre todas as partículas, é eliminada a contribuição das forças internas, obtendo- se:

\(\vec{M}_{O}=\sum \vec{R}\wedge \vec{F}^{\left ( a \right )}=\vec{R}_{G}\wedge \sum \vec{F}^{\left ( a \right )}+\sum \vec{r}\wedge \vec{F}^{\left ( a \right )}\)

O momento é, assim, a soma do momento da resultante das forças aplicadas como se estivesse localizada no centro de massa, com o momento intrínseco, i.e., o momento das forças aplicadas em relação ao centro de massa. Ora, pelo teorema dos momentos cinéticos, é:

\(\vec{M}_{O}=\frac{d}{dt}\vec{L}_{O}=\vec{R}_{G}\wedge \frac{d}{dt}\vec{P}+\frac{d}{dt}\vec{L}_{G}=\vec{R}_{G}\wedge \sum \vec{F}^{\left ( a \right )}+\frac{d}{dt}\vec{L}_{G}\)

onde se usaram as eqs. (9) e (21). Comparando com o resultado anterior, vem:

\(\frac{d}{dt}\vec{L}_{G}=\sum \vec{r}\wedge \vec{F}^{\left ( a \right )}\) (22)

O momento cinético intrínseco evolui por ação do momento das forças aplicadas em relação ao centro de massa.

As equações (21) e (22), projetadas em qualquer sistema de eixos, originam seis equações que determinam a dinâmica dos seis graus de liberdade do sólido. Elas separam completamente o movimento do centro de massa do movimento de rotação em torno do centro de massa. Aquele, comporta-se como uma partícula material (com a massa do sólido), enquanto este exibe uma dinâmica muito mais rica. Quando observamos um planeta distante, é o movimento do centro de massa que é descrito; quando detetamos as ondas de rádio que nos chegam de um pulsar (estrela de neutrões), obtemos informação sobre a dinâmica da sua rotação.

Potência das forças e trabalho virtual

Como referido atrás, as forças internas não realizam qualquer trabalho. Calculemos, então, a potência das forças aplicadas:

\(P=\sum \vec{F}^{\left ( a \right )}\cdot \vec{V}=\sum \vec{F}^{\left ( a \right )}\cdot \left ( \vec{V}_{G}+\vec{\omega }\wedge \vec{r} \right )=\left ( \sum \vec{F}^{\left ( a \right )} \right )\cdot \vec{V}_{G}+\vec{\omega }\cdot \left ( \sum \vec{r}\wedge \vec{F}^{\left ( a \right )} \right )\) (23)

Esta expressão mostra a decomposição da potência das forças aplicadas em duas parcelas, uma apenas envolvendo a resultante e a velocidade do centro de massa, a outra envolvendo o momento resultante intrínseco e a velocidade de rotação.

Usando as eqs. (21) e (22), obtemos:

\(P=\vec{V}_{G}\cdot \frac{d\vec{P}}{dt}+\vec{\omega }\cdot \frac{d\vec{L}_{G}}{dt}\)

Invocando agora as eqs. (3) e (12), obtemos:

\(P=\frac{d}{dt}\left ( \frac{1}{2}M\vec{V}_{G}^{2} \right )+\vec{\omega }\cdot \frac{d}{dt}\left ( \sum_{k=1}^{3}I^{\left ( k \right )}\omega _{k}\vec{e}_{k} \right )=\frac{d}{dt}\left ( \frac{1}{2}M\vec{V}_{G}^{2} \right )+\frac{d}{dt}\left ( \sum_{k=1}^{3}I^{\left ( k \right )}\omega _{k}^{2} \right )-\sum_{k=1}^{3}I^{\left ( k \right )}\omega _{k}\vec{e}_{k}\cdot \frac{d\vec{\omega }}{dt}\)

Ora:

\(\frac{d\vec{\omega }}{dt}=\frac{d}{dt}\left ( \sum_{k=1}^{3}w_{k}\vec{e}_{k} \right )=\sum_{k=1}^{3}\left ( \frac{d\omega _{k}}{dt}\vec{e}_{k}+\omega _{k}\frac{d\vec{e}_{k}}{dt} \right )=\sum_{k=1}^{3}\left ( \frac{d\omega _{k}}{dt}\vec{e}_{k}+\omega _{k}\vec{\omega }\wedge \vec{e}_{k} \right )\)

Substituindo na equação anterior e recordando a ortogonalidade da base CM, resulta:

\(P=\frac{d}{dt}\left ( \frac{1}{2}M\vec{V}_{G}^{2} \right )+\vec{\omega }\cdot \frac{d}{dt}\left ( \sum_{k=1}^{3}I^{\left ( k \right )}\omega _{k}\vec{e}_{k} \right )=\frac{d}{dt}\left ( \frac{1}{2}M\vec{V}_{G}^{2} \right )+\frac{d}{dt}\left ( \frac{1}{2}\sum_{k=1}^{3}I^{\left ( k \right )}\omega _{k}^{2} \right )\) (24)

Vemos aqui a conservação da energia mecânica: o trabalho realizado na unidade de tempo pelas forças aplicadas (i.e. a potência) distribui-se pelo aumento, na unidade de tempo, das energias cinéticas de rotação e translação.

Regressemos à eq. (23) e multipliquemos ambos os membros por \(\delta t\), um pequeno intervalo de tempo. Fica:

\(\delta W=P\delta t\left ( \sum \vec{F}^{\left ( a \right )} \right )\cdot \delta \vec{R}_{G}+\left ( \sum \vec{r}\wedge \vec{F}^{\left ( a \right )} \right )\cdot \delta \vec{\Omega }\) (25)

Aqui, \(\delta W\) é o trabalho infinitesimal realizado pelas forças aplicadas: ele distribui-se pelo trabalho da resultante das forças aplicadas para uma translação do sólido e pelo trabalho do momento das forças aplicadas para uma rotação infinitesimal do sólido (ver eq. (5)). Mas a eq. (25) é mais geral do que a sua dedução apresenta, porque podemos imaginar para qualquer sistema, mesmo não mecânico, uma translação ou uma rotação como se tal sistema se comportasse como um sólido rígido. Nessas condições, \(\delta W\) designa-se por trabalho virtual sobre o sistema realizado pelas forças a ele aplicadas e o segundo membro da eq. (25) permite-nos, então, obter a resultante das forças aplicadas, imaginando uma pequena translação, e o momento resultante das mesmas forças, imaginando uma pequena rotação. Este método dos trabalhos virtuais tem um âmbito de aplicação muito vasto, abrangendo praticamente toda a Física.

As equações de Euler

Um sólido rígido projetado no campo gravítico da Terra, tem um comportamento muito mais variado do que o de uma partícula material. É certo que o seu centro de massa movimenta- se exatamente como uma partícula (ver eq. (21)), mas o sólido pode rodar enquanto se move, exibindo desse modo uma maior variedade de comportamentos. Para um campo gravítico uniforme, e ignorando a força de Coriolis² que em qualquer caso é uma pequena correção, a rotação do sólido é regida pela eq. (22) com o segundo membro nulo, pois que é nulo o momento do peso em relação ao centro de massa – o sólido roda livremente. Assim, usando a eq. (12), tem-se:

\(\frac{d}{dt}\left ( \sum_{k=1}^{3}I^{\left ( k \right )}\omega _{k}\vec{e}_{k} \right )=\sum_{k=1}^{3}I^{\left ( k \right )}\left ( \frac{d\omega _{k}}{dt}\vec{e}_{k}+\omega _{k}+\omega _{k}\frac{d\vec{e}_{k}}{dt} \right )=\sum_{k=1}^{3}I^{\left ( k \right )}\left ( \frac{dt}{d\omega k}\vec{e}_{k}+\omega _{k}\vec{\omega }\wedge \vec{e}_{k} \right )=0\)

Projetando nos eixos principais de inércia, obtemos as equações de Euler para o sólido livre:

\(I^{\left ( 1 \right )}\frac{d\omega _{1}}{dt}+\left ( I^{\left ( 3 \right )}-I^{\left ( 2 \right )} \right )\omega _{2}\omega _{3}=0\)

\(I^{\left ( 2 \right )}\frac{d\omega _{2}}{dt}+\left ( I^{\left ( 1 \right )}-I^{\left ( 3 \right )} \right )\omega _{1}\omega _{3}=0\) (26)

\(I^{\left ( 3 \right )}\frac{d\omega _{3}}{dt}+\left ( I^{\left ( 2 \right )}-I^{\left ( 1 \right )} \right )\omega _{2}\omega _{1}=0\)

Vários resultados interessantes são agora apresentados.

i) Se o vector rotação instantânea estiver alinhado com um eixo próprio (por exemplo, \(\omega _{2}=\omega _{3}=0\), assim permanecerá sempre, mantendo-se o sólido a rodar em torno desse eixo. Também no caso de completa degenerescência dos momentos de inércia principais (i.e., todos iguais), o sólido roda em torno da direcção inicialmente fixada, como acontece com uma bola ou um cubo.

ii) Admitamos que \(I^{\left ( 1 \right )}\)<\(I^{\left ( 2 \right )}\)<\(I^{\left ( 3 \right )}\), como é o caso de um paralelepípedo com arestas desiguais (ver eq. (18)) e estudemos a estabilidade das rotações efetuadas próximas, mas não coincidentes, com cada um dos eixos principais.

Suponhamos, então, que \(\omega _{1}=\Omega +\delta \omega _{1}\), com \(\delta \omega _{1},\omega _{2},\omega _{3}\) muito menores que \(\Omega \). A primeira equação em (26) mostra que \(\delta \omega _{1}\) é de segunda ordem nos pequenos acréscimos – a rotação dominante faz-se em torno de \(\omega _{1}\) com a frequência \(\Omega \). Quanto às segunda e terceira equações, reescrevemo-las:

\(I^{\left ( 2 \right )}\frac{d\omega _{2}}{dt}-\left ( I^{\left ( 3 \right )}-I^{\left ( 1 \right )} \right )\omega _{3}\Omega \approx 0\)

\(I^{\left ( 3 \right )}\frac{d\omega _{3}}{dt}-\left ( I^{\left ( 2 \right )}-I^{\left ( 1 \right )} \right )\omega _{2}\Omega \approx 0\)

Donde:

\(\frac{d^{2}\omega _{2}}{dt^{2}}+\frac{\left ( I^{\left ( 3 \right )}-I^{\left ( 1 \right )} \right )\left ( I^{\left ( 2 \right )}-I^{\left ( 1 \right )} \right )}{I^{\left ( 2 \right )}I^{\left ( 3 \right )}}\Omega ^{2}\omega _{2}\approx 0\)

É a equação de um oscilador harmónico com a frequência natural \(\Omega\sqrt{\frac{\left ( I^{\left ( 3 \right )}-I^{\left ( 1 \right )}\left ( I^{\left ( 2 \right )}-I^{\left ( 1 \right )} \right ) \right )}{I^{\left ( 2 \right )}I^{\left ( 3 \right )}}}\). O mesmo acontece com \(\omega_{3}\). Estas componentes permanecem pequenas e a rotação efectua-se primordialmente em torno de \(x_{1}\), com pequenas oscilações deste eixo. Quer dizer, a rotação em torno de \(x_{1}\) é estável.

O mesmo procedimento aplicado a uma rotação em torno de \(x_{3}\) conduz à mesma conclusão, embora com diferente frequência do “oscilador harmónico”.

O que se passa com o segundo eixo? Procedendo como antes, fazemos \(\omega _{2}=\Omega +\delta \omega _{2}\), com \(\delta \omega _{2},\omega _{1},\omega _{3}\) muito menores que \(\Omega\). Obtemos, da primeira e terceira equação em (26):

\(I^{\left ( 1 \right )}\frac{d\omega _{1}}{dt}+\left ( I^{\left ( 3 \right )}-I^{\left ( 2 \right )} \right )\Omega\omega_{3}\simeq 0\)

\(I^{\left ( 3 \right )}\frac{d\omega _{3}}{dt}+\left ( I^{\left ( 2 \right )}-I^{\left ( 1 \right )} \right )\Omega\omega_{1}\simeq 0\)

Donde:

\(\frac{d^{2}\omega_{1}}{dt^{2}}-\frac{\left ( I^{\left ( 3 \right )}-I^{\left ( 2 \right )} \right )\left ( I^{\left ( 2 \right )}-I^{\left ( 1 \right )} \right )}{I^{\left ( 1 \right )}I^{\left ( 3 \right )}}\Omega^{2}\omega_{1}\approx 0\)

A mesma equação é obtida para \(\omega_{3}\). As soluções são proporcionais a \(e^{\pm \alpha t}\), com \(\alpha=\Omega\sqrt{\frac{\left ( I^{\left ( 3 \right )}-I^{\left ( 2 \right )} \right )\left ( I^{\left ( 2 \right )}-I^{\left ( 1 \right )} \right )}{I^{\left ( 1 \right )}I^{\left ( 3 \right )}}}\). Para condições iniciais genéricas, haverá sempre crescimento no tempo: as rotações em torno do eixo \(x_{2}\) são instáveis! Este eixo está associado com o momento de inércia de valor intermediário. Para um paralelepípedo como na FIGURA 2, este eixo é perpendicular às faces com a menor e maior arestas (ver eq. (18)). Assim, quando atiramos um livro introduzindo-lhe rotação, esta será instável quando o eixo de rotação for perpendicular à lombada do livro que, em geral, é a que se apresenta nas condições indicadas. Rotações em torno dos eixos perpendiculares à face larga da capa ou ao topo do livro são estáveis.

iii) Um pião a girar tem uma grande variedade de movimentos que não cabe aqui analisar na totalidade. Iremos, apenas, considerar um pião simétrico mantendo fixo o seu ponto de contacto com um plano horizontal. Admitidos realizadas as condições que permitem que também se mantenha fixo o ângulo \(\theta\) que o seu eixo de simetria faz com a vertical (tal acontece para rápidas rotações). Esse eixo é um eixo de simetria que identificaremos com o eixo principal \(x_{3}\). Interessa, aqui, considerar o ponto fixo para origem \(O\) do referencial ligado ao sólido e designaremos por \(I_{\left | \right |}\) e \(I_{\bot}\) os momentos de inércia em relação respectivamente ao eixo de simetria e a qualquer eixo perpendicular àquele passando pelo ponto fixo. Sendo \(\Omega\) a velocidade de rotação em torno do eixo do pião, então \(\vec{L}_{O}=I_{\left | \right |}\Omega\vec{e}_{3}\) e, pelo teorema dos momentos cinéticos, obtem-se:

\(\frac{d\vec{L}_{O}}{dt}=\vec{M}_{O}^{\left ( a \right )}\)

Só há duas forças aplicadas: o peso e a reação do plano horizontal localizada no ponto fixo. Mas esta, pela sua localização, tem momento nulo. Quanto ao peso, está aplicado no centro de massa situado no eixo de simetria, à distância \(l\) do ponto fixo, contribuindo com o momento −\(-Mgl\vec{e}_{3}\wedge \vec{e}_{z}\), onde \(\vec{e}_{z}\) é o versor da vertical, independente do tempo. Assim, a equação anterior fica:

\(I_{\left | \right |}\Omega\frac{d\vec{e}_{3}}{dt}=Mgl\vec{e}\wedge \vec{e}_{3}\) (27)

Notemos que \(\theta\) é o ângulo entre os versores \(\vec{e}_{3}\) e \(\vec{e}_{z}\). Qual o significado desta equação? Começamos por observar que o vetor no segundo membro da eq. (27) é horizontal e tem grandeza \(sen\theta\). Então, num curto intervalo de tempo \(\delta t\) o versor \(\vec{e}_{3}\) é acrescido de \(\delta \vec{e}_{3}=\frac{Mgl}{I_{\left | \right |}\Omega}\vec{e}_{3}\delta t\), acréscimo que é horizontal e perpendicular ao versor original \(\vec{e}_{3}\), de modo que este mantem a sua grandeza unitária. Quer dizer, naquele curto intervalo de tempo, o versor \(\vec{e}_{3}\) rodou na horizontal do ângulo \(\delta \alpha=\frac{Mglsen\theta}{I_{\left | \right |}}|Omega\delta t\). Passados outros \(\delta t\) segundos, outra rotação do mesmo ângulo, e assim sucessivamente. Esta acumulação de acréscimos no ângulo de rotação totaliza \(2\pi\) ao fim de um período \(T=2\pi\frac{I_{\left | \right |}\Omega }{Mglsen\theta}\), i.e., a frequência desta precessão do eixo do pião é \(\omega=\frac{Mglsen\theta}{I_{\left | \right |}\Omega}\). A eq. (27) tipifica um movimento de precessão e o resultado obtido para a frequência de precessão é facilmente adaptado a outras situações onde aquele movimento ocorre.

iv) A Terra tem a forma de um elipsóide ligeiramente achatado nos pólos. O eixo do elipsóide não coincide com o eixo de rotação: subtendem um angulo \(\theta=23,5^{o}\). Daqui decorrem duas consequências: mesmo que não existam momentos aplicados, conservando-se, pois, \(\vec{L}_{G}\), o eixo de rotação efetua uma precessão em torno do eixo de simetria – o estudo desta precessão é aqui estudado. Mas existem forças aplicadas, originando um momento, devidas às não uniformes forças de atração gravitacionais quer do Sol quer da Lua – essa precessão, com período de cerca de 30.000 anos, é de análise mais complexa, não sendo aqui considerada.

Na ausência de momentos aplicados, as equações de Euler (ver (26)) serão usadas com as seguintes adaptações: o eixo do elipsóide será tomado como eixo \(x_{3}\), admitindo um momento de inércia \(I_{\left | \right |}\). Os outros dois eixos são escolhidos arbitrariamente no plano perpendicular ao eixo de simetria e \(I\not\) designa o momento de inércia em relação a qualquer um deles. Nestas condições, as equações de Euler escrevem-se:

\(I_{\bot}\frac{d\omega _{1}}{dt}+\left ( I_{\left | \right |}-I_{\bot} \right )\omega _{2}\omega _{3}=0\)

\(I_{\bot}\frac{d\omega _{2}}{dt}+\left ( I_{\bot}-I_{\left | \right |} \right )\omega _{1}\omega _{3}=0\)

\(I^{\left ( 3 \right )}\frac{d\omega_{3}}{dt}=0\; \; \; \rightarrow \; \; \; \omega=\Omega\)

É, pois, constante a componente do vector rotação instantânea segundo o eixo de simetria, devendo ser \(\Omega=\omega_{R}cos\theta\), com \(\omega_{R}=2\pi\)/ dia. As outras duas equações reduzem- -se, para cada componente, à equação de um oscilador harmónico, estando desfasadas de \(\frac{\pi}{2}\):

\(\frac{d^{2}\omega_{1}}{dt^{2}}+\left ( \frac{I_{\left | \right |}-I_{\bot}}{I_{\bot}} \right )\Omega^{2}\omega_{1}=0\)

Quer dizer, a projecção do vector rotação instantânea no plano perpendicular ao eixo de simetria, roda com a frequência \(\omega=\left ( \frac{I_{_{\left | \right |}}-I_{\bot}}{I_{\bot}} \right )\Omega\). Para a Terra, \( \frac{I_{_{\left | \right |}}-I_{\bot}}{I_{\bot}} \simeq \frac{1}{300}\), obtendo-se um período de precessão de 327 dias, aproximadamente, muito próximo do valor observado de cerca de 430 dias³.

v) O pêndulo composto

O pêndulo simples, sendo um dos mais elementares “relógios”⁴, tem o inconveniente de ser muito suscetível a perturbações externas, tais como humidade ou temperatura, que alteram o seu comprimento e afetam o seu regular funcionamento. O pêndulo composto é muito mais estável a essas perturbações e faz parte integrante dos “relógios de pé” muito usados em séculos passados. A FIGURA 5 exibe a componente essencial de um pêndulo composto, preparado para várias experiências que facilmente podem ser implementadas em laboratórios. Trata-se de uma régua (massa \(M\), comprimento \(l\)) com uma série de furos equidistantes ao longo da régua por onde se pode suspender num eixo horizontal. Designamos por \(h\) a distância do centro de massa (a meio da régua) ao eixo horizontal e por \(theta\) o ângulo da régua com a vertical, contado a partir deste e no sentido antihorário (direto). Tomando o ponto de fixação como origem do LAB, o teorema dos momentos cinéticos fornece a equação do movimento, notando que apenas o peso gera um momento neste pólo:

\(I\frac{d^{2}\theta}{dt^{2}}=-Mghsen\theta\)

O momento de inércia \(I\) em relação ao eixo horizontal é facilmente calculável usando o teorema de Steiner:

\(I=\frac{Ml^{2}}{12}+Mh^{2}\)

A equação de movimento é idêntica à de um pêndulo simples. Para pequenas oscilações (\(sen\theta\approx \theta\)), reduz-se à de um oscilador harmónico⁵, obtendo-se, assim, o período do movimento:

\(T=2\pi\sqrt{\frac{\frac{l^{2|}}{12}+h^{2}}{gh}}\)

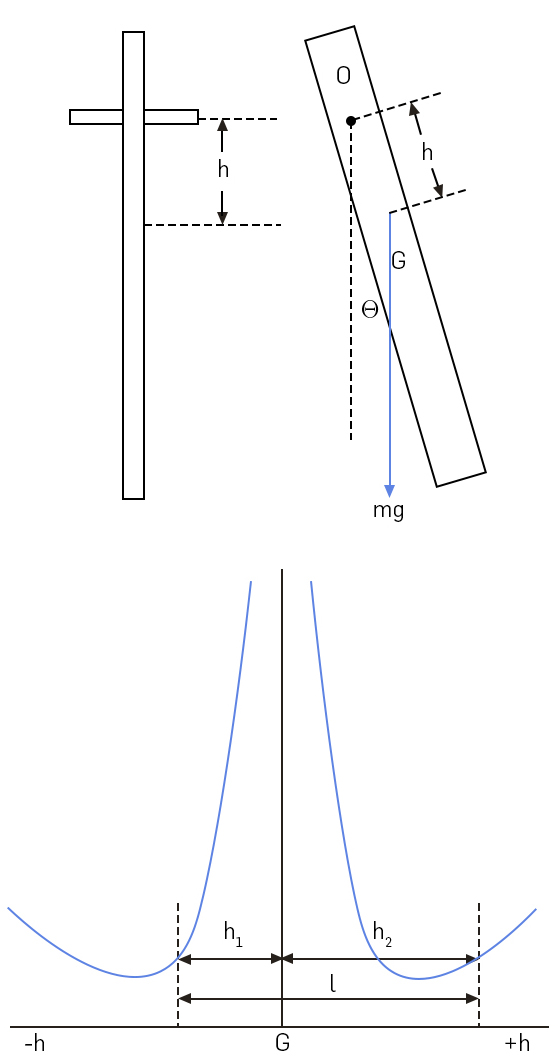
É fácil ver que a função \(T(h)\) passa por um mínimo e não deve surpreender a divergência para \(h=0\) pois que, em tal caso, o eixo de sustentação passa pelo centro de massa. Esta função está representada na parte inferior da FIGURA 5 (os valores negativos de \(h\) apenas representam pontos de sustentação simetricamente colocados em relação ao centro de massa).

vi) O giroscópio de Foucault

Em 1852, Léon Foucault apresentou uma sua invenção, o giroscópio (FIGURA 6), um aparelho puramente mecânico que aproveita a rotação da Terra para indicar a direção Norte (geográfico). O giroscópio consiste num disco capaz de se orientar no espaço, posto a girar com uma velocidade de rotação uniforme (em grandeza) através de um motor; o eixo desta rotação passa pelo centro de massa do disco, de modo a garantir que o momento do peso, em CM, é nulo. A precessão do eixo deve-se ao momento das forças de Coriolis⁶ e depende, pois, do movimento de rotação da Terra. A análise do comportamento dinâmico do giroscópio é bastante laboriosa e extensa pelo que não será apresentada aqui. Mas é fácil perceber o princípio do funcionamento com o seguinte modelo simples: uma esfera em rotação livre no espaço (sem qualquer ponto de apoio). Designando por \(\vec{\omega}\) o seu vetor rotação instantânea, então o momento cinético intrínseco é \(\vec{L}_{G}=I\vec{\omega}\), onde \(I\) é o momento de inércia em relação a qualquer eixo passando pelo centro de massa. Sobre cada elemento de massa \(dm\) atua, apenas, a força de Coriolis (porque a Terra não é um referencial de inércia): \(-2dm\vec{\omega}_{T}\wedge \vec{\nu }\), com \(\vec{\omega}_{T}\) vetor rotação instantânea da Terra e \(\vec{\nu }\) velocidade do elemento de massa em relação a LAB (na Terra).

Ora, para uma rotação da esfera é \(\vec{\nu }=\vec{\omega}\wedge \vec{r}\). Deste modo, temos:

\(\vec{M}_{G}=\int dm\vec{r}\wedge \left ( -2\vec{\omega }_{T}\wedge \vec{\nu} \right )=2\int dm\left ( \vec{\omega }\wedge \vec{r} \right )\left ( \vec{\omega }\cdot \vec{r} \right )=I\vec{\omega}\wedge \vec{\omega_{T}}\)

Assim:

\(\frac{d\vec{L}_{G}}{dt}=\vec{M}_{G}\rightarrow \frac{d\vec{\omega}}{dt}=\vec{\omega}\wedge \vec{\omega}_{T}\)

O vetor rotação instantânea da esfera precessa em torno do eixo de rotação da Terra, indicando, dessa forma, a direção do Norte geográfico.